La distribution binomiale

Introduction aux statistiques en Python

Maggie Matsui

Content Developer, DataCamp

Jeu de pile ou face

Pile ou face avec un côté H avec 50 % de chances, l’autre côté T avec 50 % de chances

Introduction aux statistiques en Python

Résultats binaires

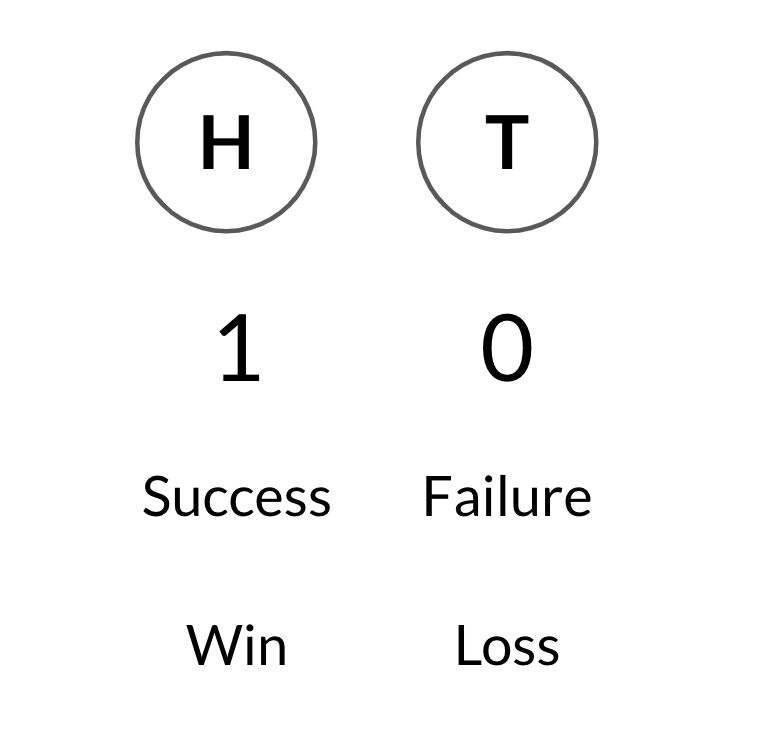
H et T, 1 et 0, réussite et échec, victoire et défaite

Introduction aux statistiques en Python

Lancer une seule pièce

binom.rvs(nombre de pièces, probabilité de face/réussite, size=nombre d'essais)

1 = face, 0 = pile

from scipy.stats import binom

binom.rvs(1, 0.5, size=1)

array([1])
Introduction aux statistiques en Python

Lancer une seule pièce, plusieurs fois

binom.rvs(1, 0.5, size=8)

array([0, 1, 1, 0, 1, 0, 1, 1])

 

binom.rvs(1, 0.5, 8) avec 1 en rouge, 0.5 en jaune, 8 en bleu. Texte : Lancer 1 (en rouge) pièce avec 50 % (en jaune) de chances de succès, 8 (en bleu) fois

Introduction aux statistiques en Python

Lancer plusieurs pièces, une seule fois

binom.rvs(8, 0.5, size=1)

array([5])

 

binom.rvs(8, 0.5, size=1) avec 8 en rouge, 0.5 en jaune, 1 en bleu. Texte : Lancer 8 (en rouge) pièces avec 50 % (en jaune) de chances de succès 1 (en bleu) fois

Introduction aux statistiques en Python

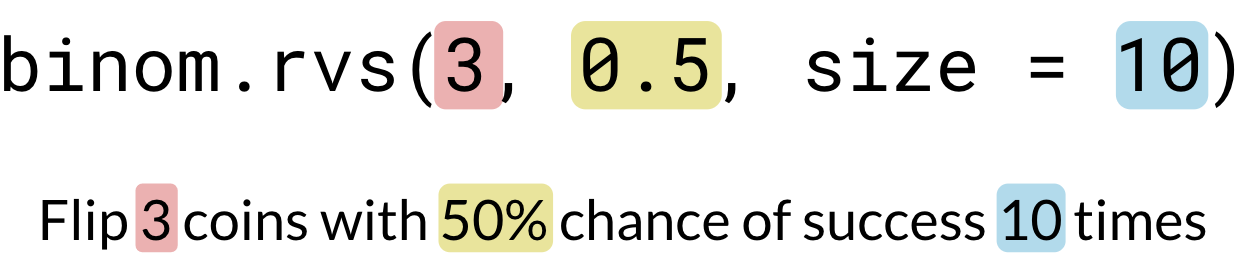
Lancer plusieurs pièces, plusieurs fois

binom.rvs(3, 0.5, size=10)

array([0, 3, 2, 1, 3, 0, 2, 2, 0, 0])

 

binom.rvs(3, 0.5, size=10) avec 3 en rouge, 0,5 en jaune, 10 en bleu. Texte : Lancer une pièce 3 (en rouge) fois avec 50 % (en jaune) de chances de succès 10 (en bleu) fois

Introduction aux statistiques en Python

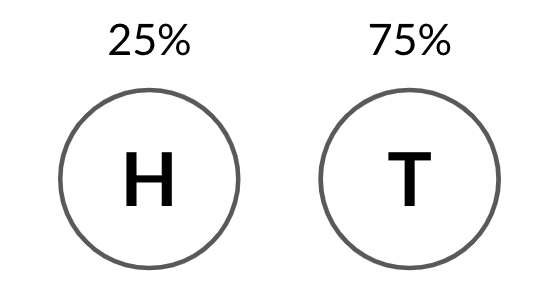
Autres probabilités

binom.rvs(3, 0.25, size=10)

array([1, 1, 1, 1, 0, 0, 2, 0, 1, 0])

 

Image de face avec une probabilité de 25 % et de pile avec une probabilité de 75 %

Introduction aux statistiques en Python

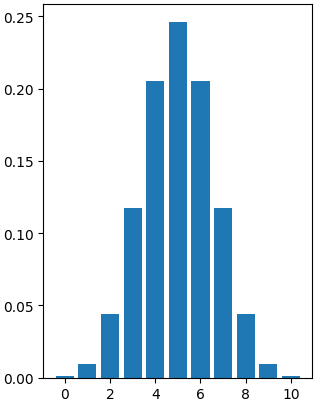
Distribution binomiale

Distribution de probabilité du nombre de réussites dans une séquence d’essais indépendants

Par exemple, nombre de faces dans une séquence de tirages à pile ou face

Décrite par $n$ et $p$.

  • $n$ : nombre total d’essais
  • $p$ : probabilité de réussite
binom.rvs(n=10, p=0.5, size=20)

Graphique de la distribution binomiale avec n=10, p = 0,5

Introduction aux statistiques en Python

Quelle est la probabilité d’obtenir 7 faces ?

$P(\text{nombre de faces} = 7)$

# binom.pmf(num heads, num trials, prob of heads)
binom.pmf(7, 10, 0.5)

0.1171875
Introduction aux statistiques en Python

Quelle est la probabilité d’obtenir au plus 7 faces ?

$P(\text{nombre de faces} \le 7)$

binom.cdf(7, 10, 0.5)

0.9453125
Introduction aux statistiques en Python

Quelle est la probabilité d’obtenir plus de 7 faces ?

$P(\text{nombre de faces} > 7)$

1 - binom.cdf(7, 10, 0.5)

0.0546875
Introduction aux statistiques en Python

Valeur attendue

$\text{valeur attendue} = n \times p$

Nombre attendu de faces sur 10 lancers $= 10 \times 0,5 = 5$.

Introduction aux statistiques en Python

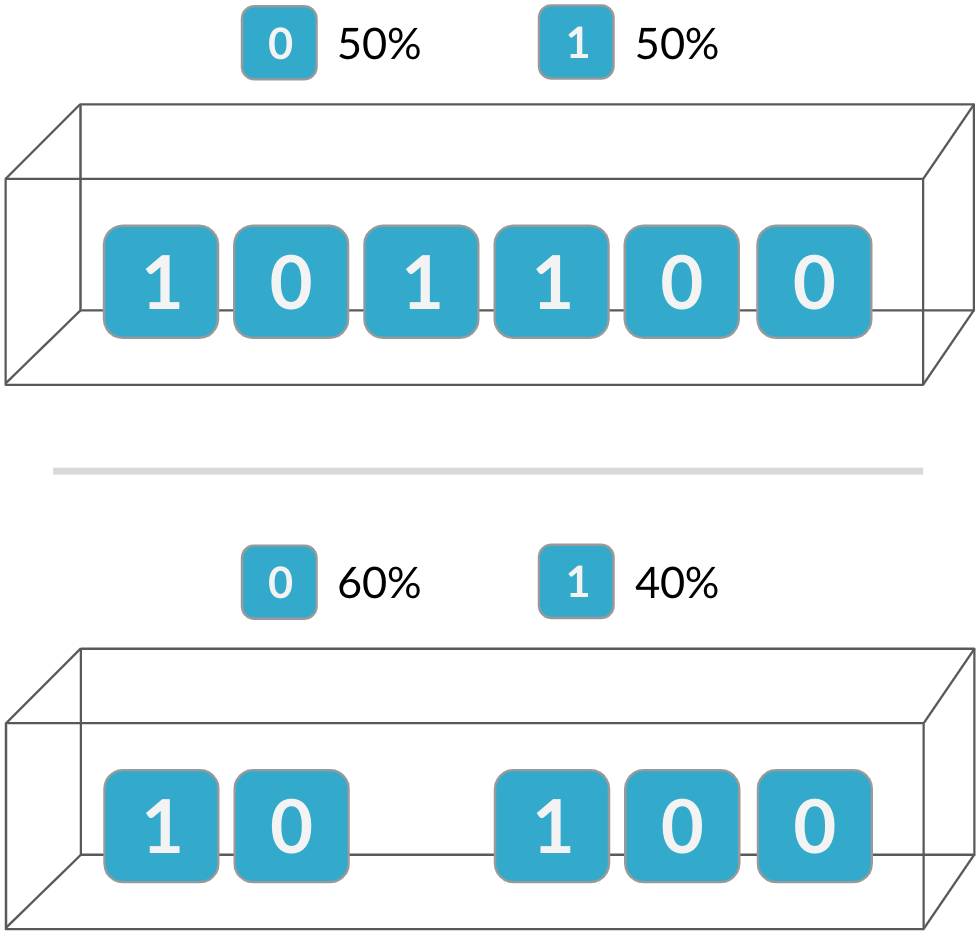
Indépendance

La distribution binomiale est une distribution de probabilité du nombre de réussites dans une séquence d’essais indépendants.

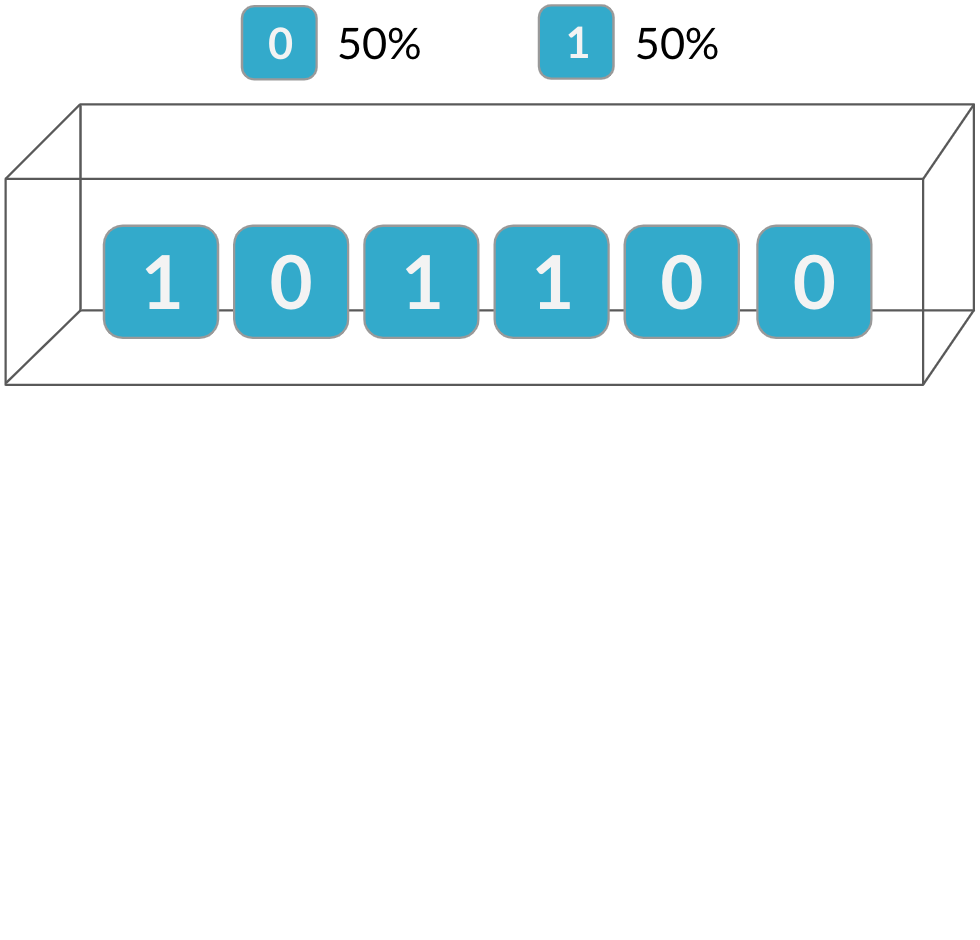
Boîte de billets avec 3 zéros et 3 uns. 50 % de chances de 0, 50 % de chances de 1

Introduction aux statistiques en Python

Indépendance

La distribution binomiale est une distribution de probabilité du nombre de réussites dans une séquence d’essais indépendants.

 

Les probabilités du deuxième essai sont modifiées par le résultat du premier.

 

Si les essais ne sont pas indépendants, la distribution binomiale ne s’applique pas.

Boîte de billets avec 3 zéros et 2 uns. 60 % de chances de 0, 40 % de chances de 1

Introduction aux statistiques en Python

Passons à la pratique !

Introduction aux statistiques en Python

Preparing Video For Download...