Mesures de dispersion

Introduction aux statistiques en Python

Maggie Matsui

Content Developer, DataCamp

Qu’est-ce que la dispersion ?

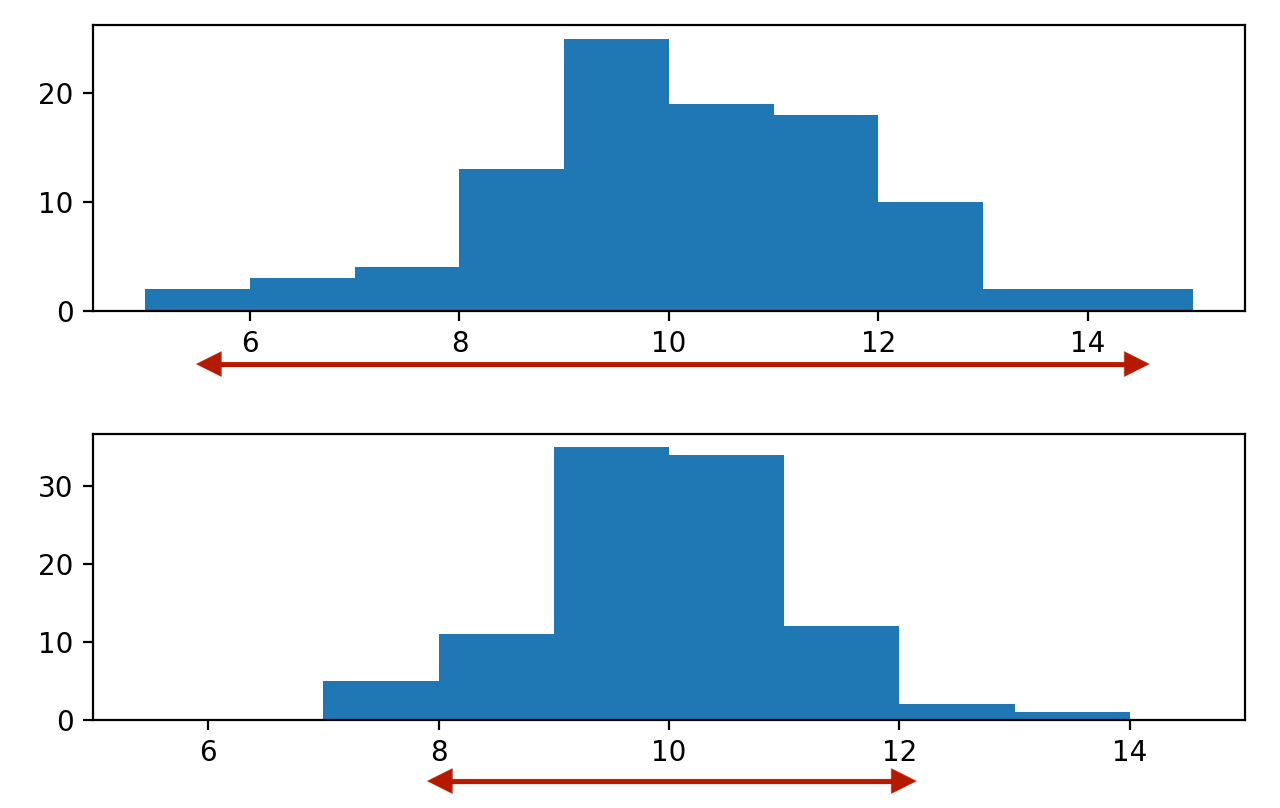
Deux histogrammes : l'un étroit avec des données ne couvrant que quelques valeurs, l’autre plus large avec des données couvrant davantage de valeurs.

Introduction aux statistiques en Python

Variance

Distance moyenne entre chaque point de données et la moyenne des données

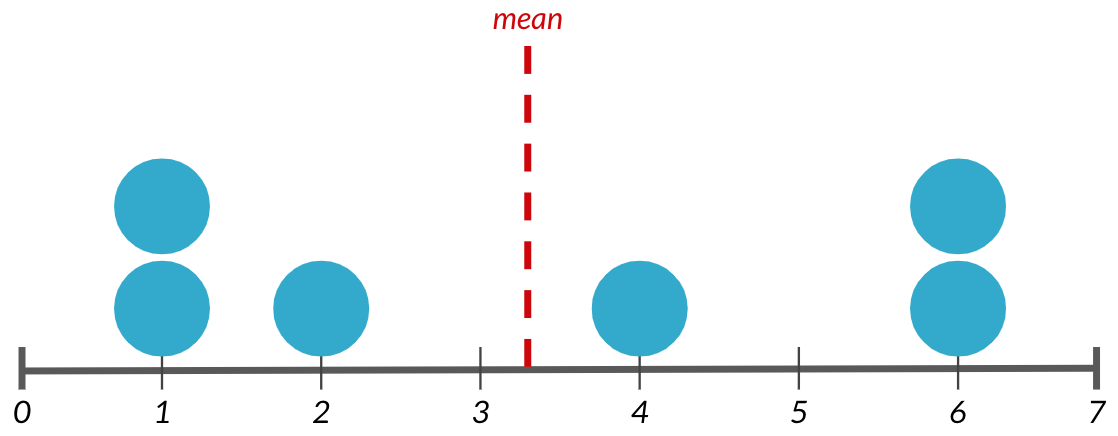
Un graphique de 7 points de données avec une ligne rouge au milieu représentant la moyenne.

Introduction aux statistiques en Python

Variance

Distance moyenne entre chaque point de données et la moyenne des données

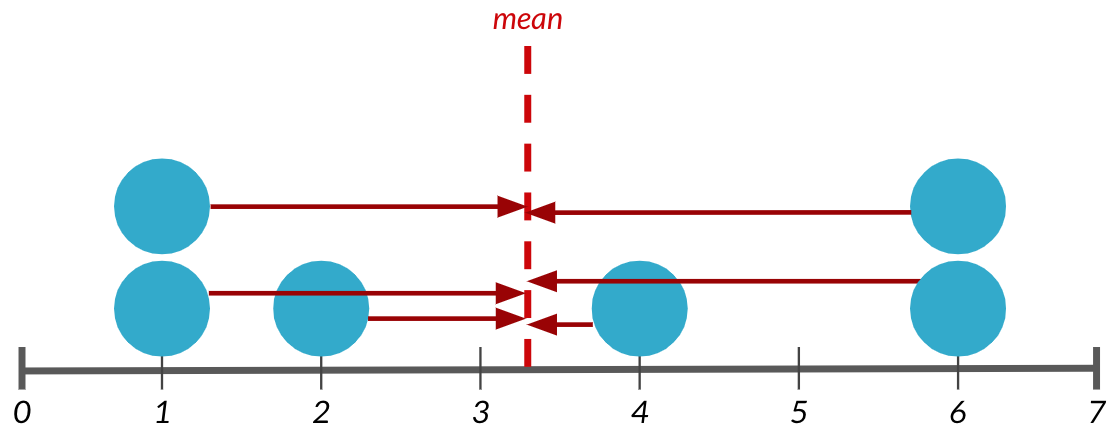
Un graphique de 7 points de données avec une ligne rouge au milieu représentant la moyenne. Des flèches sont tracées entre chaque point et la ligne moyenne.

Introduction aux statistiques en Python

Calcul de la variance

1. Soustrayez la moyenne de chaque point de données

dists = msleep['sleep_total'] - 
        np.mean(msleep['sleep_total'])
print(dists)

0     1.666265
1     6.566265
2     3.966265
3     4.466265
4    -6.433735
      ...

2. Mettez chaque distance au carré

sq_dists = dists ** 2
print(sq_dists)

0      2.776439
1     43.115837
2     15.731259
3     19.947524
4     41.392945
      ...
Introduction aux statistiques en Python

Calcul de la variance

3. Faites la somme des distances au carré

sum_sq_dists = np.sum(sq_dists)
print(sum_sq_dists)

1624.065542

4. Divisez par le nombre de points de données - 1

variance = sum_sq_dists / (83 - 1)
print(variance)

19.805677

Utilisez np.var()

np.var(msleep['sleep_total'], ddof=1)

19.805677

Sans ddof=1, la variance de la population est calculée au lieu de la variance de l’échantillon :

np.var(msleep['sleep_total'])

19.567055
Introduction aux statistiques en Python

Écart-type

np.sqrt(np.var(msleep['sleep_total'], ddof=1))

4.450357

np.std(msleep['sleep_total'], ddof=1)

4.450357
Introduction aux statistiques en Python

Écart moyen absolu

dists = msleep['sleep_total'] - np.mean(msleep['sleep_total'])

np.mean(np.abs(dists))

3.566701

Écart-type et écart moyen absolu

  • L’écart-type met les distances au carré, pénalisant davantage les longues distances que les courtes.
  • L’écart absolu moyen pénalise chaque distance de manière égale.
  • L’un n’est pas meilleur que l’autre, mais l’écart-type est plus courant que l’écart moyen absolu.
Introduction aux statistiques en Python

Quantiles

np.quantile(msleep['sleep_total'], 0.5)

10.1

$$

                        quantile de 0,5 = médiane

Quartiles :

np.quantile(msleep['sleep_total'], [0, 0.25, 0.5, 0.75, 1])

array([ 1.9 ,  7.85, 10.1 , 13.75, 19.9 ])
Introduction aux statistiques en Python

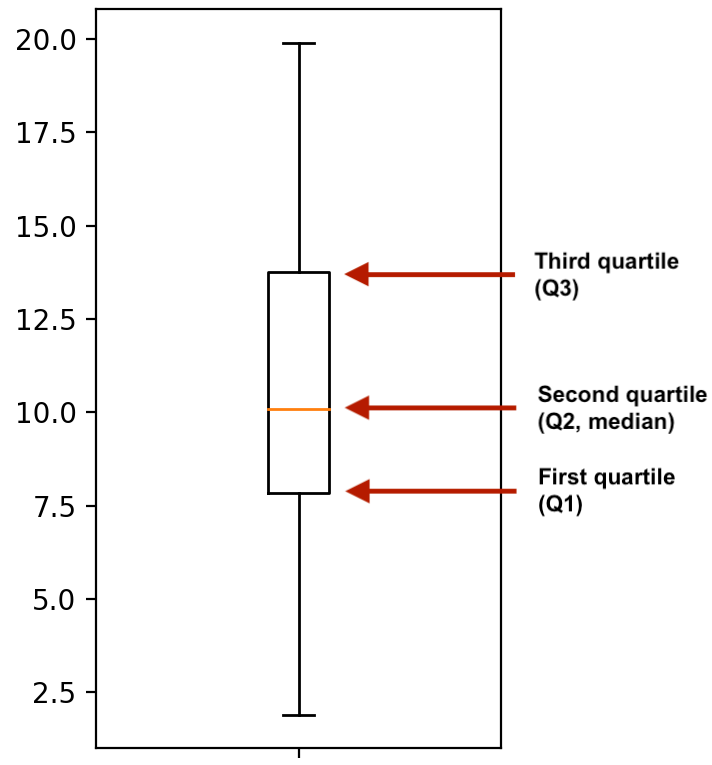
Les diagrammes en boîte utilisent les quartiles

import matplotlib.pyplot as plt
plt.boxplot(msleep['sleep_total'])
plt.show()

sleep_total boxplot.png

Introduction aux statistiques en Python

Quantiles avec np.linspace()

np.quantile(msleep['sleep_total'], [0, 0.2, 0.4, 0.6, 0.8, 1])

array([ 1.9 ,  6.24,  9.48, 11.14, 14.4 , 19.9 ])

 

np.linspace(valeur de départ, valeur d'arrêt, nombre d'intervalles)

np.quantile(msleep['sleep_total'], np.linspace(0, 1, 5))

array([ 1.9 ,  7.85, 10.1 , 13.75, 19.9 ])
Introduction aux statistiques en Python

Écart interquartile (IQR)

Hauteur de la boîte dans un diagramme en boîte

np.quantile(msleep['sleep_total'], 0.75) - np.quantile(msleep['sleep_total'], 0.25)

5.9

from scipy.stats import iqr
iqr(msleep['sleep_total'])

5.9
Introduction aux statistiques en Python

Valeurs aberrantes

Valeur aberrante : point de données très différent des autres

Comment savoir ce qu’est une différence substantielle ? Un point de données est une valeur aberrante si :

  • $\text{valeur} < \text{Q1} - 1,5\times\text{IQR}$ ou
  • $\text{valeur} > \text{Q3} + 1,5\times\text{IQR}$
Introduction aux statistiques en Python

Trouver les valeurs aberrantes

from scipy.stats import iqr
iqr = iqr(msleep['bodywt'])

lower_threshold = np.quantile(msleep['bodywt'], 0.25) - 1.5 * iqr
upper_threshold = np.quantile(msleep['bodywt'], 0.75) + 1.5 * iqr

msleep[(msleep['bodywt'] < lower_threshold) | (msleep['bodywt'] > upper_threshold)]

                    name   vore  sleep_total    bodywt
4                    Cow  herbi          4.0   600.000
20        Asian elephant  herbi          3.9  2547.000
22                 Horse  herbi          2.9   521.000
...
Introduction aux statistiques en Python

Tout en un

msleep['bodywt'].describe()

count      83.000000
mean      166.136349
std       786.839732
min         0.005000
25%         0.174000
50%         1.670000
75%        41.750000
max      6654.000000
Name: bodywt, dtype: float64
Introduction aux statistiques en Python

Passons à la pratique !

Introduction aux statistiques en Python

Preparing Video For Download...