Distributions discrètes
Introduction aux statistiques en Python

Maggie Matsui
Content Developer, DataCamp
Les dés sont jetés

Les dés sont jetés
Choix des vendeurs

Distribution des probabilités
Décrit la probabilité de chaque résultat possible dans un scénario
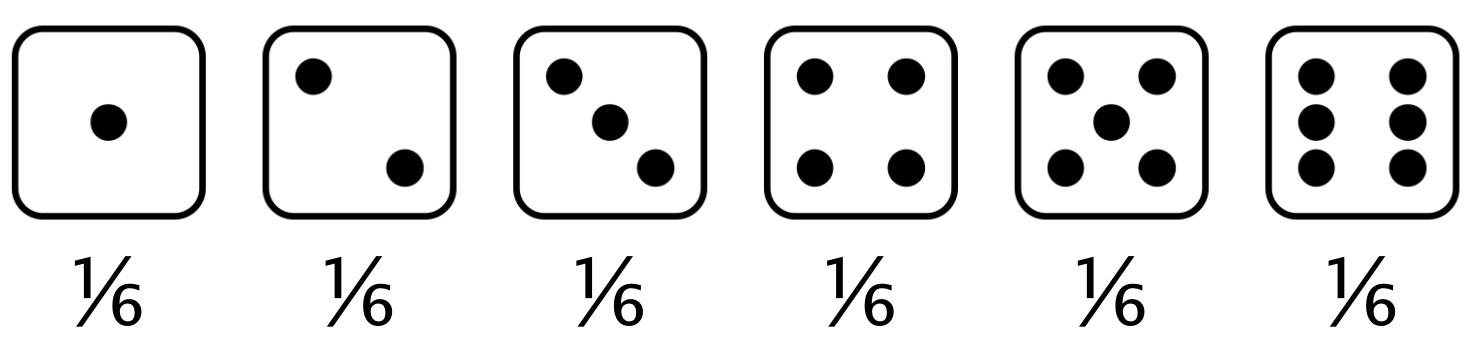
Valeur attendue : la moyenne d’une distribution des probabilités
Valeur attendue d’un lancer de dé équitable = $(1 \times \frac{1}{6}) + (2 \times \frac{1}{6}) +(3 \times \frac{1}{6}) +(4 \times \frac{1}{6}) +(5 \times \frac{1}{6}) +(6 \times \frac{1}{6}) = 3,5$.
Visualisation d’une distribution des probabilités
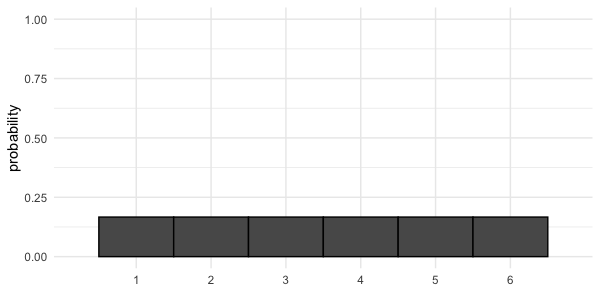
Probabilité = aire
$$P(\text{lancer de dé} \le 2) = ~?$$
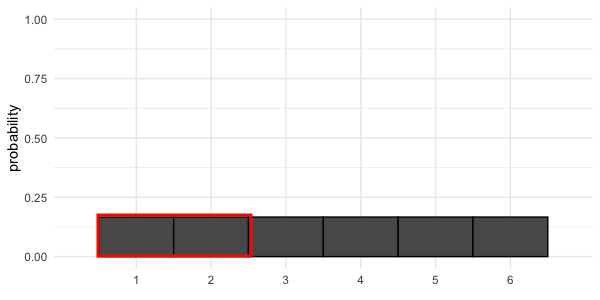
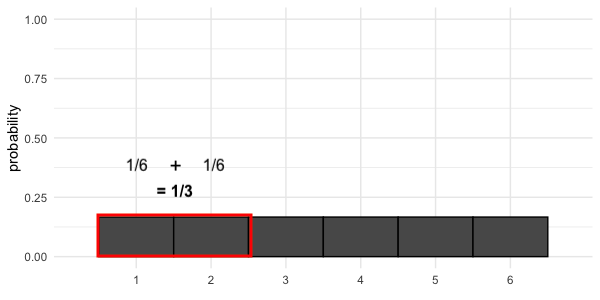
Probabilité = aire
$$P(\text{lancer de dé} \le 2) = 1/3$$
Dé irrégulier
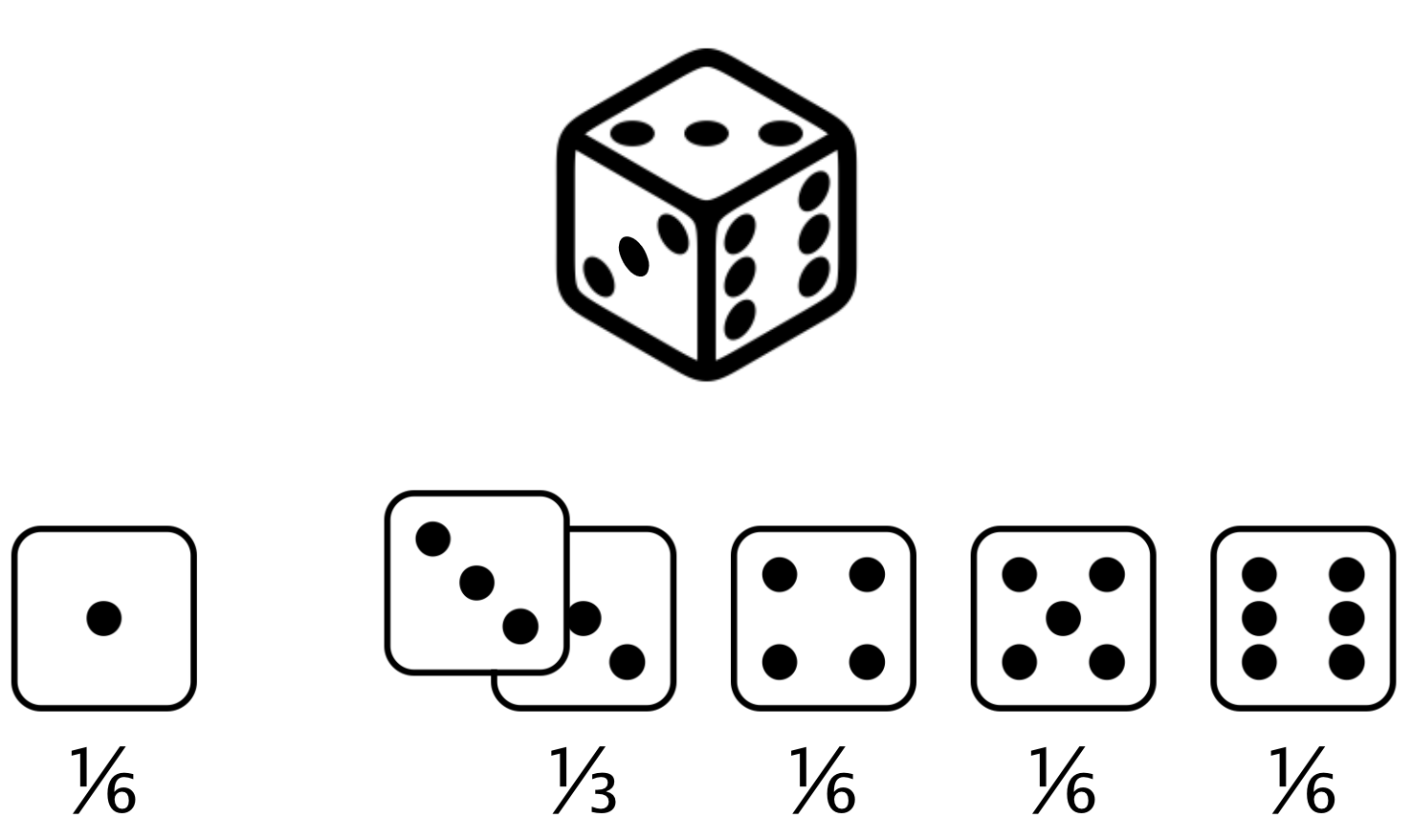
Valeur attendue d’un lancer de dé irrégulier = $(1 \times \frac{1}{6}) +(2 \times 0) +(3 \times \frac{1}{3}) +(4 \times \frac{1}{6}) +(5 \times \frac{1}{6}) +(6 \times \frac{1}{6}) = 3,67$
Visualiser des probabilités non uniformes
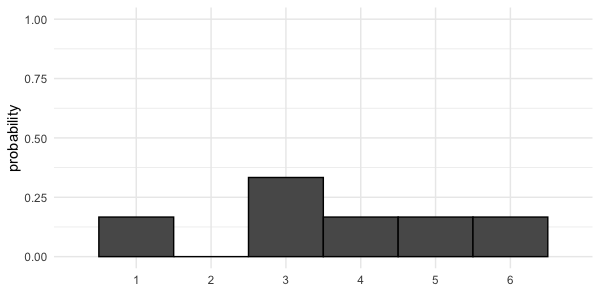
Addition d’aires
$$P(\text{lancer de dé irrégulier} \le 2) = ~?$$
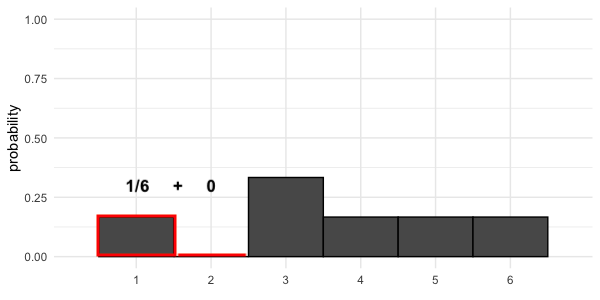
Addition d’aires
$$P(\text{lancer de dé irrégulier} \le 2) = 1/6$$

Distributions de probabilités discrètes
Décrit les probabilités pour des résultats discrets
Dé équitable

Distribution uniforme discrète
Dé irrégulier
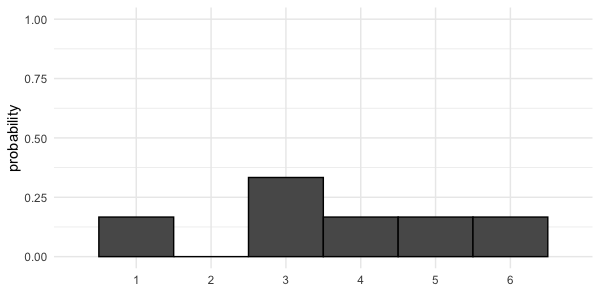
Échantillonnage à partir de distributions discrètes
print(die)
number prob
0 1 0.166667
1 2 0.166667
2 3 0.166667
3 4 0.166667
4 5 0.166667
5 6 0.166667
np.mean(die['number'])
3.5
rolls_10 = die.sample(10, replace = True)
rolls_10
number prob
0 1 0.166667
0 1 0.166667
4 5 0.166667
1 2 0.166667
0 1 0.166667
0 1 0.166667
5 6 0.166667
5 6 0.166667
...
Visualisation d’un échantillon
rolls_10['number'].hist(bins=np.linspace(1,7,7))
plt.show()
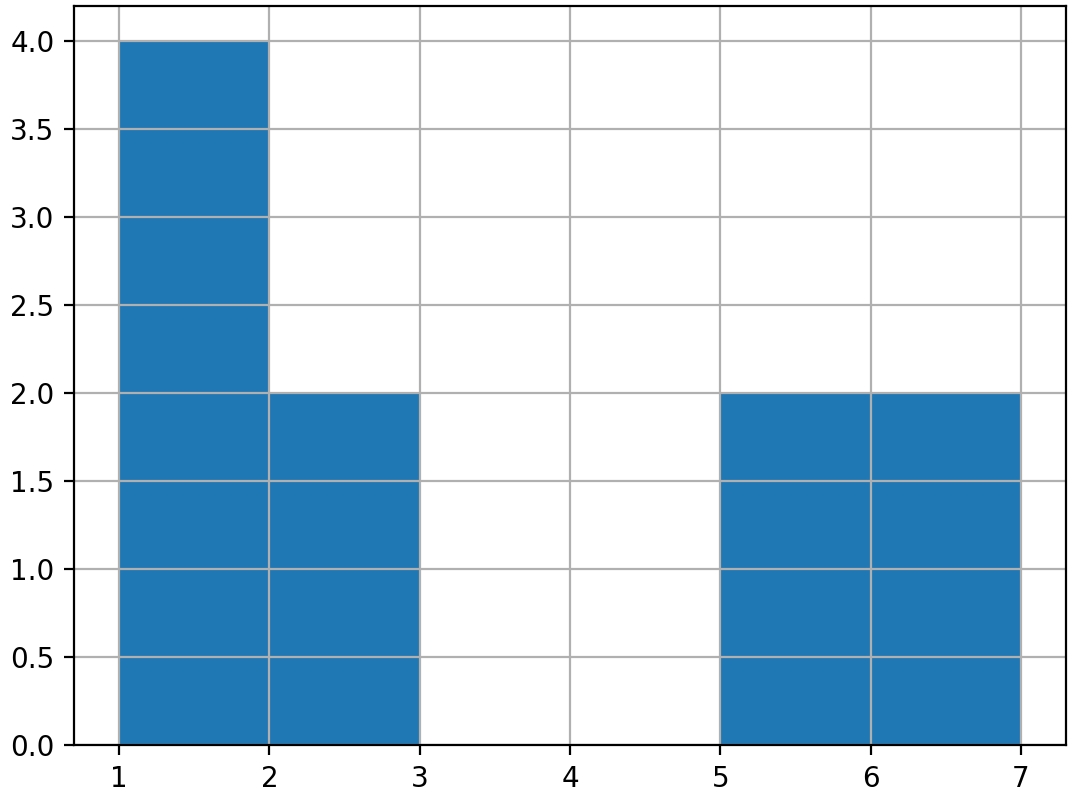
Distribution de l’échantillon et distribution théorique
Échantillon de 10 lancers

np.mean(rolls_10['number']) = 3.0
Distribution théorique
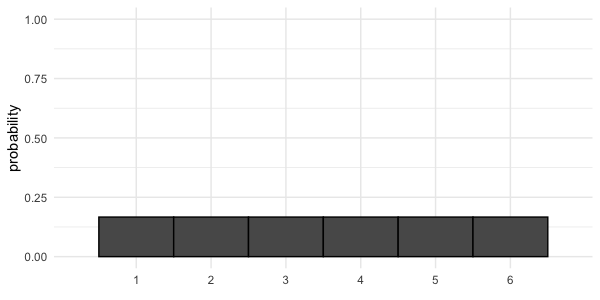
mean(die['number']) = 3.5
Un échantillon plus important
Échantillon de 100 lancers
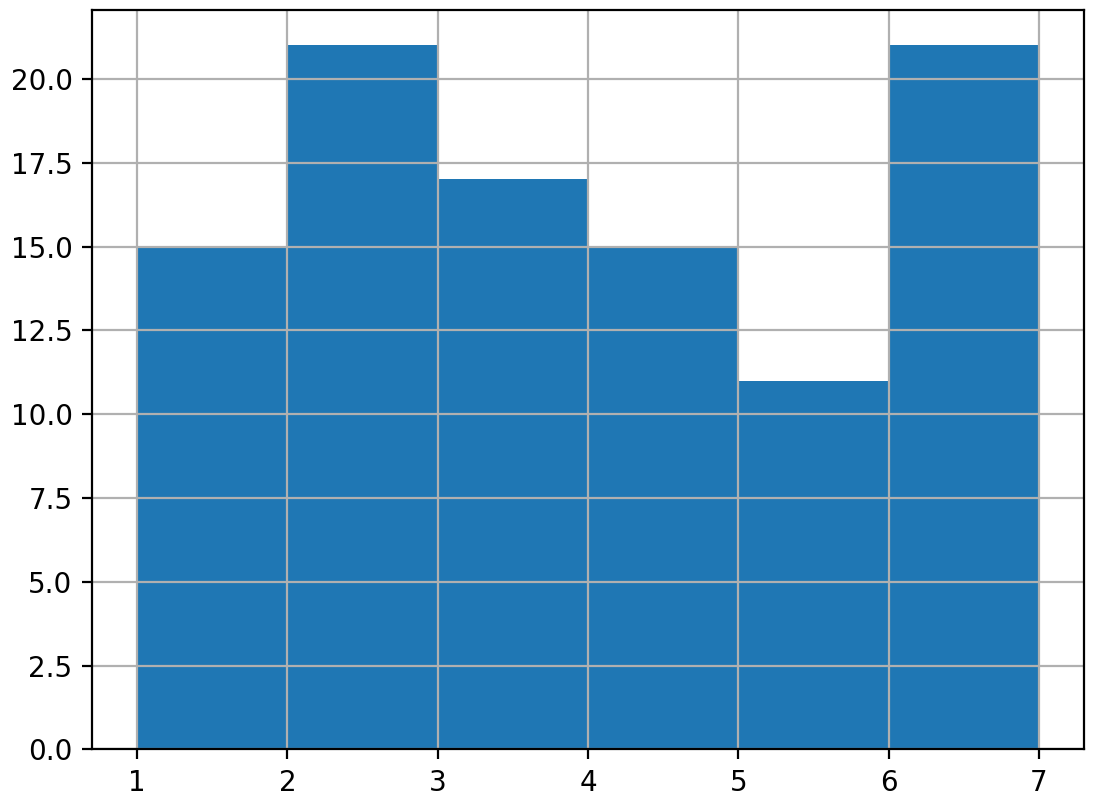
np.mean(rolls_100['number']) = 3.4
Distribution théorique

mean(die['number']) = 3.5
Un échantillon encore plus important
Échantillon de 1000 lancers
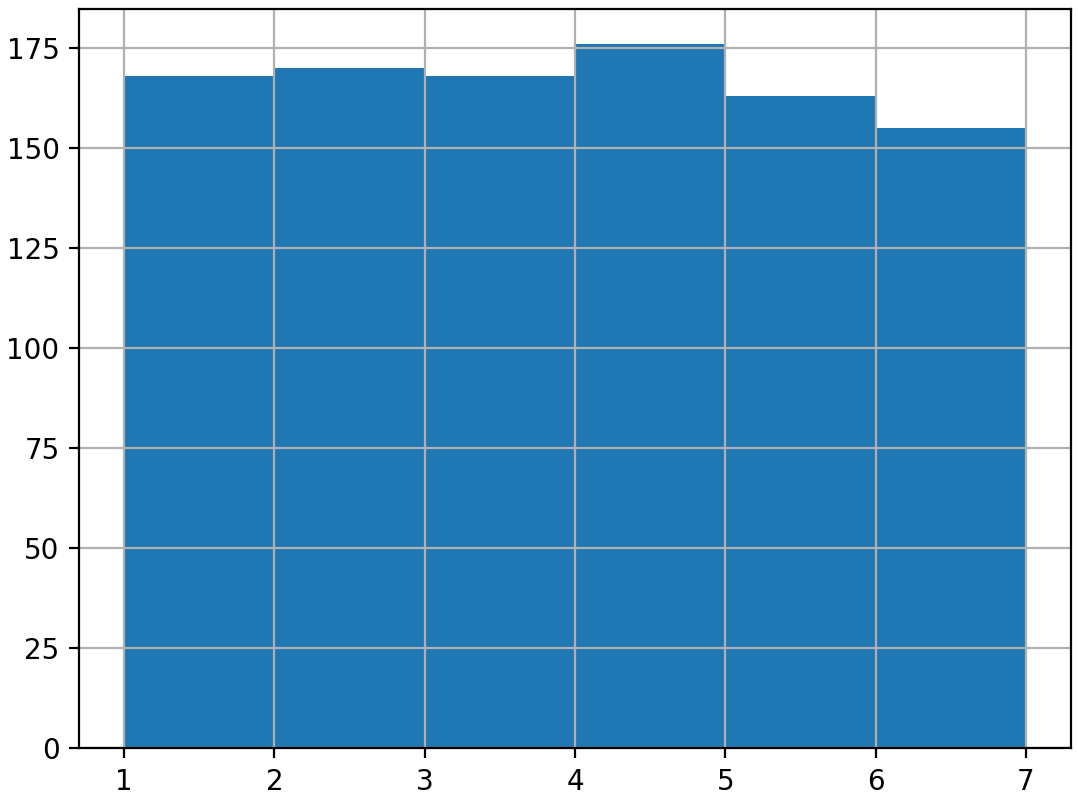
np.mean(rolls_1000['number']) = 3.48
Distribution théorique

mean(die['number']) = 3.5
La loi des grands nombres
Au fur et à mesure que la taille de votre échantillon augmente, la moyenne de l’échantillon se rapproche de la valeur attendue.
| Taille de l’échantillon | Moyenne |
|---|---|
| 10 | 3,00 |
| 100 | 3,40 |
| 1000 | 3,48 |
Passons à la pratique !
Introduction aux statistiques en Python

