Random Walk

Time Series Analysis in Python

Rob Reider

Adjunct Professor, NYU-Courant Consultant, Quantopian

What is a Random Walk?

Today's Price = Yesterday's Price + Noise

$\large \quad \quad \ P_t \quad \ \ = \quad P_{t-1} \quad \quad \ + \ \ \epsilon_t$

Plot of simulated data

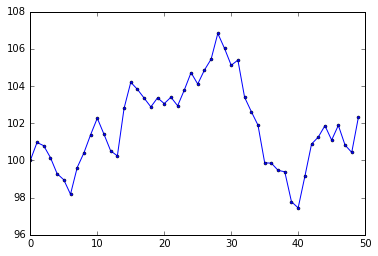
What is a Random Walk?

Today's Price = Yesterday's Price + Noise

$\large \quad \quad \ P_t \quad \ \ = \quad P_{t-1} \quad \quad \ + \ \ \epsilon_t$

Change in price is white noise

$\large \quad \quad P_t - P_{t-1} \quad \ \ = \quad \ \ \epsilon_t$

Can't forecast a random walk
Best forecast for tomorrow's price is today's price

What is a Random Walk?

Today's Price = Yesterday's Price + Noise

$\large \quad \quad \ P_t \quad \ \ = \quad P_{t-1} \quad \quad \ + \ \ \epsilon_t$

Random walk with drift:

$\large \quad \quad \ P_t \quad \ \ = \ \mu \ + \ P_{t-1} \ \ + \quad \epsilon_t$

Change in price is white noise with non-zero mean:

$\large \quad \quad P_t - P_{t-1} \ \ = \ \mu \ \ + \ \ \epsilon_t$

Statistical Test for Random Walk

Random walk with drift

$\large \quad \quad P_t \quad \ \ = \ \mu \ \ + \ \ P_{t-1} \quad \ + \ \ \epsilon_t$

Regression test for random walk

$\large \quad \quad P_t \quad \ \ = \ \alpha \ \ + \ \ \beta \ P_{t-1} \ \ + \ \ \epsilon_t$

Test:

$\quad \quad \large H_0: \beta=1$ (random walk)

$\quad \quad \large H_1: \beta<1$ (not random walk)

Statistical Test for Random Walk

Regression test for random walk

$\large \quad \quad \quad \quad P_t \quad \ \ = \ \alpha \ \ + \ \ \beta \ P_{t-1} \quad \ + \ \ \epsilon_t$

Equivalent to

$\large \quad \quad P_t - P_{t-1} \ \ = \ \alpha \ \ + \ \ \beta \ P_{t-1} \ \ + \ \ \epsilon_t$

Test:

$\quad \quad \large H_0: \beta=0$ (random walk)

$\quad \quad \large H_1: \beta<0$ (not random walk)

Statistical Test for Random Walk

Regression test for random walk

$\large \quad \quad P_t - P_{t-1} \ \ = \ \alpha \ \ + \ \ \beta \ P_{t-1} \ \ + \ \ \epsilon_t$

Test:

$\large \ \ \ \ H_0: \beta=0$ (random walk)

$\large \ \ \ \ H_1: \beta<0$ (not random walk)

This test is called the Dickey-Fuller test
If you add more lagged changes on the right hand side, it's the Augmented Dickey-Fuller test

ADF Test in Python

Import module from statsmodels

from statsmodels.tsa.stattools import adfuller

Run Augmented Dickey-Test
```
adfuller(x)
```

Example: Is the S&P500 a Random Walk?

# Run Augmented Dickey-Fuller Test on SPX data
results = adfuller(df['SPX'])

# Print p-value
print(results[1])

0.782253808587

# Print full results
print(results)

(-0.91720490331127869,
 0.78225380858668414,
 0,
 1257,
 {'1%': -3.4355629707955395,
  '10%': -2.567995644141416,
  '5%': -2.8638420633876671},
 10161.888789598503)

Let's practice!

Time Series Analysis in Python