Die Relevanz logistischer Regression

Einführung in Regression mit R

Richie Cotton

Data Evangelist at DataCamp

Kundenabwanderung einer Bank

has_churned	time_since_first_purchase	time_since_last_purchase
0	0,3993247	-0,5158691
1	-0,4297957	0,6780654
0	3,7383122	0,4082544
0	0,6032289	-0,6990435
...	...	...
Antwort	Dauer der Geschäftsbeziehung	Aktualität der Aktivität

¹ https://www.rdocumentation.org/packages/bayesQR/topics/Churn

Abwanderung vs. Aktualität: ein lineares Modell

mdl_churn_vs_recency_lm <- lm(has_churned ~ time_since_last_purchase, data = churn)

Call:
lm(formula = has_churned ~ time_since_last_purchase, data = churn)

Coefficients:
             (Intercept)  time_since_last_purchase  
                 0.49078                   0.06378

coeffs <- coefficients(mdl_churn_vs_recency_lm)
intercept <- coeffs[1]
slope <- coeffs[2]

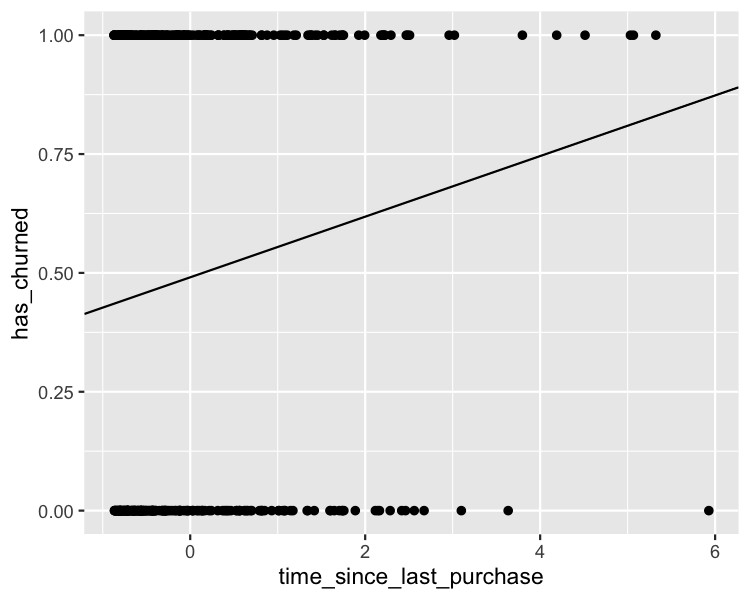
Das lineare Modell visualisieren

ggplot(
  churn, 
  aes(time_since_last_purchase, has_churned)
) +
  geom_point() +
  geom_abline(intercept = intercept, slope = slope)

Prognosen sind Wahrscheinlichkeiten für Abwanderungen, keine absolute Zahlen zu Abwanderungen.

Ein Streudiagramm, das zeigt, ob der Kunde abgewandert ist oder nicht, im Vergleich zur Zeit seit dem letzten Kauf. Alle Punkte liegen auf der Geraden y = 0 oder y = 1. Eine lineare Trendlinie zeigt, dass die Wahrscheinlichkeit einer Abwanderung mit zunehmender Zeit seit dem letzten Kauf steigt.

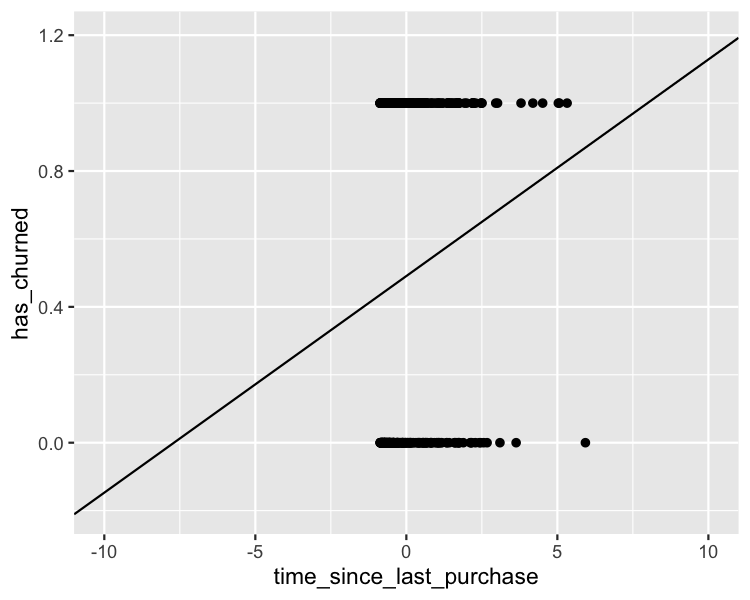
Der Blick auf große Ganze

ggplot(
  churn, 
  aes(days_since_last_purchase, has_churned)
) +
  geom_point() +
  geom_abline(intercept = intercept, slope = slope) +
  xlim(-10, 10) +
  ylim(-0.2, 1.2)

Das Streudiagramm zeigt, ob der Kunde abgewandert ist oder nicht, im Vergleich zur Zeit seit dem letzten Kauf. Die Achsen sind im Vergleich zum letzten Mal verkleinert, was zeigt, dass die Trendlinie unterhalb von y gleich 0 und oberhalb von y gleich 1 verläuft, was eigentlich nicht möglich sein sollte.

Was ist logistische Regression?

Eine andere Art verallgemeinertes lineares Modell.
Wird benutzt, wenn die Antwortvariable logistisch ist.
Die Antworten folgen einer logistischen (S-förmigen) Kurve.

Lineare Regression mit glm()

glm(has_churned ~ time_since_last_purchase, data = churn, family = gaussian)

Call:  glm(formula = has_churned ~ time_since_last_purchase, family = gaussian, 
    data = churn)

Coefficients:
             (Intercept)  time_since_last_purchase  
                 0.49078                   0.06378  

Degrees of Freedom: 399 Total (i.e. Null);  398 Residual
Null Deviance:        100 
Residual Deviance: 98.02     AIC: 578.7

Logistische Regression: glm() mit binomialer Verteilung

mdl_recency_glm <- glm(has_churned ~ time_since_last_purchase, data = churn, family = binomial)

Call:  glm(formula = has_churned ~ time_since_last_purchase, family = binomial, 
    data = churn)

Coefficients:
             (Intercept)  time_since_last_purchase  
                -0.03502                   0.26921  

Degrees of Freedom: 399 Total (i.e. Null);  398 Residual
Null Deviance:        554.5 
Residual Deviance: 546.4     AIC: 550.4

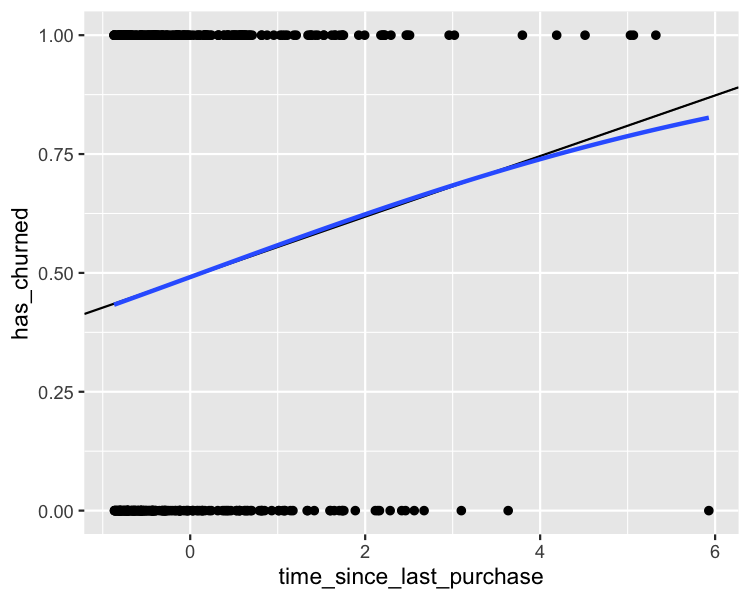
Das logistische Modell visualisieren

ggplot(
  churn, 
  aes(time_since_last_purchase, has_churned)
) +
  geom_point() +
  geom_abline(
    intercept = intercept, slope = slope
  ) +
  geom_smooth(
    method = "glm", 
    se = FALSE, 
    method.args = list(family = binomial)
  )

Ein Streudiagramm, das zeigt, ob der Kunde abgewandert ist oder nicht, im Vergleich zur Zeit seit dem letzten Kauf. Es werden lineare und logistische Trendlinien angezeigt, die beide zeigen, dass die Wahrscheinlichkeit einer Abwanderung mit zunehmender Zeit seit dem letzten Kauf steigt. Die beiden Trendlinien laufen ziemlich nah beieinander, außer seit dem letzten Kauf.

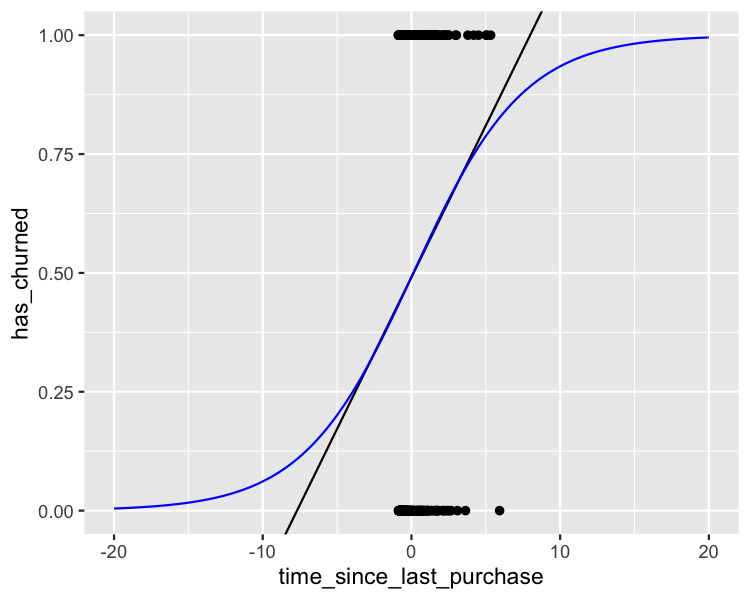
Der Blick auf große Ganze

Das Streudiagramm zeigt, ob der Kunde abgewandert ist oder nicht, im Vergleich zur Zeit seit dem letzten Kauf, mit beiden Trendlinien. Die Achsen sind im Vergleich zum letzten Mal verkleinert, was zeigt, dass die logistische Trendlinie nie außerhalb des Bereichs von null bis eins liegt.

Lass uns üben!

Einführung in Regression mit R