Ausreißer, Hebelwerte und Einfluss

Einführung in Regression mit R

Richie Cotton

Data Evangelist at DataCamp

Rotaugendatensatz

roach <- fish %>%
  filter(species == "Roach")

Art	length_cm	mass_g
Rotauge	12,9	40
Rotauge	16,5	69
Rotauge	17,5	78
Rotauge	18,2	87
Rotauge	18,6	120
...	...	...

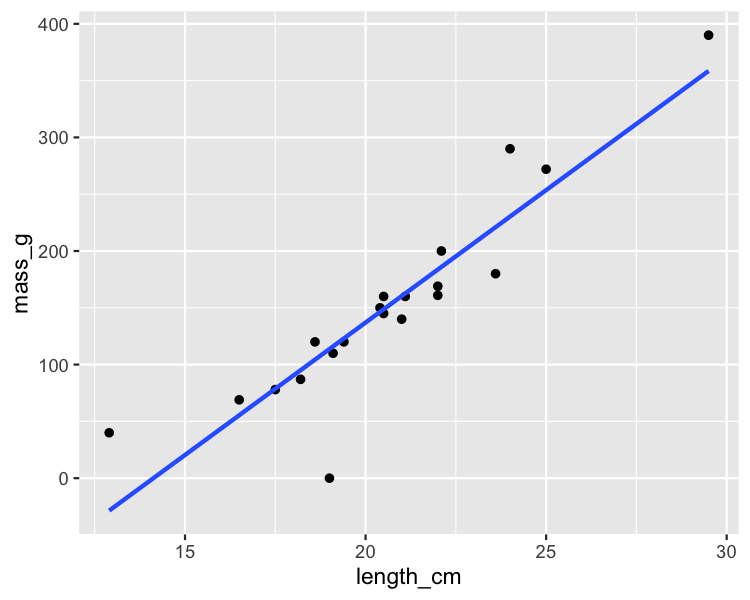
Welche Punkte sind Ausreißer?

ggplot(roach, aes(length_cm, mass_g)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE)

Ein Streudiagramm der Masse von Rotaugen im Vergleich zu ihrer Länge, mit einer Trendlinie. Die meisten Punkte folgen ziemlich genau der Trendlinie.

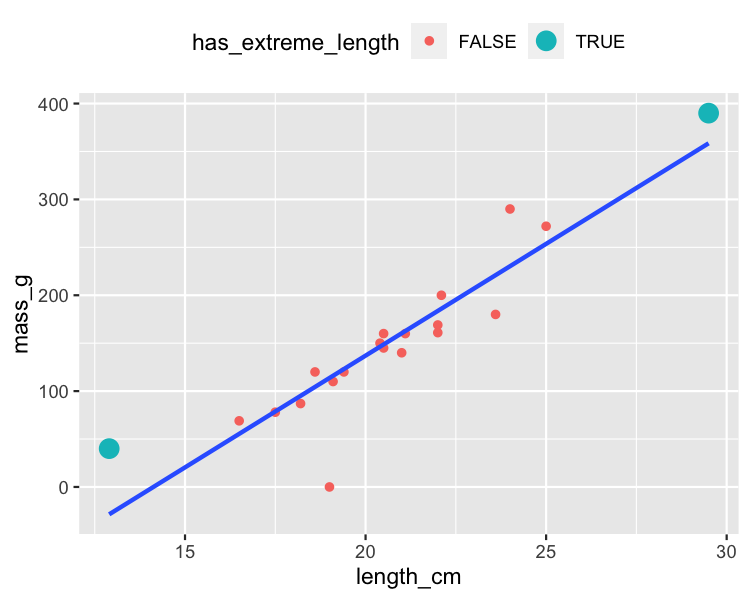
Extreme erklärende Werte

roach %>% 
  mutate(
    has_extreme_length = length_cm < 15 | length_cm > 26
  ) %>% 
  ggplot(aes(length_cm, mass_g)) +
  geom_point(aes(color = has_extreme_length)) +
  geom_smooth(method = "lm", se = FALSE)

Ein Streudiagramm der Masse von Rotaugen im Vergleich zu ihrer Länge, mit einer Trendlinie. Die meisten Punkte sind rot, aber ein ganz kurzer und ein ganz langer Kakerlak haben Punkte in Cyan.

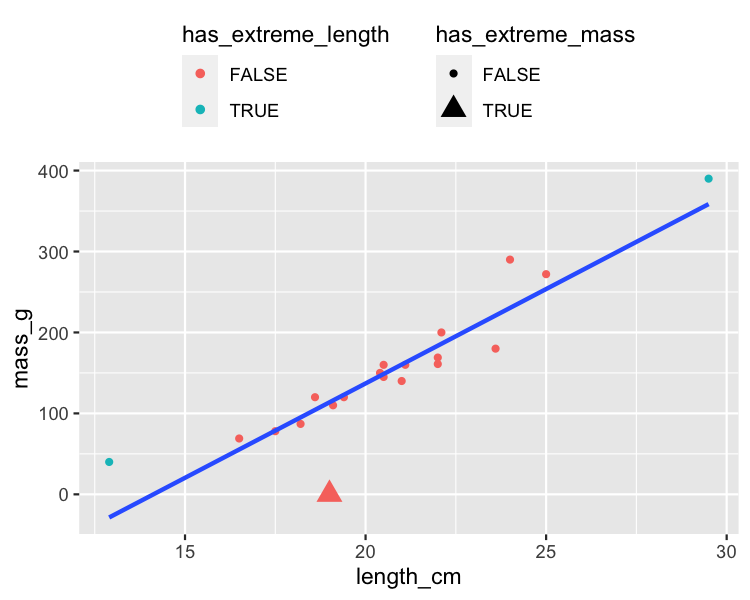
Werte, die von der Regressionsgeraden abweichen

roach %>% 
  mutate(
    has_extreme_length = length_cm < 15 | length_cm > 26,
    has_extreme_mass = mass_g < 1
  ) %>% 
  ggplot(aes(length_cm, mass_g)) +
  geom_point(
    aes(
      color = has_extreme_length, 
      shape = has_extreme_mass
    )
  ) +
  geom_smooth(method = "lm", se = FALSE)

Ein Streudiagramm der Masse von Rotaugen im Vergleich zu ihrer Länge, mit einer Trendlinie. Die meisten Punkte sind rot, aber ein ganz kurzer und ein ganz langer Kakerlak haben Punkte in Cyan. Die meisten Punkte sind Kreise, aber ein Punkt, der einen Fisch mit einer scheinbaren Masse von Null darstellt, ist ein Dreieck.

Hebelwerte

Hebelwert ein Maß dafür, wie extrem die Werte der erklärenden Variablen sind.

mdl_roach <- lm(mass_g ~ length_cm, data = roach)

hatvalues(mdl_roach)

     1      2      3      4      5      6      7 
0.3137 0.1255 0.0935 0.0763 0.0684 0.0619 0.0605 
     8      9     10     11     12     13     14 
0.0568 0.0503 0.0501 0.0501 0.0506 0.0509 0.0581 
    15     16     17     18     19     20 
0.0581 0.0593 0.0884 0.0995 0.1334 0.3947

Die Spalte „.hat“

library(broom)
augment(mdl_roach)

# A tibble: 20 × 8
   mass_g length_cm .fitted   .resid   .hat .sigma   .cooksd .std.resid
    <dbl>     <dbl>   <dbl>    <dbl>  <dbl>  <dbl>     <dbl>      <dbl>
 1     40      12.9   -28.6   68.6   0.314    33.8 1.07          2.17  
 2     69      16.5    55.4   13.6   0.126    39.1 0.0104        0.381 
 3     78      17.5    78.7   -0.711 0.0935   39.3 0.0000197    -0.0196
 4     87      18.2    95.0   -8.03  0.0763   39.2 0.00198      -0.219 
 5    120      18.6   104.    15.6   0.0684   39.1 0.00661       0.424 
...

Schaben mit extremen Hebelwerten

mdl_roach %>%
  augment() %>%
  select(mass_g, length_cm, leverage = .hat) %>%
  arrange(desc(leverage)) %>% 
  head()

# A tibble: 6 x 3
  mass_g length_cm leverage
   <dbl>     <dbl>    <dbl>
1    390      29.5   0.395  # really long roach
2     40      12.9   0.314  # really short roach
3    272      25     0.133 
4     69      16.5   0.126 
5    290      24     0.0995
6     78      17.5   0.0935

Einfluss

Der Einfluss misst, wie stark sich das Modell ändern würde, wenn man eine bestimmte Beobachtung bei der Modellierung aus dem Datensatz weglassen würde.

Jemand, der einen Schraubenschlüssel dreht

Cook-Distanz

Die Cook-Distanz ist das gängigste Maß für den Einfluss.

cooks.distance(mdl_roach)

       1        2        3        4        5        6 
1.07e+00 1.04e-02 1.97e-05 1.98e-03 6.61e-03 3.12e-01 
       7        8        9       10       11       12 
8.53e-04 1.99e-04 2.57e-04 2.56e-04 2.45e-03 7.95e-03 
      13       14       15       16       17       18 
1.37e-04 4.82e-03 1.15e-02 4.52e-03 6.12e-02 1.50e-01 
      19       20 
2.06e-02 3.66e-01

Die Spalte „.cooksd“

library(broom)
augment(mdl_roach)

# A tibble: 20 x 9
   mass_g length_cm .fitted .se.fit   .resid   .hat .sigma   .cooksd .std.resid
    <dbl>     <dbl>   <dbl>   <dbl>    <dbl>  <dbl>  <dbl>     <dbl>      <dbl>
 1     40      12.9   -28.6   21.4    68.6   0.314    33.8 1.07          2.17  
 2     69      16.5    55.4   13.5    13.6   0.126    39.1 0.0104        0.381 
 3     78      17.5    78.7   11.7    -0.711 0.0935   39.3 0.0000197    -0.0196
 4     87      18.2    95.0   10.5    -8.03  0.0763   39.2 0.00198      -0.219 
 5    120      18.6   104.     9.98   15.6   0.0684   39.1 0.00661       0.424 
...

Die einflussreichsten Rotaugen

mdl_roach %>%
  augment() %>%
  select(mass_g, length_cm, cooks_dist = .cooksd) %>%
  arrange(desc(cooks_dist)) %>% 
  head()

# A tibble: 6 x 3
  mass_g length_cm cooks_dist
   <dbl>     <dbl>      <dbl>
1     40      12.9     1.07   # really short roach
2    390      29.5     0.366  # really long roach
3      0      19       0.312  # zero mass roach
4    290      24       0.150 
5    180      23.6     0.0612
6    272      25       0.0206

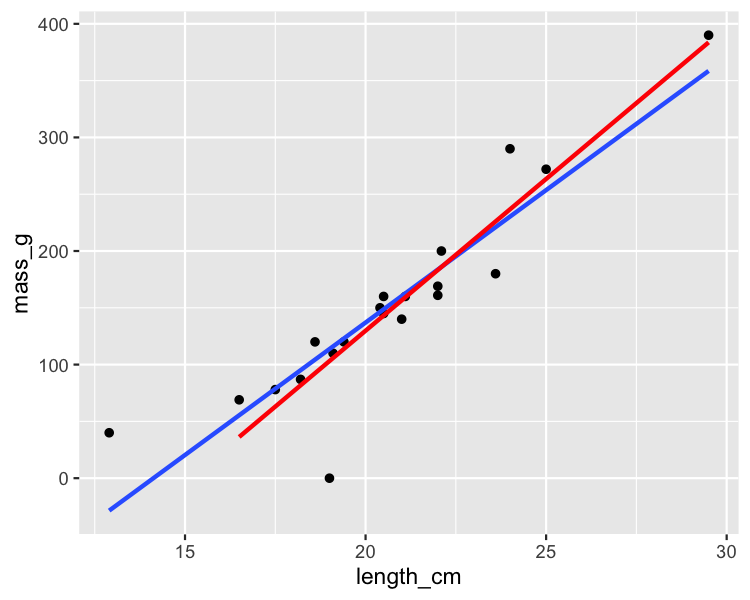
Das einflussreichste Rotauge loswerden

roach_not_short <- roach %>% 
  filter(length != 12.9)

ggplot(roach, aes(length_cm, mass_g)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE) +
  geom_smooth(
    method = "lm", se = FALSE, 
    data = roach_not_short, color = "red"
  )

Ein Streudiagramm der Masse von Rotaugen im Vergleich zu ihrer Länge, mit zwei Trendlinien. Eine Trendlinie nutzt alle Daten, die andere lässt das kürzeste Rotauge weg. Die zweite Trendlinie hat einen deutlich steileren Anstieg.

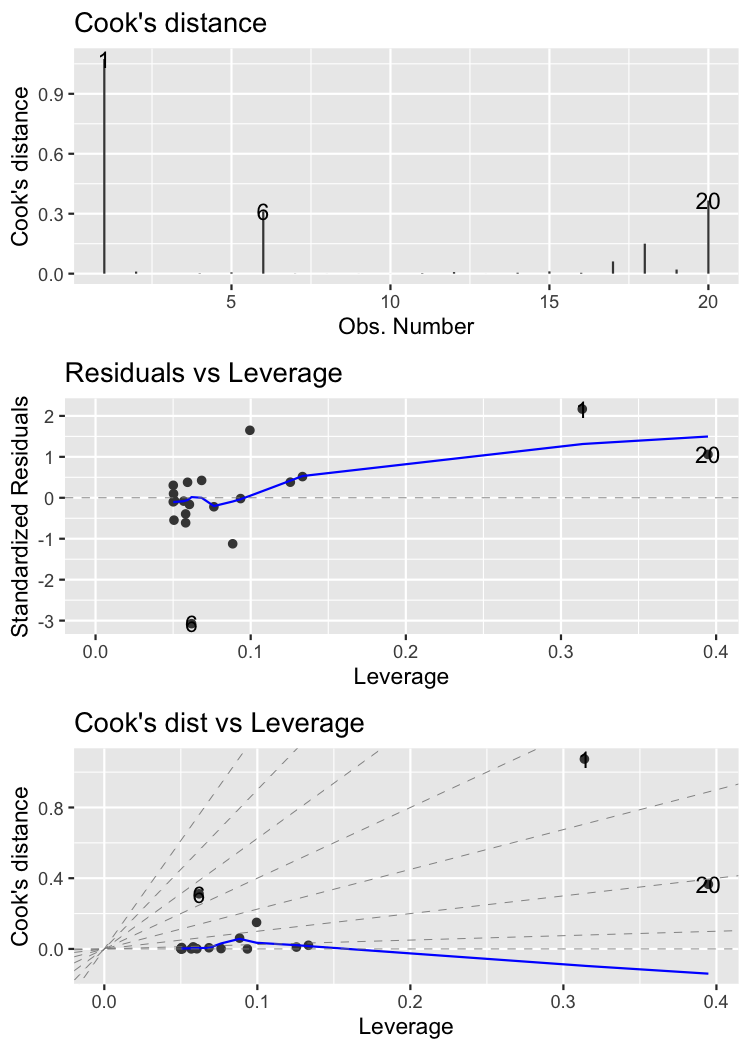
autoplot()

autoplot(
  mdl_roach, 
  which = 4:6, 
  nrow = 3,
  ncol = 1
)

Die drei Diagnoseplots des Rotaugenmodells, angeordnet in drei Feldern.

Lass uns üben!

Einführung in Regression mit R