Variablen umwandeln

Einführung in Regression mit R

Richie Cotton

Data Evangelist at DataCamp

Barsch-Datensatz

library(dplyr)

perch <- fish %>%
  filter(species == "Perch")

Art	mass_g	length_cm
Barsch	5,9	7,5
Barsch	32,0	12,5
Barsch	40,0	13,8
Barsch	51,5	15,0
Barsch	70,0	15,7
...	...	...

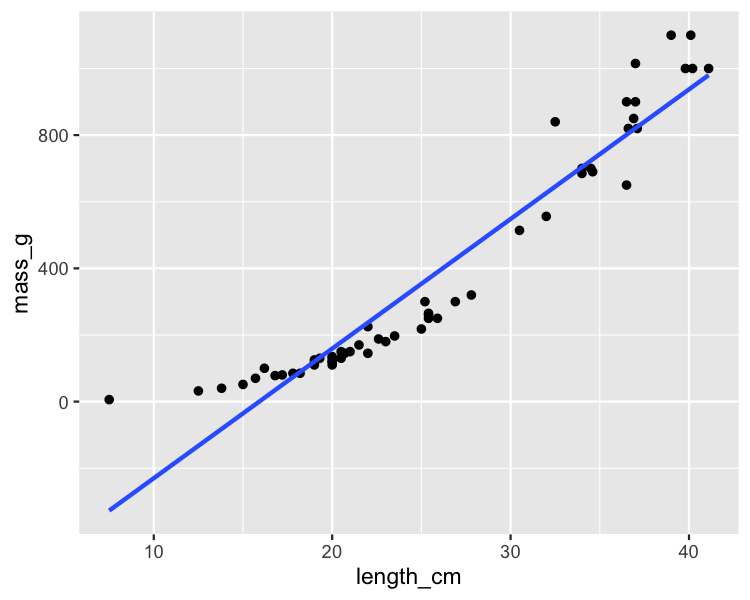
Keine lineare Beziehung

ggplot(perch, aes(length_cm, mass_g)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE)

Ein Streudiagramm der Masse von Barschen im Vergleich zu ihrer Länge, mit einer Trendlinie. Die Stangen werden mit zunehmender Länge schneller als linear schwerer, was zu einer Aufwärtskurve führt.

Brassen gegen Barsche

Ein paar Brassen schwimmen rum. Brassen sind ziemlich flach.

Ein paar Barsche schwimmen. Barsch sind ziemlich rund.

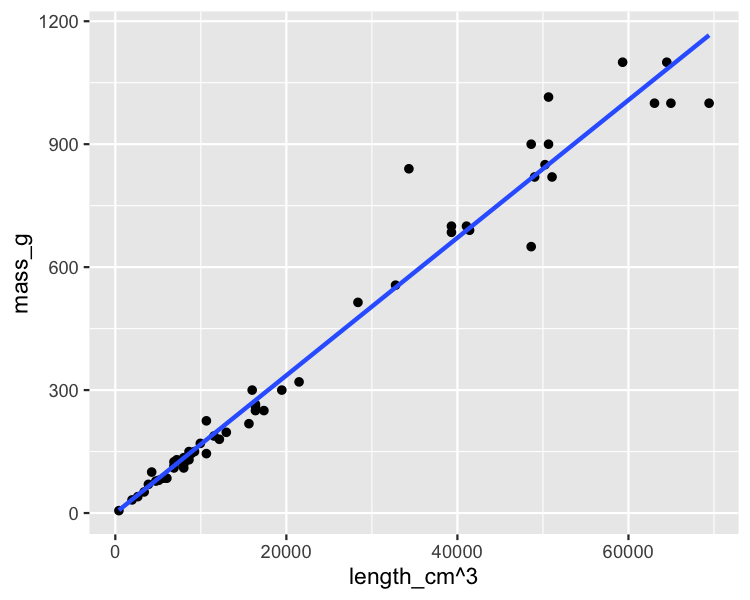
Darstellung von: Masse und Länge hoch drei

ggplot(perch, aes(length_cm ^ 3, mass_g)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE)

Ein Streudiagramm der Masse von Barschen im Vergleich zu ihrer Länge hoch drei, mit einer Trendlinie. Nach dieser Transformation liegen fast alle Punkte nah an der Trendlinie.

Modellierung von Masse und Länge hoch drei

mdl_perch <- lm(mass_g ~ I(length_cm ^ 3), data = perch)

Call:
lm(formula = mass_g ~ I(length_cm^3), data = perch)

Coefficients:
   (Intercept)  I(length_cm^3)  
       -0.1175          0.0168

Vorhersage von Masse im Verhältnis zur Länge hoch drei

explanatory_data <- tibble(
  length_cm = seq(10, 40, 5)
)

prediction_data <- explanatory_data %>%
  mutate(
    mass_g = predict(mdl_perch, explanatory_data)
  )

# A tibble: 7 x 2
  length_cm mass_g
      <dbl>  <dbl>
1        10   16.7
2        15   56.6
3        20  134. 
4        25  262. 
5        30  453. 
6        35  720. 
7        40 1075.

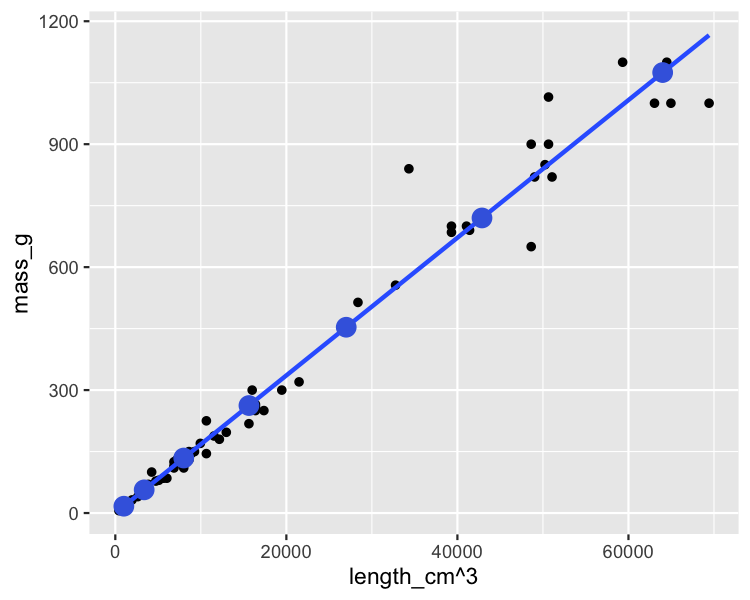
Darstellung von: Masse und Länge hoch drei

ggplot(perch, aes(length_cm ^ 3, mass_g)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE) +
  geom_point(data = prediction_data, color = "blue")

Das Streudiagramm der Barschmassen im Vergleich zu ihrer Länge hoch drei, mit einer Trendlinie und mit Punkten versehen, die mit der Funktion predict() berechnet wurden. Die Punkte folgen genau der Trendlinie.

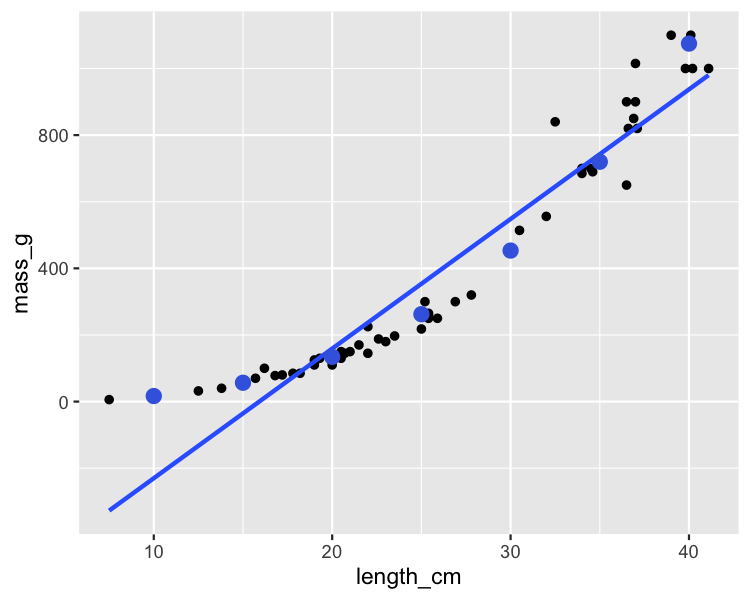
ggplot(perch, aes(length_cm, mass_g)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE) +
  geom_point(data = prediction_data, color = "blue")

Das Streudiagramm der Masse von Barschen im Vergleich zu ihrer Länge, mit einer Trendlinie und mit Punkten, die mit der Funktion predict() berechnet wurden. Die Punkte folgen nicht der Trendlinie, aber sie folgen der Kurve der Datenpunkte.

Facebook-Werbedatensatz

Wie Werbung funktioniert

Bezahle Facebook dafür, deine Werbung zu zeigen.
Menschen sehen die Anzeigen („impressions“).
Manche Menschen, die sie sehen, klicken drauf.

936 Zeilen
Jede Zeile steht für eine Anzeige.

spent_usd	n_impressions	n_clicks
1,43	7.350	1
1,82	17.861	2
1,25	4.259	1
1,29	4.133	1
4,77	15.615	3
...	...	...

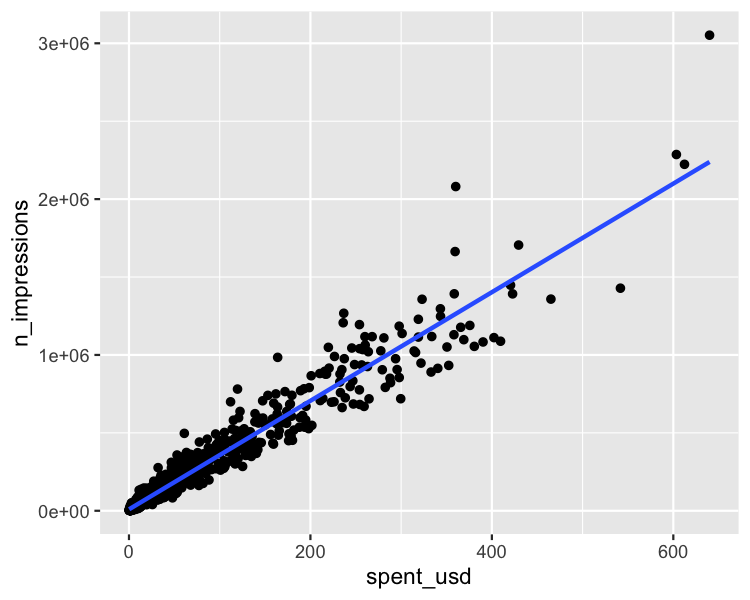
Die Grafik ist ziemlich gedrängt.

ggplot(
  ad_conversion, 
  aes(spent_usd, n_impressions)
) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE)

Ein Streudiagramm, das die Anzahl der Impressionen gegen die Werbeausgaben zeigt, mit einer Trendlinie. Die meisten Datenpunkte sind unten links im Diagramm zusammengepfercht.

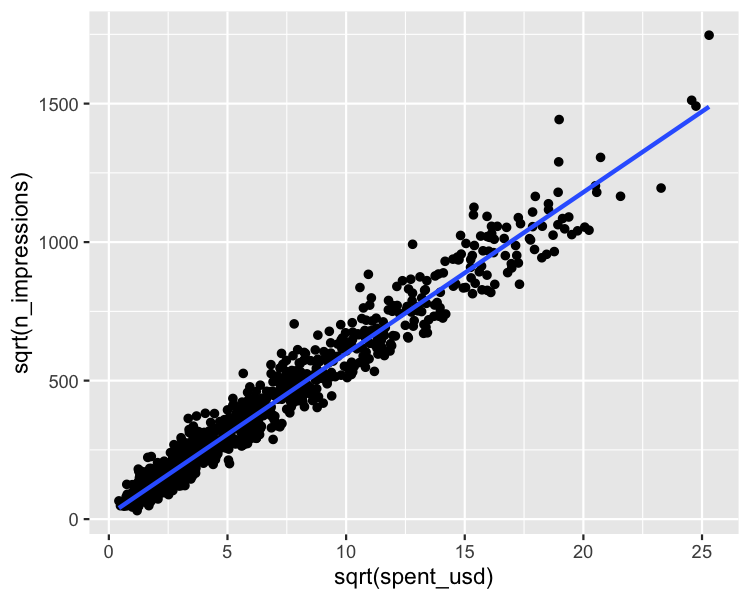
Quadratwurzel vs. Quadratwurzel

ggplot(
  ad_conversion, 
  aes(sqrt(spent_usd), sqrt(n_impressions))
) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE)

Ein Streudiagramm der Quadratwurzel der Anzahl der Impressionen gegen die Quadratwurzel der Werbeausgaben, mit einer Trendlinie. Jetzt sind die Punkte gleichmäßiger über das Grundstück verteilt.

Modellierung und Vorhersage

mdl_ad <- lm(
  sqrt(n_impressions) ~ sqrt(spent_usd), 
  data = ad_conversion
)

explanatory_data <- tibble(
  spent_usd = seq(0, 600, 100)
)

prediction_data <- explanatory_data %>% 
  mutate(
    sqrt_n_impressions = predict(
      mdl_ad, explanatory_data
    ),
    n_impressions = sqrt_n_impressions ^ 2
  )

# A tibble: 7 x 3
  spent_usd sqrt_n_impressions n_impressions
      <dbl>              <dbl>         <dbl>
1         0               15.3          235.
2       100              598.        357289.
3       200              839.        703890.
4       300             1024.       1048771.
5       400             1180.       1392762.
6       500             1318.       1736184.
7       600             1442.       2079202.

Lass uns üben!

Einführung in Regression mit R