Quantifizierung einer logistischen Regressionsanpassung
Einführung in Regression mit R

Richie Cotton
Data Evangelist at DataCamp
Die vier Ergebnisse
| Tatsächlich falsch | Tatsächlich wahr | |
|---|---|---|
| Falsch vorhergesagt | Korrekt | Falsch negativ |
| Richtig vorhergesagt | Falsch positiv | Korrekt |
Konfusionsmatrix: Anzahl der Ergebnisse
mdl_recency <- glm(has_churned ~ time_since_last_purchase, data = churn, family = "binomial")
actual_response <- churn$has_churned
predicted_response <- round(fitted(mdl_recency))
outcomes <- table(predicted_response, actual_response)
actual_response
predicted_response 0 1
0 141 111
1 59 89
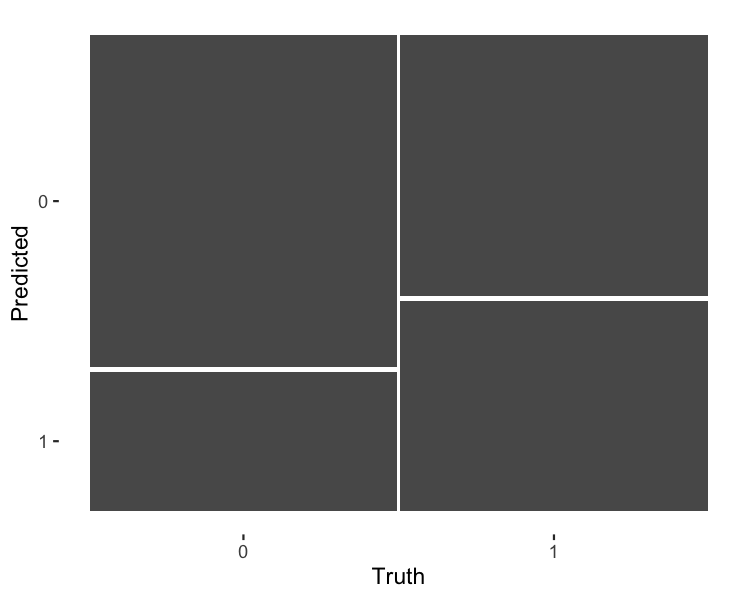
Visualisierung der Konfusionsmatrix: Mosaikdiagramm
library(ggplot2)
library(yardstick)
confusion <- conf_mat(outcomes)
actual_response
predicted_response 0 1
0 141 111
1 59 89
autoplot(confusion)
Leistungskennzahlen
summary(confusion, event_level = "second")
# A tibble: 13 x 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 accuracy binary 0.575
2 kap binary 0.150
3 sens binary 0.445
4 spec binary 0.705
5 ppv binary 0.601
6 npv binary 0.560
7 mcc binary 0.155
8 j_index binary 0.150
9 bal_accuracy binary 0.575
10 detection_prevalence binary 0.37
11 precision binary 0.601
12 recall binary 0.445
13 f_meas binary 0.511
Genauigkeit
summary(confusion) %>%
slice(1)
# A tibble: 3 x 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 accuracy binary 0.575
Genauigkeit entspricht dem Anteil der richtigen Vorhersagen.
$$ accuracy = \frac{TN + TP}{TN + FN + FP + TP} $$
confusion
actual_response
predicted_response 0 1
0 141 111
1 59 89
(141 + 89) / (141 + 111 + 59 + 89)
0.575
Empfindlichkeit
summary(confusion) %>%
slice(3)
# A tibble: 1 x 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 sens binary 0.445
Sensitivität entspricht dem Anteil der richtig positiven Ergebnisse.
$$ sensitivity = \frac{TP}{FN + TP} $$
confusion
actual_response
predicted_response 0 1
0 141 111
1 59 89
89 / (111 + 89)
0.445
Spezifität
summary(confusion) %>%
slice(4)
# A tibble: 1 x 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 spec binary 0.705
Spezifität entspricht dem Anteil der richtig negativen Ergebnisse.
$$ specificity = \frac{TN}{TN + FP} $$
confusion
actual_response
predicted_response 0 1
0 141 111
1 59 89
141 / (141 + 59)
0.705
Lass uns üben!
Einführung in Regression mit R

