Quantifizierung der Anpassungsgüte des Modells

Einführung in Regression mit R

Richie Cotton

Data Evangelist at DataCamp

Brassen- und Barschmodelle

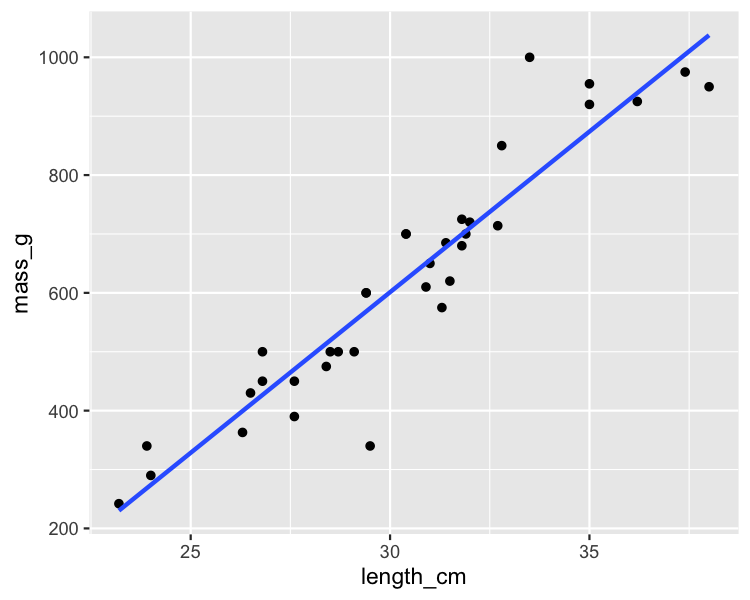
Brassen

Das Streudiagramm der Brassengewichte im Vergleich zu ihrer Länge mit einer Trendlinie, das schon mal gezeigt wurde.

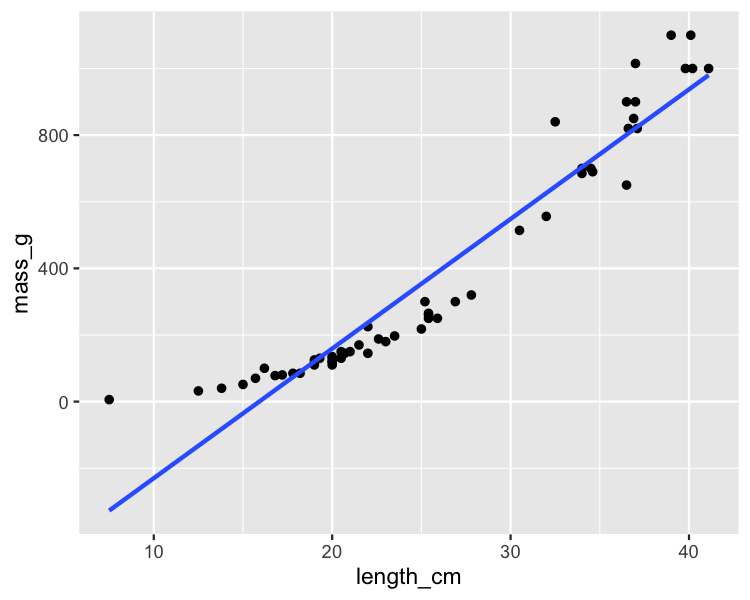
Barsch

Das Streudiagramm der Masse von Barschen im Vergleich zu ihrer Länge mit einer Trendlinie, das schon mal gezeigt wurde.

Bestimmtheitsmaß

Manchmal auch „r-squared“ oder „R-squared“ genannt.

Der Anteil der Varianz in der Antwortvariablen, der anhand der erklärenden Variablen vorhergesagt werden kann.

1 repräsentiert eine perfekte Passform
0 repräsentiert die schlechteste Passform

summary()

Schau dir den Wert namens „Multiple R-Squared” an.

mdl_bream <- lm(mass_g ~ length_cm, data = bream)

summary(mdl_bream)

# Some lines of output omitted

Residual standard error: 74.15 on 33 degrees of freedom
Multiple R-squared:  0.8781,    Adjusted R-squared:  0.8744 
F-statistic: 237.6 on 1 and 33 DF,  p-value: < 2.2e-16

glance()

library(broom)
library(dplyr)
mdl_bream %>% 
  glance()

# A tibble: 1 × 12
  r.squared adj.r.squared sigma statistic  p.value    df logLik   AIC   BIC
      <dbl>         <dbl> <dbl>     <dbl>    <dbl> <dbl>  <dbl> <dbl> <dbl>
1     0.878         0.874  74.2      238. 1.22e-16     1  -199.  405.  409.
# ... with 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>

mdl_bream %>% 
  glance() %>% 
  pull(r.squared)

0.8780627

Korrelationskoeffizient hoch zwei

bream %>% 
  summarize(
    coeff_determination = cor(length_cm, mass_g) ^ 2
  )

  coeff_determination
1           0.8780627

Standardfehler der Residuen (RSE = Residual Standard Error)

Der „typische“ Abstand zwischen einer Vorhersage und einer beobachteten Antwort

Hat die gleiche Einheit wie die Antwortvariable.

Erneut: summary()

Sieh dir den Wert mit dem Namen „Residual standard error” an.

summary(mdl_bream)

# Some lines of output omitted

Residual standard error: 74.15 on 33 degrees of freedom
Multiple R-squared:  0.8781,    Adjusted R-squared:  0.8744 
F-statistic: 237.6 on 1 and 33 DF,  p-value: < 2.2e-16

Erneut: glance()

library(broom)
library(dplyr)
mdl_bream %>% 
  glance()

# A tibble: 1 x 11
  r.squared adj.r.squared sigma statistic  p.value    df logLik   AIC   BIC deviance df.residual
      <dbl>         <dbl> <dbl>     <dbl>    <dbl> <int>  <dbl> <dbl> <dbl>    <dbl>       <int>
1     0.878         0.874  74.2      238. 1.22e-16     2  -199.  405.  409.  181452.          33

mdl_bream %>% 
  glance() %>% 
  pull(sigma)

74.15224

RSE-Berechnung: Residuen quadriert

bream %>% 
  mutate(
    residuals_sq = residuals(mdl_bream) ^ 2
  )

  species mass_g length_cm residuals_sq
1   Bream    242      23.2     138.9571
2   Bream    290      24.0     260.7586
3   Bream    340      23.9    5126.9926
4   Bream    363      26.3    1318.9197
5   Bream    430      26.5     390.9743
6   Bream    450      26.8     547.9380
...

RSE-Berechnung: Summe der quadrierten Residuen

bream %>% 
  mutate(
    residuals_sq = residuals(mdl_bream) ^ 2
  ) %>% 
  summarize(
    resid_sum_of_sq = sum(residuals_sq)
  )

  resid_sum_of_sq
1        181452.3

RSE-Berechnung: Freiheitsgrade

Degrees of freedom / Freiheitsgrade sind gleich der Anzahl der Beobachtungen minus der Anzahl der Modellkoeffizienten.

bream %>% 
  mutate(
    residuals_sq = residuals(mdl_bream) ^ 2
  ) %>% 
  summarize(
    resid_sum_of_sq = sum(residuals_sq),
    deg_freedom = n() - 2
  )

  resid_sum_of_sq deg_freedom
1        181452.3          33

RSE-Berechnung: Quadratwurzel des Verhältnisses

bream %>% 
  mutate(
    residuals_sq = residuals(mdl_bream) ^ 2
  ) %>% 
  summarize(
    resid_sum_of_sq = sum(residuals_sq),
    deg_freedom = n() - 2,
    rse = sqrt(resid_sum_of_sq / deg_freedom)
  )

  resid_sum_of_sq deg_freedom      rse
1        181452.3          33 74.15224

RSE interpretieren

mdl_bream hat einen RSE von 74.

Der Unterschied zwischen der vorhergesagten Brassenmasse und der tatsächlich gemessenen Brassenmasse ist normalerweise etwa 74 g.

Mittlere quadratische Abweichung (Root-mean-square error (RMSE))

Standardfehler der Residuen

bream %>% 
  mutate(
    residuals_sq = residuals(mdl_bream) ^ 2
  ) %>% 
  summarize(
    resid_sum_of_sq = sum(residuals_sq),
    deg_freedom = n() - 2,
    rse = sqrt(resid_sum_of_sq / deg_freedom)
  )

Mittlere quadratische Abweichung

bream %>% 
  mutate(
    residuals_sq = residuals(mdl_bream) ^ 2
  ) %>% 
  summarize(
    resid_sum_of_sq = sum(residuals_sq),
    n_obs = n(),
    rmse = sqrt(resid_sum_of_sq / n_obs)
  )

Lass uns üben!

Einführung in Regression mit R