Anpassen einer linearen Regression

Einführung in Regression mit R

Richie Cotton

Data Evangelist at DataCamp

Geraden werden durch zwei Eigenschaften definiert

Schnittpunkt

Der $y$-Wert für $x$ gleich Null.

Steigung

Der Wert, um den $y$ zunimmt, wenn $x$ um Eins erhöht wird.

Gleichung

$y = intercept + slope * x$

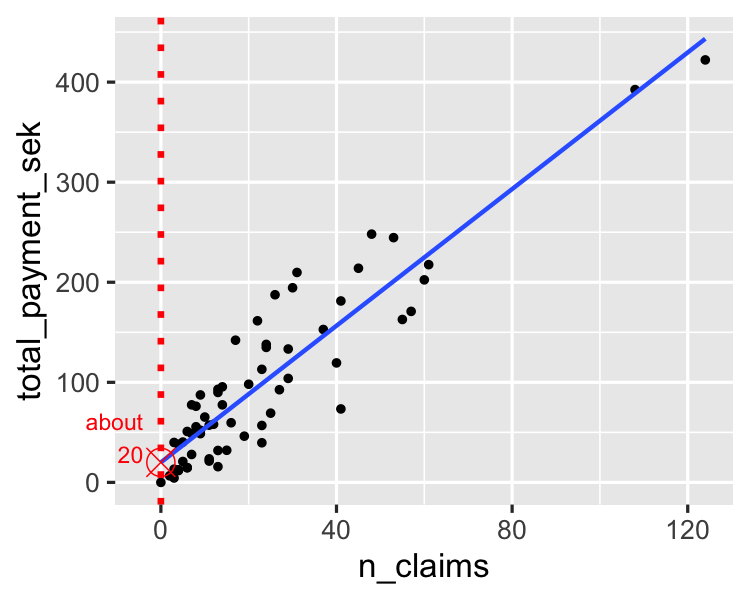
Den Schnittpunkt schätzen

Ein Streudiagramm der Gesamtzahlungen im Vergleich zur Anzahl der Schadensfälle mit einer linearen Trendlinie. Die Zahlung steigt linear mit der Anzahl der Ansprüche.

Den Schnittpunkt schätzen

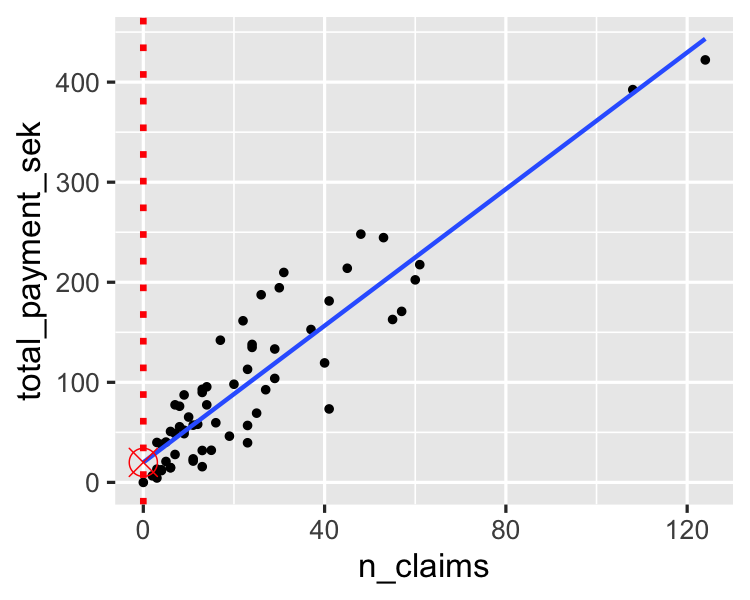
Das Streudiagramm der Gesamtzahlungen im Vergleich zur Anzahl der Schadensfälle, mit dem Punkt, an dem die Trendlinie die y-Achse schneidet.

Den Schnittpunkt schätzen

Das Streudiagramm der Gesamtzahlung im Vergleich zur Anzahl der Schadensfälle, mit dem Wert versehen, wenn die Anzahl der Schadensfälle null ist.

Die Steigung schätzen

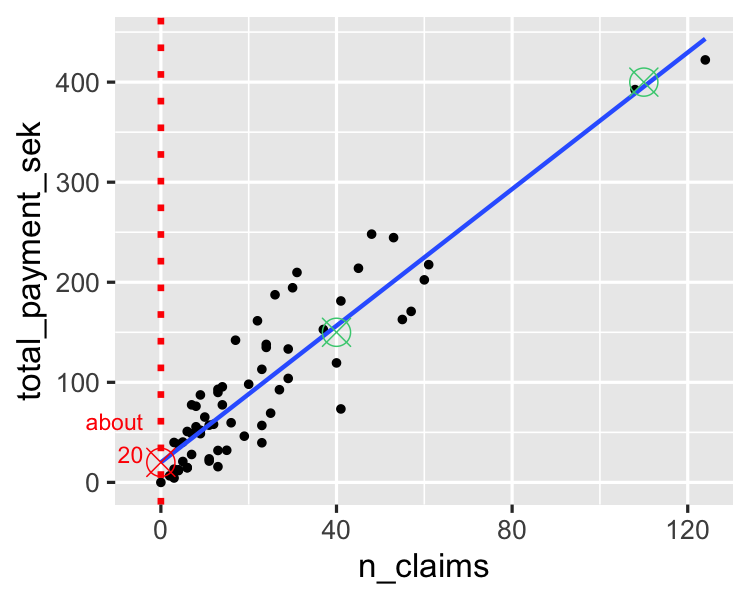
Das Streudiagramm der Gesamtzahlungen im Vergleich zur Anzahl der Schadensfälle, mit zwei Punkten auf der Trendlinie. Ein Punkt liegt bei 150 Kronen und 40 Ansprüchen, ein anderer Punkt bei 400 Kronen und 110 Ansprüchen.

Die Steigung schätzen

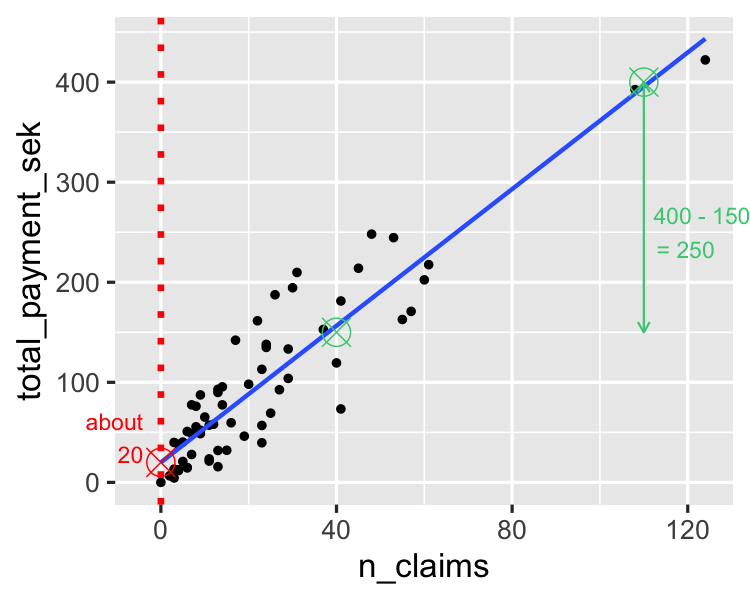
Das Streudiagramm der Gesamtzahlungen im Vergleich zur Anzahl der Schadensfälle, mit den Zahlungsunterschieden zwischen den beiden Punkten. 400 Kronen minus 150 Kronen sind 250 Kronen.

Die Steigung schätzen

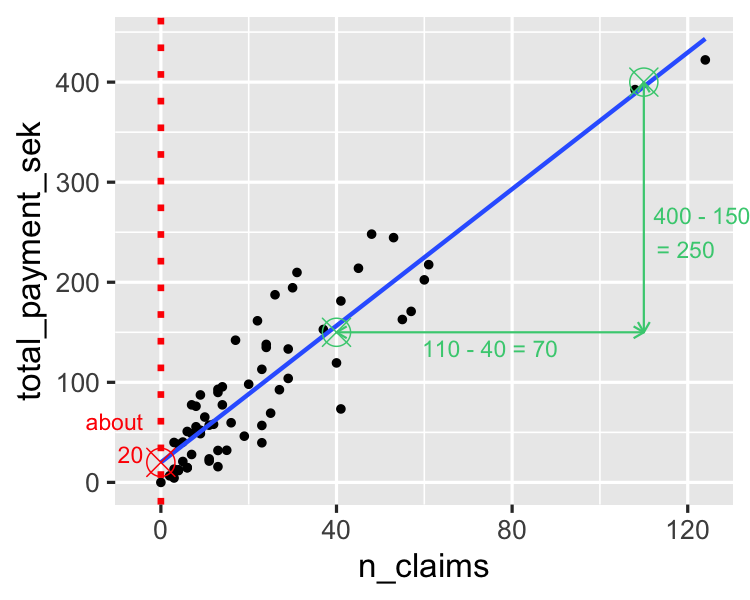
Das Streudiagramm der Gesamtzahlungen im Vergleich zur Anzahl der Schadensfälle, mit Anmerkungen zur Differenz in der Anzahl der Schadensfälle zwischen den beiden Punkten. 110 Ansprüche minus 40 Ansprüche sind 70 Ansprüche.

Die Steigung schätzen

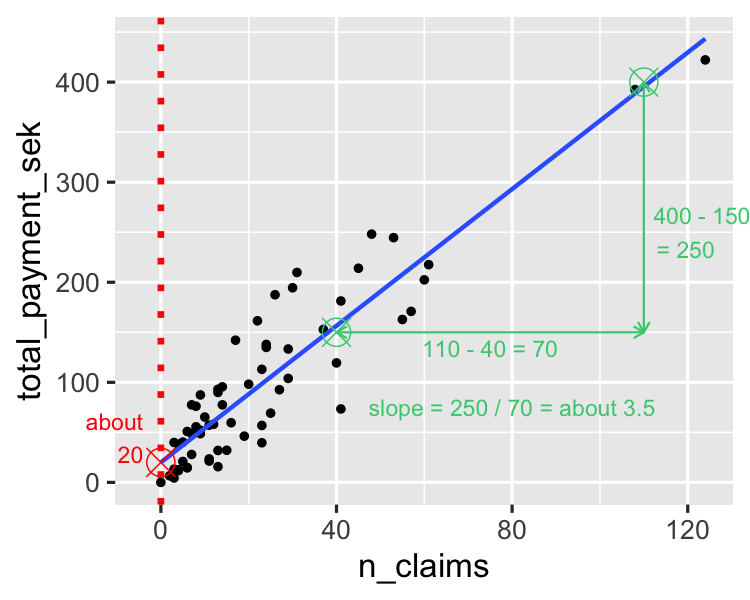
Das Streudiagramm der Gesamtzahlungen im Vergleich zur Anzahl der Schadensfälle, mit Anmerkungen zum Verhältnis von Differenz und Zahlung sowie zur Differenz in der Anzahl der Schadensfälle. 2000 geteilt durch 60 ist ungefähr 33.

Ein Modell ausführen

lm(total_payment_sek ~ n_claims, data = swedish_motor_insurance)

Call:
lm(formula = total_payment_sek ~ n_claims, data = swedish_motor_insurance)

Coefficients:
(Intercept)     n_claims  
     19.994        3.414

Interpretation der Modellkoeffizienten

Call:
lm(formula = total_payment_sek ~ n_claims, data = swedish_motor_insurance)

Coefficients:
(Intercept)     n_claims  
     19.994        3.414

Gleichung

$total\_payment\_sek = 19.994 + 3.414 * n\_claims$

Lass uns üben!

Einführung in Regression mit R