Prognosen und Chancenverhältnis

Einführung in Regression mit R

Richie Cotton

Data Evangelist at DataCamp

Vorhersagen mit ggplot

plt_churn_vs_recency_base <- ggplot(
  churn, 
  aes(time_since_last_purchase, has_churned)
) +
  geom_point() +
  geom_smooth(
    method = "glm", 
    se = FALSE, 
    method.args = list(family = binomial)
  )

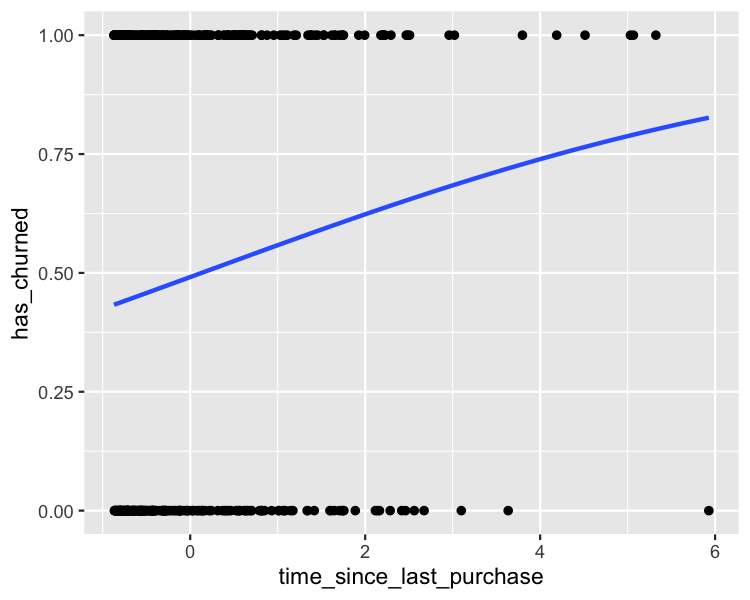
Ein Streudiagramm, das die Abwanderung im Vergleich zur Zeit seit dem letzten Kauf zeigt, mit einer logistischen Trendlinie.

Vorhersagen

mdl_recency <- glm(
  has_churned ~ time_since_last_purchase, data = churn, family = "binomial"
)

explanatory_data <- tibble(
  time_since_last_purchase = seq(-1, 6, 0.25)
)

prediction_data <- explanatory_data %>% 
  mutate(
    has_churned = predict(mdl_recency, explanatory_data, type = "response")
  )

Punktprognosen hinzufügen

plt_churn_vs_recency_base +
  geom_point(
    data = prediction_data, 
    color = "blue"
  )

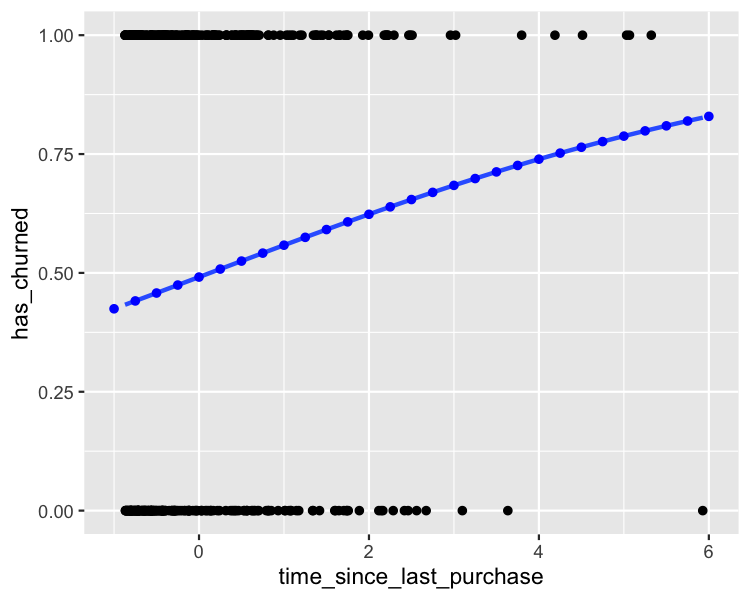
Das Streudiagramm der Abwanderung im Vergleich zur Zeit seit dem letzten Kauf, mit einer logistischen Trendlinie. Die Grafik zeigt die Ergebnisse von predict(), die genau der Trendlinie folgen.

Das wahrscheinlichste Ergebnis ermitteln

prediction_data <- explanatory_data %>% 
  mutate(
    has_churned = predict(mdl_recency, explanatory_data, type = "response"),
    most_likely_outcome = round(has_churned)
  )

Das wahrscheinlichste Ergebnis visualisieren

plt_churn_vs_recency_base +
  geom_point(
    aes(y = most_likely_outcome),
    data = prediction_data,
    color = "green"
  )

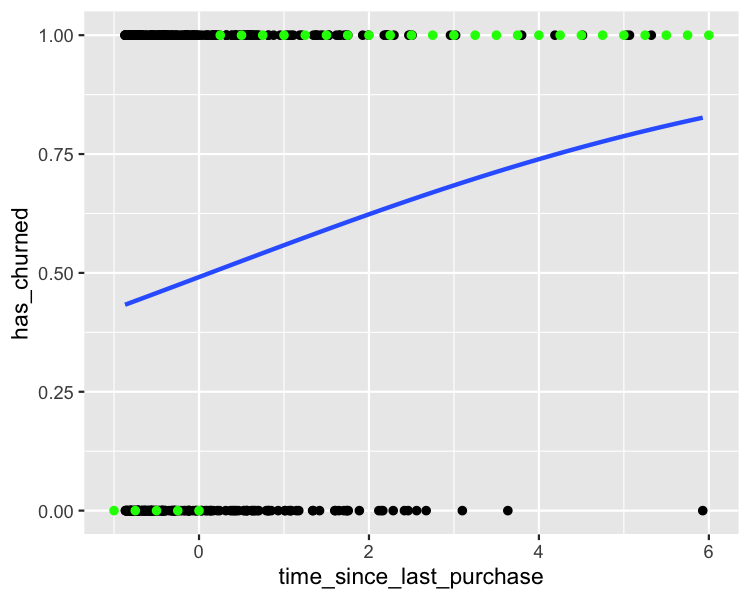
Das Streudiagramm der Abwanderung im Vergleich zur Zeit seit dem letzten Kauf, mit einer logistischen Trendlinie. Die Grafik zeigt die wahrscheinlichsten Ergebnisse. Wenn seit dem letzten Kauf nicht viel Zeit vergangen ist, ist es ziemlich unwahrscheinlich, dass du den Anbieter wechselst. Wenn seit dem letzten Kauf schon viel Zeit vergangen ist, ist das wahrscheinlichste Ergebnis eine Abwanderung.

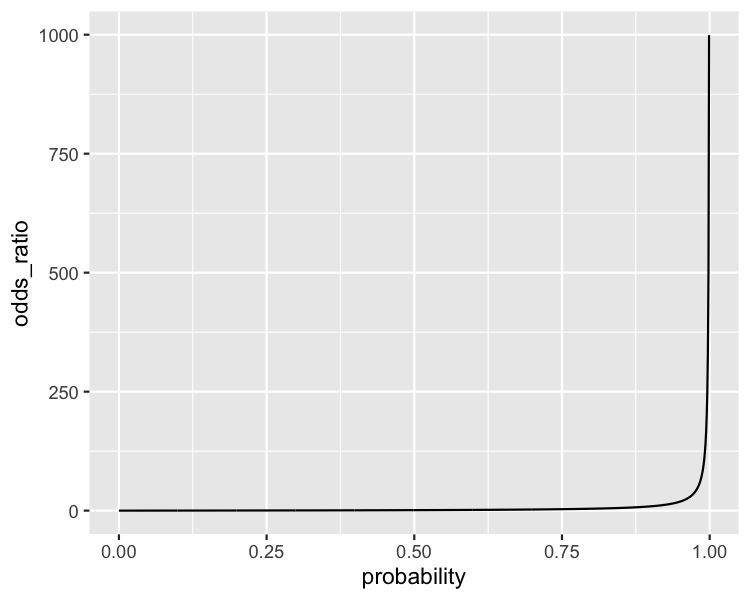
Odds ratios (Chancenverhältnis)

Odds Ratio (Chancenverhältnis) ist die Wahrscheinlichkeit, dass etwas passiert, geteilt durch die Wahrscheinlichkeit, dass es nicht passiert

$$ odds\_ratio = \frac{probability}{(1 - probability)} $$

$$ odds_ratio = \frac{0,25}{(1 - 0,25)} = \frac{1}{3} $$

Ein Liniendiagramm, das die Odds Ratio gegen die Wahrscheinlichkeit zeigt. Die Kurve steigt unendlich, wenn die Wahrscheinlichkeit gegen eins geht.

Berechnung der odds ratio

prediction_data <- explanatory_data %>%
  mutate(
    has_churned = predict(mdl_recency, explanatory_data, type = "response"),
    most_likely_response = round(has_churned),
    odds_ratio = has_churned / (1 - has_churned)
  )

Visualisierung der odds ratio

ggplot(
  prediction_data, 
  aes(time_since_last_purchase, odds_ratio)
) +
  geom_line() +
  geom_hline(yintercept = 1, linetype = "dotted")

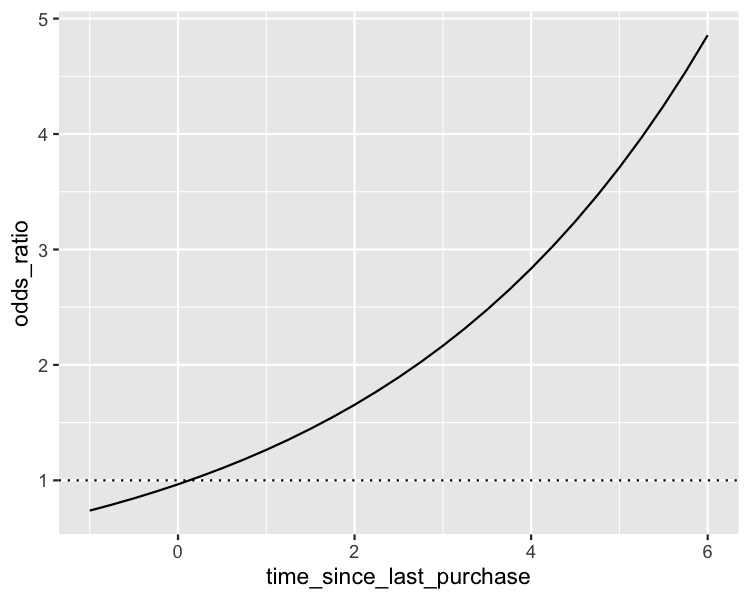
Visualisierung der log odds ratio

ggplot(
  prediction_data, 
  aes(time_since_last_purchase, odds_ratio)
) +
  geom_line() +
  geom_hline(yintercept = 1, linetype = "dotted") +
  scale_y_log10()

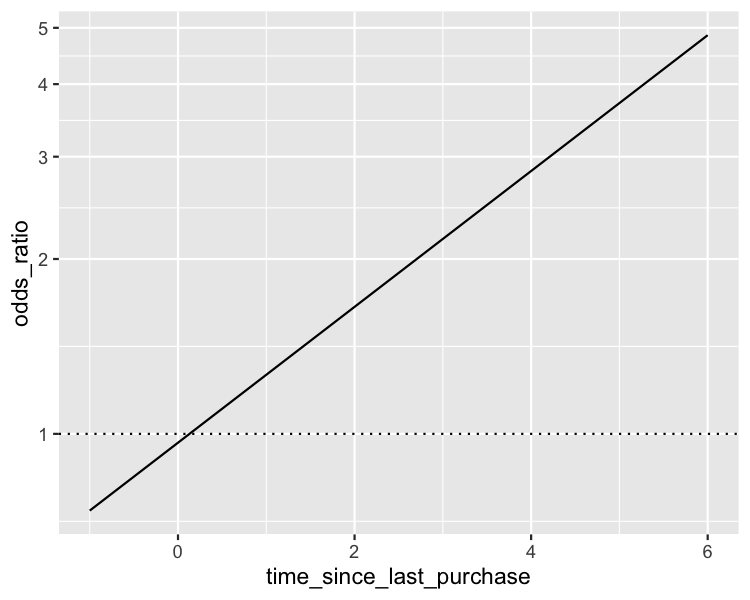
Das Liniendiagramm zeigt das Verhältnis der Wahrscheinlichkeiten im Vergleich zur Zeit seit dem letzten Kauf, mit einer Linie bei einem Verhältnis von eins. Die y-Achse hat 'ne logarithmische Skala, was dazu führt, dass die Odds-Ratio-Linie linear wird.

Das log-odds-ratio berechnen

prediction_data <- explanatory_data %>%
  mutate(
    has_churned = predict(mdl_recency, explanatory_data, type = "response"),
    most_likely_response = round(has_churned),
    odds_ratio = has_churned / (1 - has_churned),
    log_odds_ratio = log(odds_ratio),
    log_odds_ratio2 = predict(mdl_recency, explanatory_data)
  )

Alle Vorhersagen

tm_snc_lst_prch	has_churned	most_lkly_rspns	odds_ratio	log_odds_ratio	log_odds_ratio2
0	0,491	0	0,966	-0,035	-0,035
2	0,623	1	1,654	0,503	0,503
4	0,739	1	2,834	1,042	1,042
6	0,829	1	4,856	1,580	1,580
...	...	...	...	...	...

Skalen vergleichen

Skala	Sind Werte leicht zu verstehen?	Sind Veränderungen leicht zu verstehen?	Präzise?
Wahrscheinlichkeit	✔	✘	✔
Wahrscheinlichstes Ergebnis	✔✔	✔	✘
Odds-ratio	✔	✘	✔
Log-odds-ratio	✘	✔	✔

Lass uns üben!

Einführung in Regression mit R