Quantification de l'ajustement du modèle

Introduction à la régression dans R

Richie Cotton

Data Evangelist at DataCamp

Modèles de brèmes communes et de perches

Brème commune

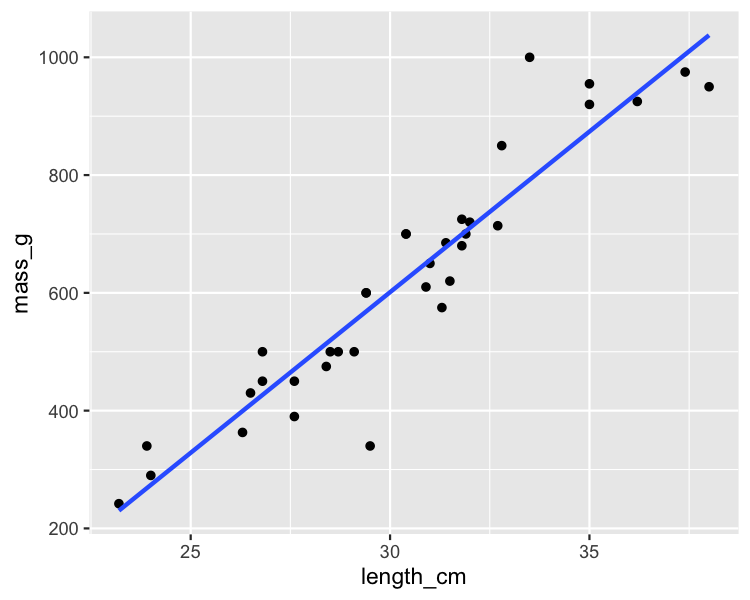
Le diagramme en nuage de points représentant le rapport entre la masse et la longueur des brèmes communes, avec une courbe de tendance, qui a été présenté précédemment.

Perche

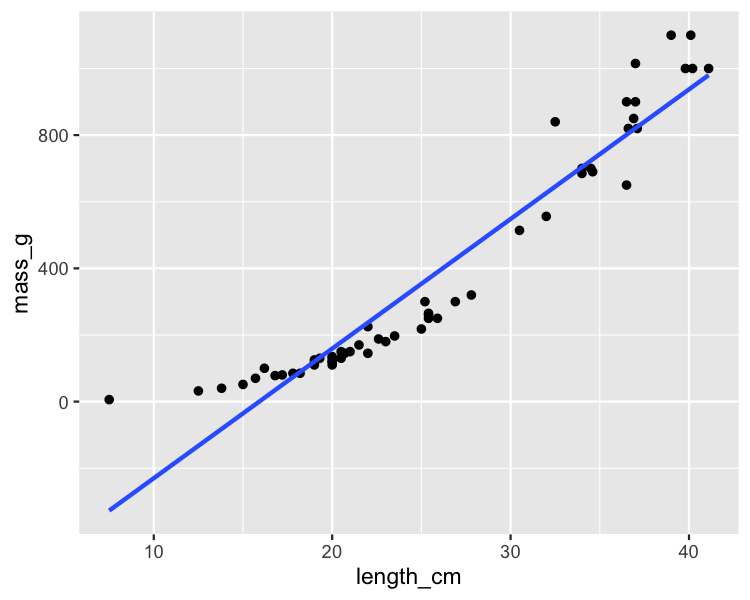
Le diagramme en nuage de points représentant le poids des perches en fonction de leur longueur, avec une courbe de tendance, qui a été présenté précédemment.

Introduction à la régression dans R

Coefficient de détermination

Parfois appelé « r au carré » ou « R au carré ».

la proportion de la variance de la variable de réponse qui est prévisible à partir de la variable explicative

  • 1 signifie un ajustement parfait
  • 0 signifie le pire ajustement possible
Introduction à la régression dans R

summary()

Examiner la valeur intitulée « R-carré multiple ».

mdl_bream <- lm(mass_g ~ length_cm, data = bream)

summary(mdl_bream)

# Some lines of output omitted

Residual standard error: 74.15 on 33 degrees of freedom
Multiple R-squared:  0.8781,    Adjusted R-squared:  0.8744 
F-statistic: 237.6 on 1 and 33 DF,  p-value: < 2.2e-16
Introduction à la régression dans R

glance()

library(broom)
library(dplyr)
mdl_bream %>% 
  glance()

# A tibble: 1 × 12
  r.squared adj.r.squared sigma statistic  p.value    df logLik   AIC   BIC
      <dbl>         <dbl> <dbl>     <dbl>    <dbl> <dbl>  <dbl> <dbl> <dbl>
1     0.878         0.874  74.2      238. 1.22e-16     1  -199.  405.  409.
# ... with 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>

mdl_bream %>% 
  glance() %>% 
  pull(r.squared)

0.8780627
Introduction à la régression dans R

Il s'agit simplement d'une corrélation au carré.

bream %>% 
  summarize(
    coeff_determination = cor(length_cm, mass_g) ^ 2
  )

  coeff_determination
1           0.8780627
Introduction à la régression dans R

Erreur type résiduelle (ETR)

une différence « typique » entre une prédiction et une réponse observée

Elle a la même unité que la variable de réponse.

Introduction à la régression dans R

summary() à nouveau

Veuillez examiner la valeur intitulée « Erreur type résiduelle ».

summary(mdl_bream)

# Some lines of output omitted

Residual standard error: 74.15 on 33 degrees of freedom
Multiple R-squared:  0.8781,    Adjusted R-squared:  0.8744 
F-statistic: 237.6 on 1 and 33 DF,  p-value: < 2.2e-16
Introduction à la régression dans R

glance() à nouveau

library(broom)
library(dplyr)
mdl_bream %>% 
  glance()

# A tibble: 1 x 11
  r.squared adj.r.squared sigma statistic  p.value    df logLik   AIC   BIC deviance df.residual
      <dbl>         <dbl> <dbl>     <dbl>    <dbl> <int>  <dbl> <dbl> <dbl>    <dbl>       <int>
1     0.878         0.874  74.2      238. 1.22e-16     2  -199.  405.  409.  181452.          33

mdl_bream %>% 
  glance() %>% 
  pull(sigma)

74.15224
Introduction à la régression dans R

Calcul du RSE : résidus au carré

bream %>% 
  mutate(
    residuals_sq = residuals(mdl_bream) ^ 2
  )

  species mass_g length_cm residuals_sq
1   Bream    242      23.2     138.9571
2   Bream    290      24.0     260.7586
3   Bream    340      23.9    5126.9926
4   Bream    363      26.3    1318.9197
5   Bream    430      26.5     390.9743
6   Bream    450      26.8     547.9380
...
Introduction à la régression dans R

Calcul du RSE : somme des résidus au carré

bream %>% 
  mutate(
    residuals_sq = residuals(mdl_bream) ^ 2
  ) %>% 
  summarize(
    resid_sum_of_sq = sum(residuals_sq)
  )

  resid_sum_of_sq
1        181452.3
Introduction à la régression dans R

Calcul du RSE : degrés de liberté

Le nombre de degrés de liberté correspond au nombre d'observations moins le nombre de coefficients du modèle.

bream %>% 
  mutate(
    residuals_sq = residuals(mdl_bream) ^ 2
  ) %>% 
  summarize(
    resid_sum_of_sq = sum(residuals_sq),
    deg_freedom = n() - 2
  )

  resid_sum_of_sq deg_freedom
1        181452.3          33
Introduction à la régression dans R

Calcul du RSE : racine carrée du rapport

bream %>% 
  mutate(
    residuals_sq = residuals(mdl_bream) ^ 2
  ) %>% 
  summarize(
    resid_sum_of_sq = sum(residuals_sq),
    deg_freedom = n() - 2,
    rse = sqrt(resid_sum_of_sq / deg_freedom)
  )

  resid_sum_of_sq deg_freedom      rse
1        181452.3          33 74.15224
Introduction à la régression dans R

Interprétation de la RSE

mdl_bream a un RSE de 74.

La différence entre les masses prévues et les masses observées pour les brèmes communes est généralement d'environ 74 g.

Introduction à la régression dans R

Erreur quadratique moyenne (RMSE)

Erreur type résiduelle

bream %>% 
  mutate(
    residuals_sq = residuals(mdl_bream) ^ 2
  ) %>% 
  summarize(
    resid_sum_of_sq = sum(residuals_sq),
    deg_freedom = n() - 2,
    rse = sqrt(resid_sum_of_sq / deg_freedom)
  )

Erreur quadratique moyenne

bream %>% 
  mutate(
    residuals_sq = residuals(mdl_bream) ^ 2
  ) %>% 
  summarize(
    resid_sum_of_sq = sum(residuals_sq),
    n_obs = n(),
    rmse = sqrt(resid_sum_of_sq / n_obs)
  )
Introduction à la régression dans R

Passons à la pratique !

Introduction à la régression dans R

Preparing Video For Download...