Prévisions et rapports de cotes

Introduction à la régression dans R

Richie Cotton

Data Evangelist at DataCamp

Les prévisions ggplot

plt_churn_vs_recency_base <- ggplot(
  churn, 
  aes(time_since_last_purchase, has_churned)
) +
  geom_point() +
  geom_smooth(
    method = "glm", 
    se = FALSE, 
    method.args = list(family = binomial)
  )

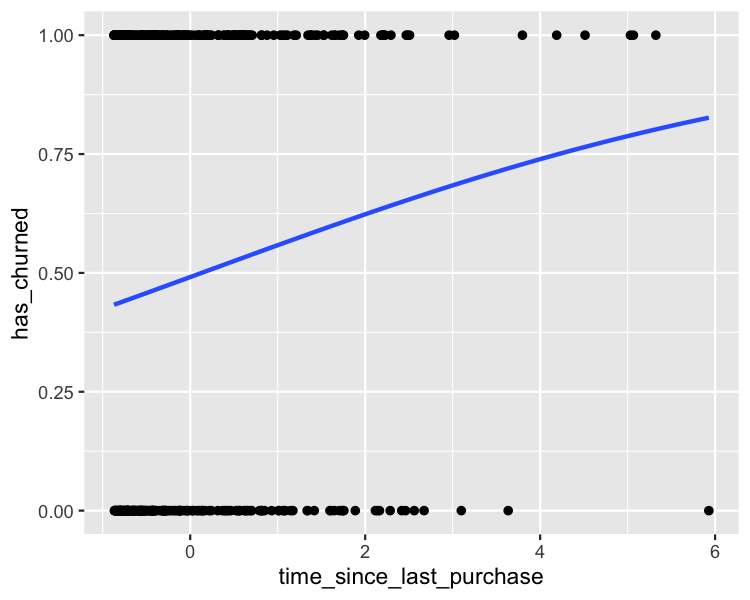
Diagramme en nuage de points représentant l’attrition en fonction du temps écoulé depuis le dernier achat, avec une courbe de tendance logistique.

Introduction à la régression dans R

Faire des prévisions

mdl_recency <- glm(
  has_churned ~ time_since_last_purchase, data = churn, family = "binomial"
)

explanatory_data <- tibble(
  time_since_last_purchase = seq(-1, 6, 0.25)
)

prediction_data <- explanatory_data %>% 
  mutate(
    has_churned = predict(mdl_recency, explanatory_data, type = "response")
  )
Introduction à la régression dans R

Ajout de prévisions de points

plt_churn_vs_recency_base +
  geom_point(
    data = prediction_data, 
    color = "blue"
  )

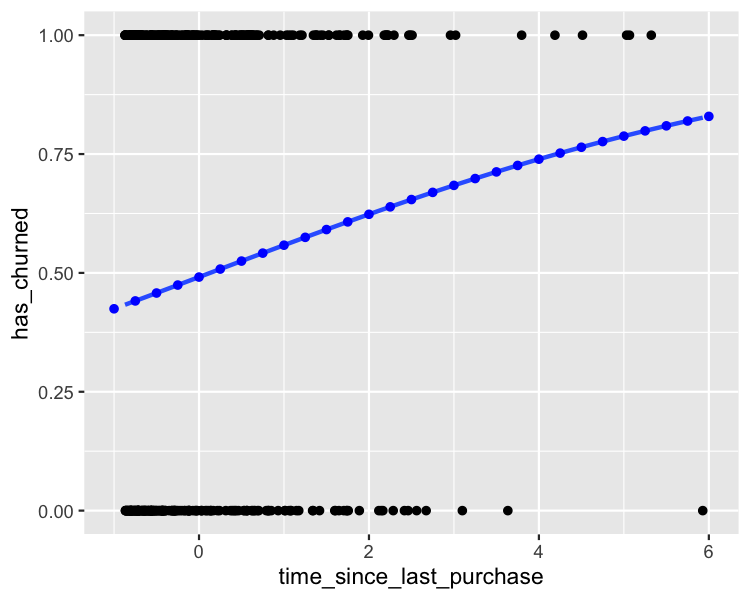
Le diagramme en nuage de points représentant l’attrition en fonction du temps écoulé depuis le dernier achat, avec une courbe de tendance logistique. Le graphique est annoté avec les résultats de predict(), qui suivent exactement la courbe de tendance.

Introduction à la régression dans R

Obtenir le résultat le plus probable

prediction_data <- explanatory_data %>% 
  mutate(
    has_churned = predict(mdl_recency, explanatory_data, type = "response"),
    most_likely_outcome = round(has_churned)
  )
Introduction à la régression dans R

Visualisation du résultat le plus probable

plt_churn_vs_recency_base +
  geom_point(
    aes(y = most_likely_outcome),
    data = prediction_data,
    color = "green"
  )

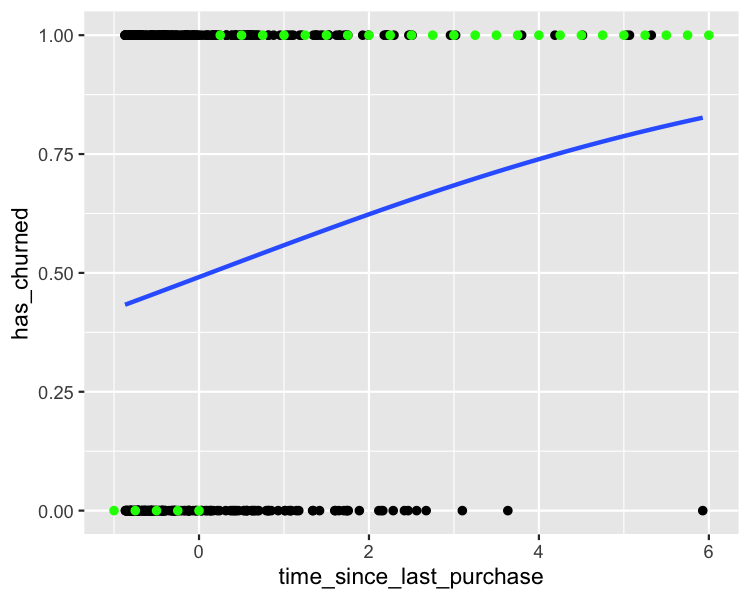
Le diagramme en nuage de points représentant l’attrition en fonction du temps écoulé depuis le dernier achat, avec une courbe de tendance logistique. Le graphique est annoté avec les résultats les plus probables. Si peu de temps s'est écoulé depuis le dernier achat, le résultat le plus probable est l'absence d’attrition. Si le dernier achat remonte à longtemps, le résultat le plus probable est l’attrition.

Introduction à la régression dans R

Rapports de cotes

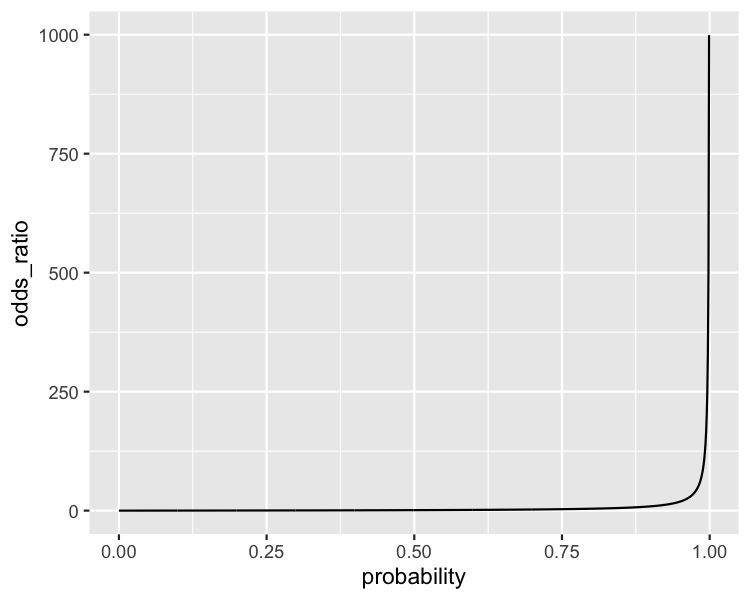
Le rapport de cotes est la probabilité qu'un événement se produise divisée par la probabilité qu'il ne se produise pas.

$$ odds\_ratio = \frac{probability}{(1 - probability)} $$

$$ cotes_ratio = \frac{0,25}{(1 - 0,25)} = \frac{1}{3} $$

Graphique linéaire représentant le rapport de cotes par rapport à la probabilité. La courbe augmente de manière asymptotique vers l'infini à mesure que la probabilité tend vers un.

Introduction à la régression dans R

Calcul du rapport de cotes

prediction_data <- explanatory_data %>%
  mutate(
    has_churned = predict(mdl_recency, explanatory_data, type = "response"),
    most_likely_response = round(has_churned),
    odds_ratio = has_churned / (1 - has_churned)
  )
Introduction à la régression dans R

Visualisation du rapport de cotes

ggplot(
  prediction_data, 
  aes(time_since_last_purchase, odds_ratio)
) +
  geom_line() +
  geom_hline(yintercept = 1, linetype = "dotted")

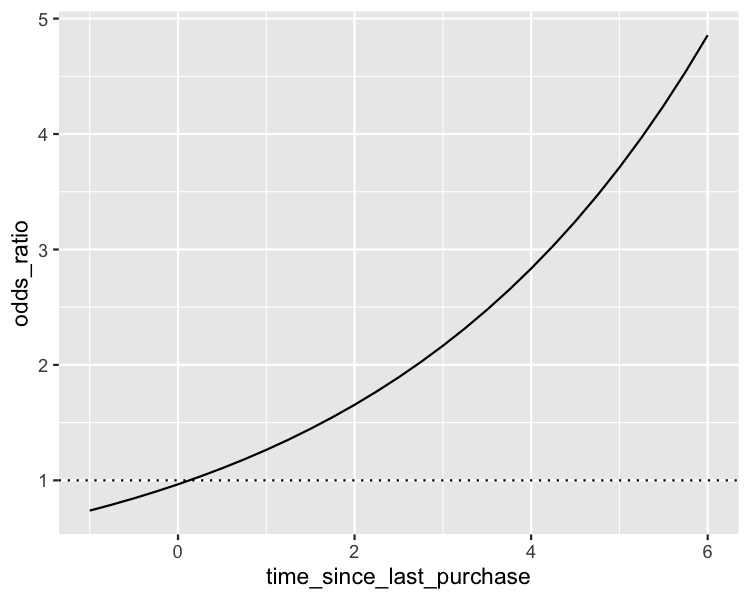
Graphique linéaire représentant le rapport de cotes en fonction du temps écoulé depuis le dernier achat, avec une ligne correspondant à un rapport de cotes égal à un. Si peu de temps s'est écoulé depuis le dernier achat, le résultat le plus probable est l'absence d’attrition. Les risques d’attrition augmentent à mesure que le temps écoulé depuis le dernier achat s'allonge, jusqu'à atteindre cinq fois les chances de fidélisation.

Introduction à la régression dans R

Visualisation du rapport de cotes logarithmique

ggplot(
  prediction_data, 
  aes(time_since_last_purchase, odds_ratio)
) +
  geom_line() +
  geom_hline(yintercept = 1, linetype = "dotted") +
  scale_y_log10()

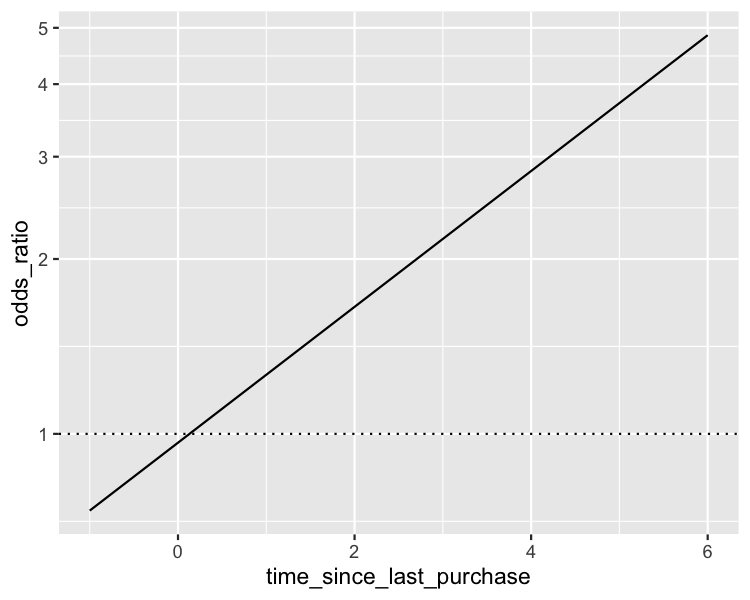
Le graphique linéaire représentant le rapport de cotes en fonction du temps écoulé depuis le dernier achat, avec une ligne correspondant à un rapport de cotes égal à un. L'axe des y utilise une échelle logarithmique, ce qui a pour conséquence de rendre la courbe du rapport de cotes linéaire.

Introduction à la régression dans R

Calcul du rapport de cotes logarithmique

prediction_data <- explanatory_data %>%
  mutate(
    has_churned = predict(mdl_recency, explanatory_data, type = "response"),
    most_likely_response = round(has_churned),
    odds_ratio = has_churned / (1 - has_churned),
    log_odds_ratio = log(odds_ratio),
    log_odds_ratio2 = predict(mdl_recency, explanatory_data)
  )
Introduction à la régression dans R

Toutes les prévisions réunies

tm_snc_lst_prch as_churned most_lkly_rspns odds_ratio log_odds_ratio log_odds_ratio2
0 0,491 0 0,966 -0,035 -0,035
2 0,623 1 1,654 0,503 0,503
4 0,739 1 2,834 1,042 1,042
6 0,829 1 4,856 1,580 1,580
... ... ... ... ... ...
Introduction à la régression dans R

Comparaison des échelles

Faire évoluer Les valeurs sont-elles faciles à interpréter ? Les modifications sont-elles faciles à interpréter ? Est-ce exact ?
Probabilité ✔ ✘ ✔
Résultat le plus probable ✔✔ ✔ ✘
Rapport de cotes ✔ ✘ ✔
Rapport de cotes logarithmique ✘ ✔ ✔
Introduction à la régression dans R

Passons à la pratique !

Introduction à la régression dans R

Preparing Video For Download...