t-interval for paired data

Inference for Numerical Data in R

Mine Cetinkaya-Rundel

Associate Professor of the Practice, Duke University

High School and Beyond

200 observations were randomly sampled from the High School and Beyond survey.The same students took a reading and writing test. At a first glance, how are the distributions of reading and writing scores similar? How are they different?

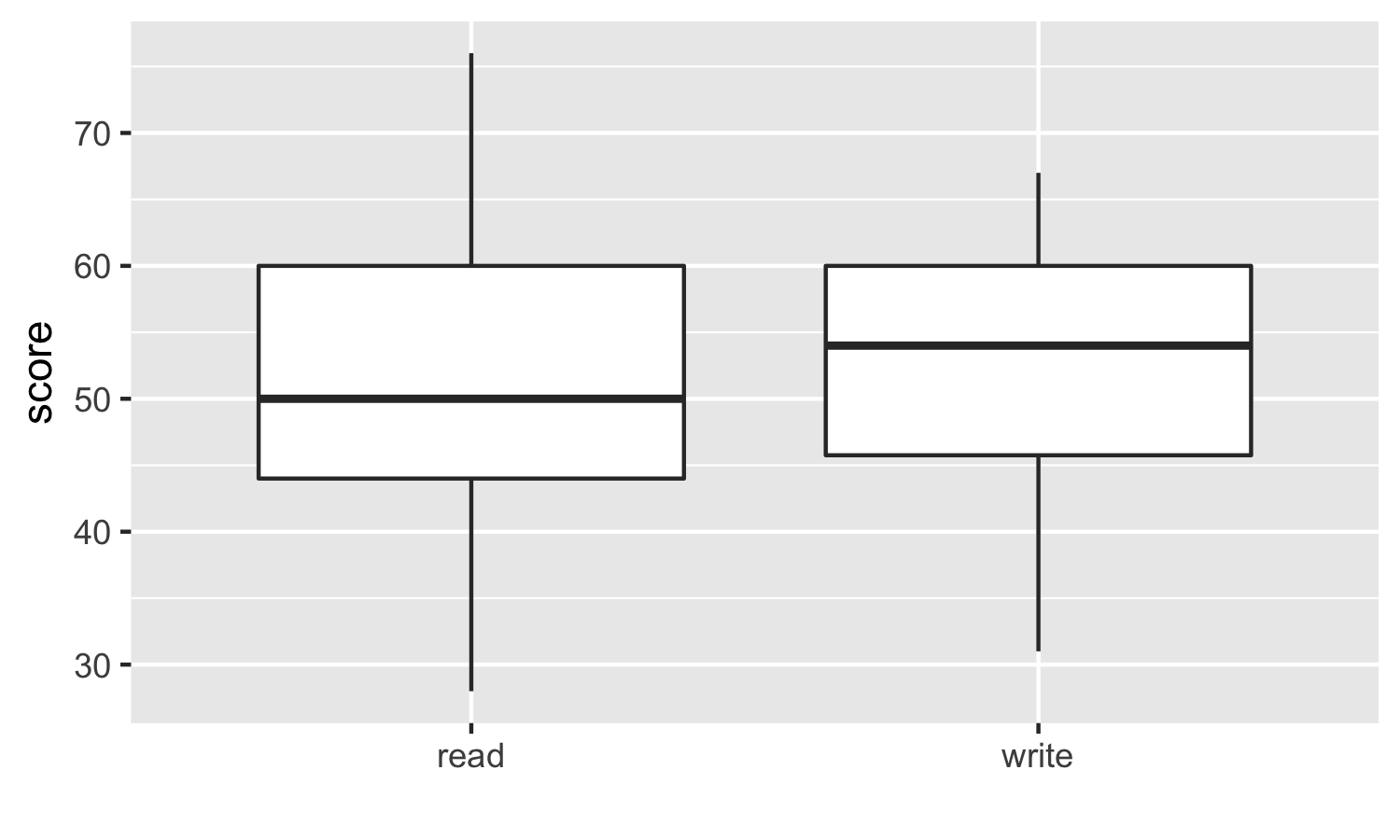
chp2-vid2-hsb2

Independent scores?

Can reading and writing scores for a given student student assumed to be independent of each other?

Probably not!

Analyzing paired data

When two sets of observations have this special correspondence (not independent), they are said to be paired.
To analyze paired data, it is often useful to look at the difference in outcomes of each pair of observations: diff = read ? write.

student	read	write	diff
1	57	52	5
2	68	59	9
3	44	33	11
...	...	...	...
200	63	65	-2

Estimating the mean difference in paired data

Construct a 95% confidence interval for the mean difference between the average reading and writing scores.

Estimating the mean difference in paired data

Construct a 95% confidence interval for the mean difference between the average reading and writing scores.

t.test(hsb2$diff, conf.level = 0.95)

Estimating the mean difference in paired data

Construct a 95% confidence interval for the mean difference between the average reading and writing scores.

t.test(hsb2$diff, conf.level = 0.95)

    One Sample t-test
data:  hsb2$diff
t = -0.86731, df = 199, p-value = 0.3868
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 -1.7841424  0.6941424
sample estimates:
mean of x 
   -0.545

Interpreting the CI for mean difference in paired data

95% CI for the mean difference in reading and writing scores (read - write) is (-1.78, 0.69)

vs.

We are 95% confident that the average reading score is 1.78 points lower to 0.69 points higher than the average writing score.

Let's practice!

Inference for Numerical Data in R