Probability rules

Fundamentals of Bayesian Data Analysis in R

Rasmus Bååth

Data Scientist

Bad and good news

• Bad news
  • The computation method we've used scales horribly.
• Good news
  • Bayesian computation is a hot research topic.
  • There are many methods to fit Bayesian models more efficiently.
  • The result will be the same, you'll just get it faster.

Probability theory

• Probability
  • A number between 0 and 1.
  • A statement of certainty/uncertainy.
• Mathematical notation:
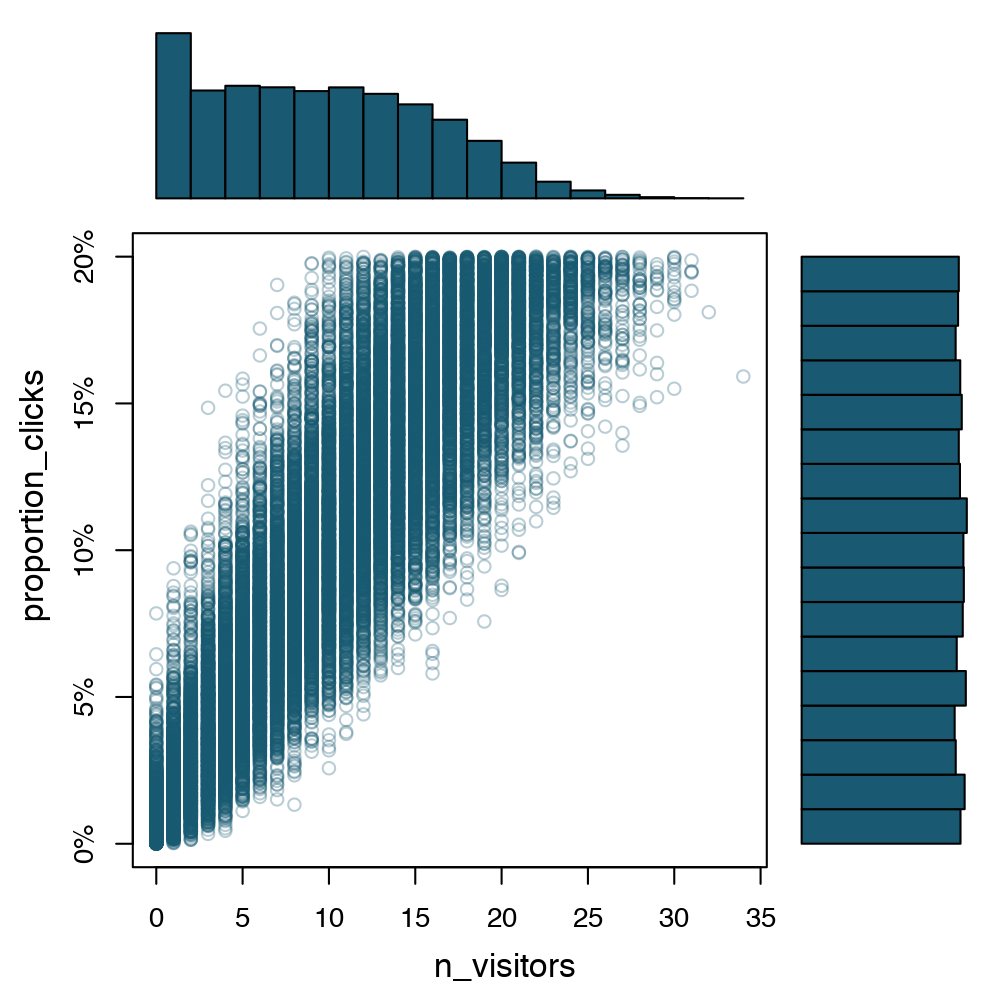
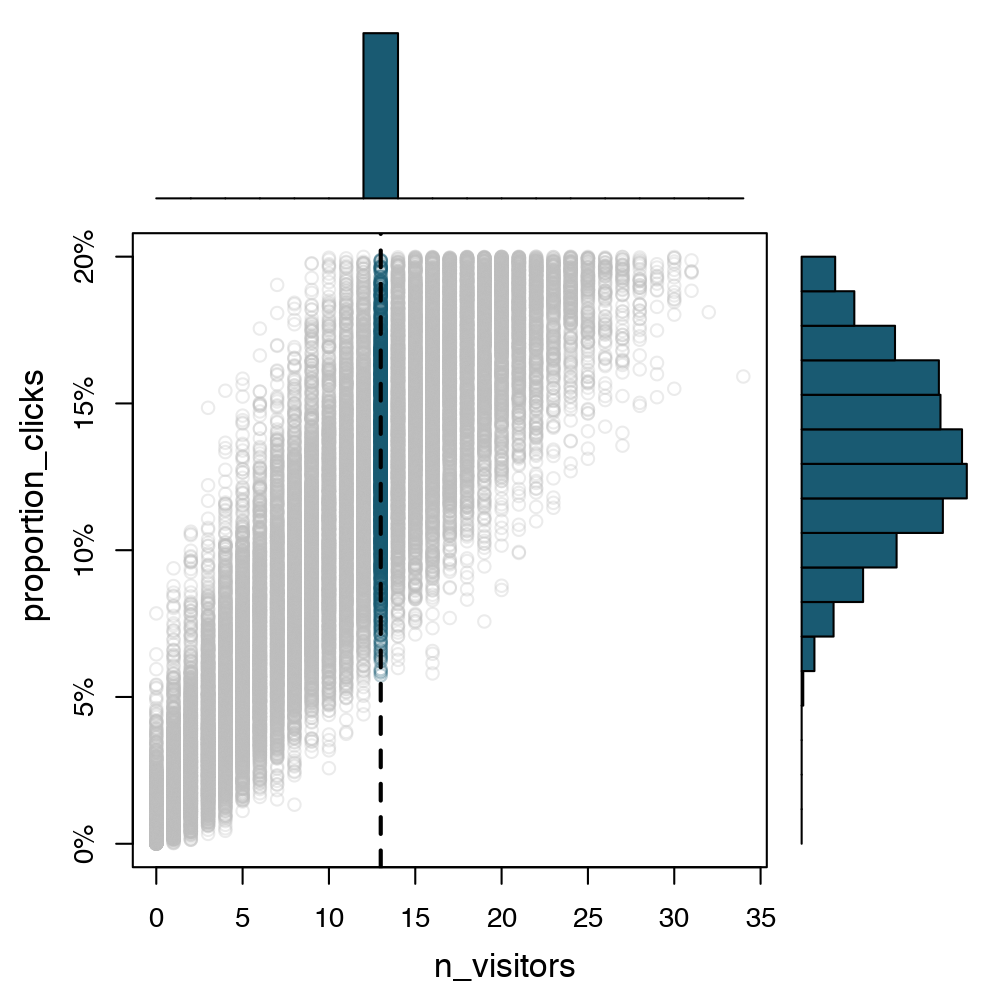
  • P(n_visitors = 13) is a probability
  • P(n_visitors) is a probability distribution
  • P(n_visitors = 13 | prop_clicks = 10%) is a conditional probability
  • P(n_visitors | prop_clicks = 10%) is a conditional probability distribution

P(n_visitors | prop_clicks = 10%)

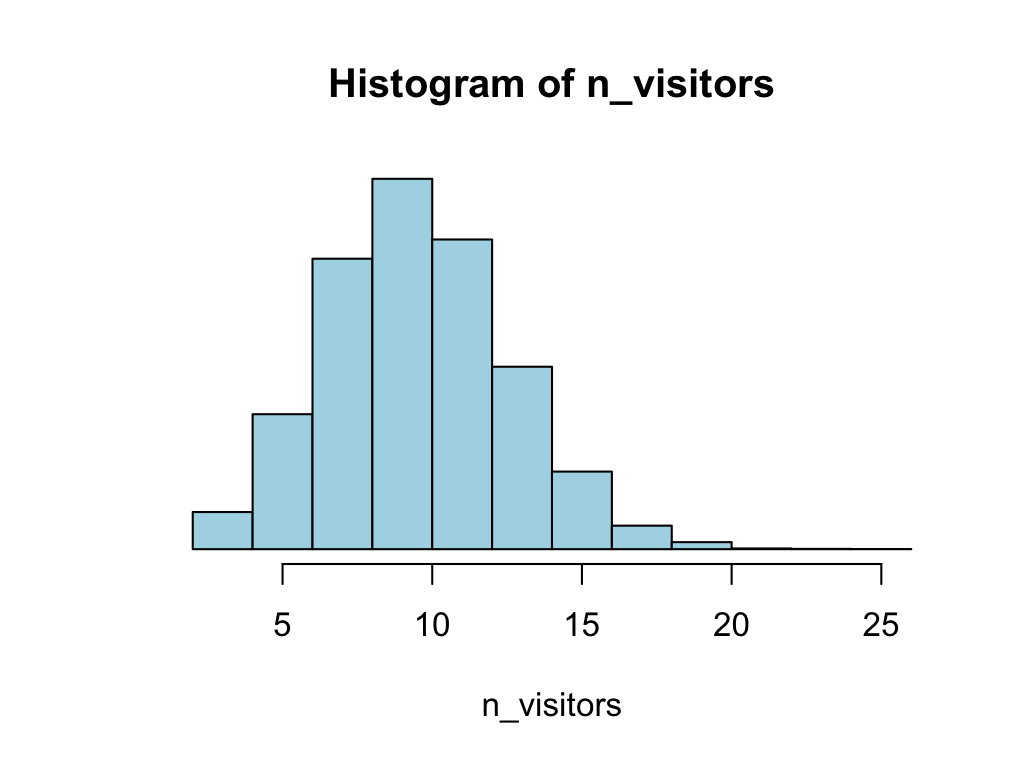
n_visitors <- rbinom(n = 10000, size = 100, prob = 0.1)
hist(n_visitors)

Manipulating probability

Manipulating probability

• The sum rule

Manipulating probability

• The sum rule
  • p(1 or 2 or 3)

Manipulating probability

• The sum rule
  • p(1 or 2 or 3) = 1/6 + 1/6 + 1/6 = 0.5

Manipulating probability

• The sum rule
  • p(1 or 2 or 3) = 1/6 + 1/6 + 1/6 = 0.5
• The product rule

Manipulating probability

• The sum rule
  • p(1 or 2 or 3) = 1/6 + 1/6 + 1/6 = 0.5
• The product rule
  • p(6 and 6)

Manipulating probability

• The sum rule
  • p(1 or 2 or 3) = 1/6 + 1/6 + 1/6 = 0.5
• The product rule
  • p(6 and 6) = 1/6 * 1/6 = 1 / 36 = 2.8%

Manipulating probability

• The sum rule
  • p(1 or 2 or 3) = 1/6 + 1/6 + 1/6 = 0.5
• The product rule
  • p(6 and 6) = 1/6 * 1/6 = 1 / 36 = 2.8%

 

• Foundations of Probability in R

Let's try out these rules!

Fundamentals of Bayesian Data Analysis in R