Markowitz portfolios

Introduction to Portfolio Risk Management in Python

Dakota Wixom

Quantitative Analyst | QuantCourse.com

100,000 randomly generated portfolios

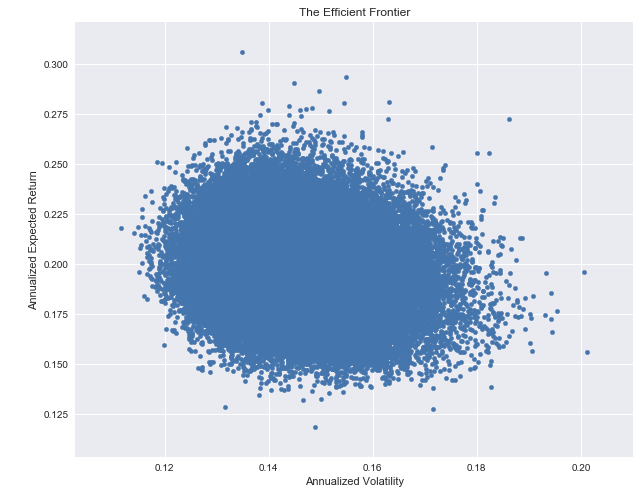
Sharpe ratio

The Sharpe ratio is a measure of risk-adjusted return.

To calculate the 1966 version of the Sharpe ratio:

$$ S = \frac{ R_a - r_f }{\sigma_a} $$

S: Sharpe Ratio
$ R_a $: Asset return
$ r_f $: Risk-free rate of return
$ \sigma_a $: Asset volatility

The efficient frontier

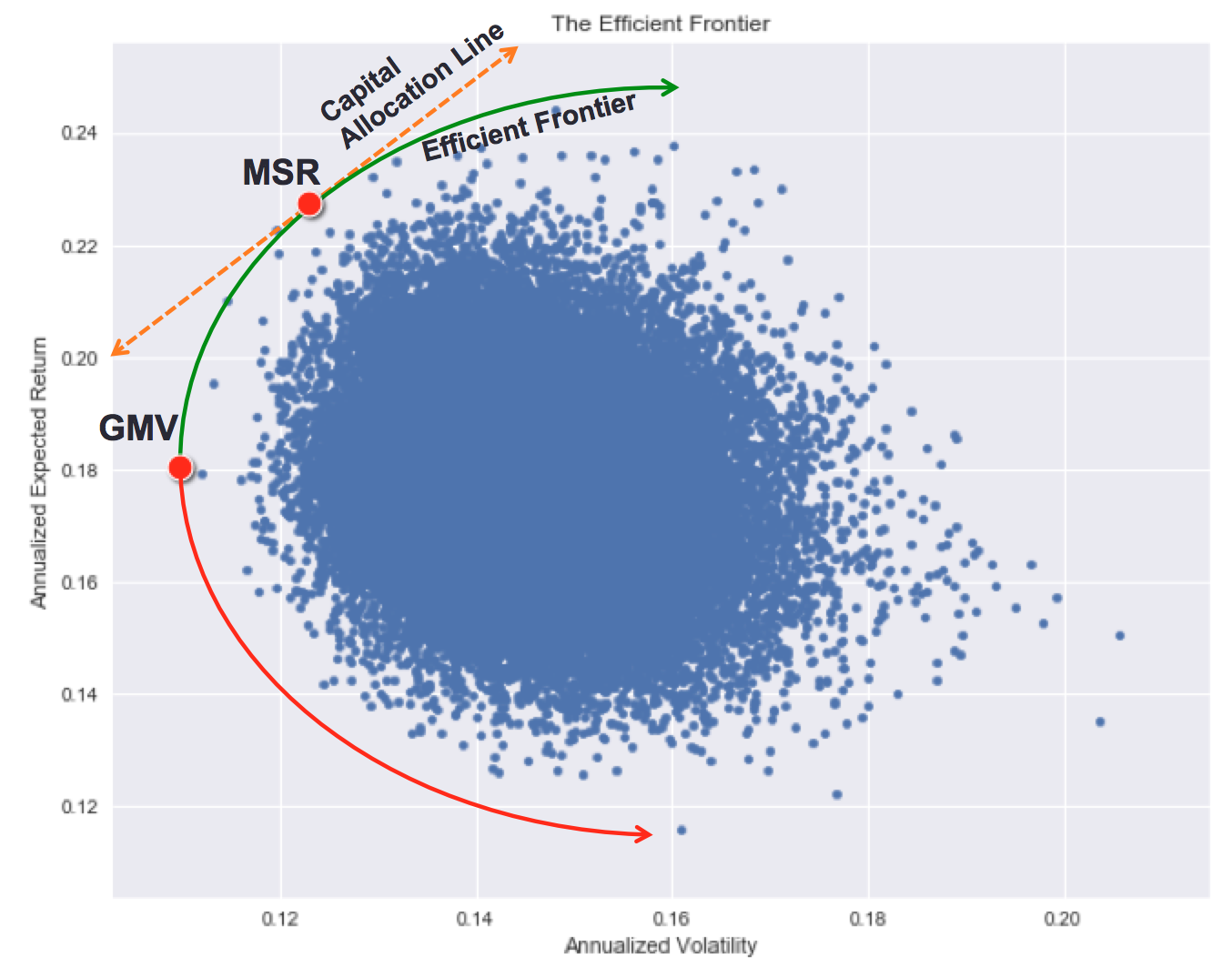
The Markowitz portfolios

Any point on the efficient frontier is an optimum portfolio.

These two common points are called Markowitz Portfolios:

MSR: Max Sharpe Ratio portfolio
GMV: Global Minimum Volatility portfolio

Choosing a portfolio

How do you choose the best portfolio?

Try to pick a portfolio on the bounding edge of the efficient frontier
Higher return is available if you can stomach higher risk

Selecting the MSR in Python

Assuming a DataFrame df of random portfolios with Volatility and Returns columns:

numstocks = 5
risk_free = 0
df["Sharpe"] = (df["Returns"] - risk_free) / df["Volatility"]
MSR = df.sort_values(by=['Sharpe'], ascending=False)
MSR_weights = MSR.iloc[0, 0:numstocks]
np.array(MSR_weights)

array([0.15, 0.35, 0.10, 0.15, 0.25])

Past performance is not a guarantee of future returns

Even though a Max Sharpe Ratio portfolio might sound nice, in practice, returns are extremely difficult to predict.

Selecting the GMV in Python

Assuming a DataFrame df of random portfolios with Volatility and Returns columns:

numstocks = 5
GMV = df.sort_values(by=['Volatility'], ascending=True)
GMV_weights = GMV.iloc[0, 0:numstocks]
np.array(GMV_weights)

array([0.25, 0.15, 0.35, 0.15, 0.10])

Let's practice!

Introduction to Portfolio Risk Management in Python