Mean, variance, and normal distribution

Introduction to Portfolio Risk Management in Python

Dakota Wixom

Quantitative Analyst | QuantCourse.com

Moments of distributions

Probability distributions have the following moments:

1) Mean ($ \mu $)
2) Variance ( $ \sigma ^ 2 $ )
3) Skewness
4) Kurtosis

There are many types of distributions. Some are normal and some are non-normal. A random variable with a Gaussian distribution is said to be normally distributed.

Normal Distributions have the following properties:

Mean = $ \mu $
Variance = $ \sigma ^ 2 $
Skewness = 0
Kurtosis = 3

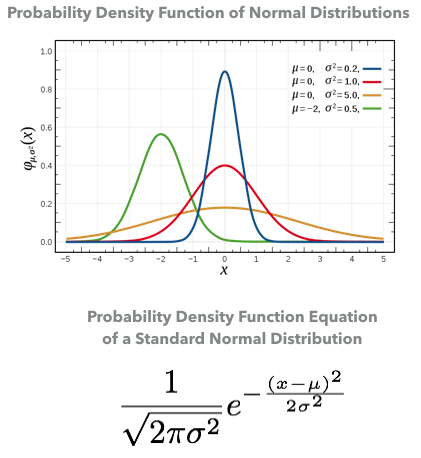
The standard normal distribution

The Standard Normal is a special case of the Normal Distribution when:

$ \sigma $ = 1
$ \mu $ = 0

Comparing against a normal distribution

Normal distributions have a skewness near 0 and a kurtosis near 3.
Financial returns tend not to be normally distributed
Financial returns can have high kurtosis

Comparing against a normal distribution

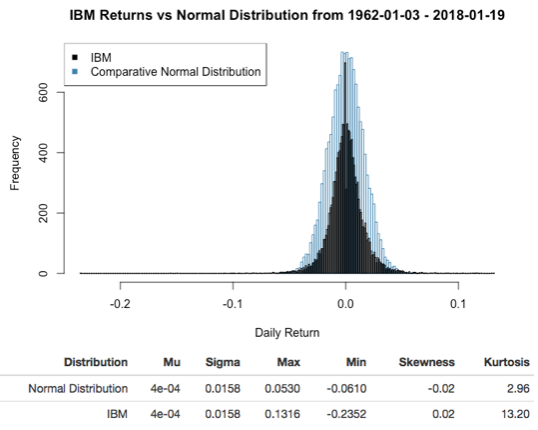
Calculating mean returns in python

To calculate the average daily return, use the np.mean() function:

import numpy as np
np.mean(StockPrices["Returns"])

0.0003

To calculate the average annualized return assuming 252 trading days in a year:

import numpy as np
((1+np.mean(StockPrices["Returns"]))**252)-1

0.0785

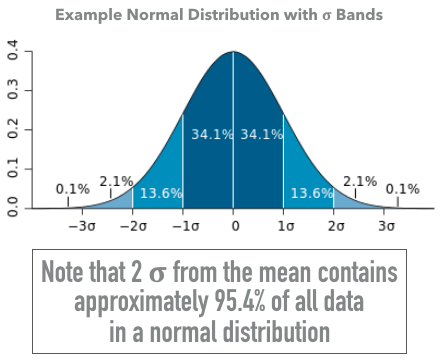
Standard deviation and variance

Standard Deviation (Volatility)

Variance = $ \sigma ^ 2 $
Often represented in mathematical notation as $ \sigma $, or referred to as volatility
An investment with higher $ \sigma $ is viewed as a higher risk investment
Measures the dispersion of returns

Standard deviation and variance in Python

Assume you have pre-loaded stock returns data in the StockData object. To calculate the periodic standard deviation of returns:

import numpy as np
np.std(StockPrices["Returns"])

0.0256

To calculate variance, simply square the standard deviation:

np.std(StockPrices["Returns"])**2

0.000655

Scaling volatility

Volatility scales with the square root of time
You can normally assume 252 trading days in a given year, and 21 trading days in a given month

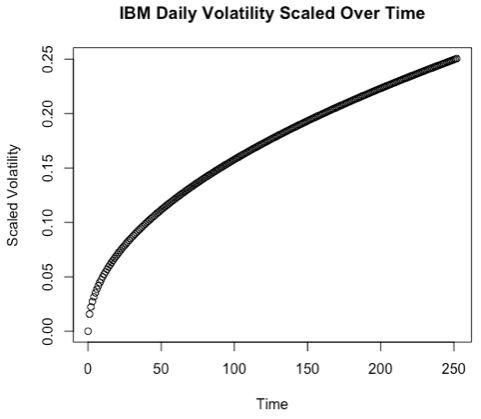
Scaling volatility in Python

Assume you have pre-loaded stock returns data in the StockData object. To calculate the annualized volatility of returns:

import numpy as np
np.std(StockPrices["Returns"]) * np.sqrt(252)

0.3071

Let's practice!

Introduction to Portfolio Risk Management in Python