The Capital Asset Pricing Model

Introduction to Portfolio Risk Management in Python

Dakota Wixom

Quantitative Analyst | QuantCourse.com

The founding father of asset pricing models

CAPM

The Capital Asset Pricing Model is the fundamental building block for many other asset pricing models and factor models in finance.

Introduction to Portfolio Risk Management in Python

Excess returns

To calculate excess returns, simply subtract the risk free rate of return from your total return:

$$ \text{Excess Return} = \text{Return} - \text{Risk Free Return} $$

Example:

Investing in Brazil:

10% Portfolio Return - 15% Risk Free Rate = -5% Excess Return

Investing in the US:

10% Portfolio Return - 3% Risk Free Rate = 7% Excess Return

Introduction to Portfolio Risk Management in Python

The Capital Asset Pricing Model

$$ E(R_{P}) - RF = \beta_{{P}}(E(R_{M})-RF)\ $$

  • $E(R_{P}) - RF$: The excess expected return of a stock or portfolio P
  • $E(R_{M}) - RF$: The excess expected return of the broad market portfolio B
  • $RF$: The regional risk free-rate
  • $\beta_{{P}}$: Portfolio beta, or exposure, to the broad market portfolio B
Introduction to Portfolio Risk Management in Python

Calculating Beta using co-variance

To calculate historical beta using co-variance:

$$ \beta_P = \frac{Cov(R_P, R_B)}{Var(R_B)} $$

  • $\beta_P$: Portfolio beta
  • $Cov(R_P, R_B)$: The co-variance between the portfolio (P) and the benchmark market index (B)
  • $Var(R_B)$: The variance of the benchmark market index
Introduction to Portfolio Risk Management in Python

Calculating Beta using co-variance in Python

Assuming you already have excess portfolio and market returns in the object Data:

covariance_matrix = Data[["Port_Excess","Mkt_Excess"]].cov()
covariance_coefficient = covariance_matrix.iloc[0, 1]
benchmark_variance = Data["Mkt_Excess"].var()
portfolio_beta = covariance_coefficient / benchmark_variance
portfolio_beta

0.93
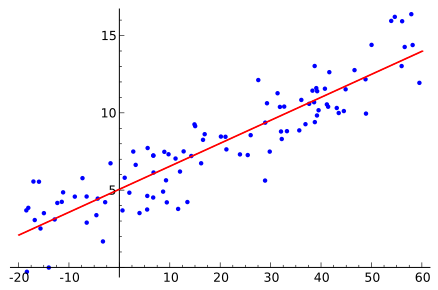
Introduction to Portfolio Risk Management in Python

Linear regressions

Example of a linear regression:

Regression formula in matrix notation:

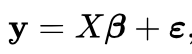
Introduction to Portfolio Risk Management in Python

Calculating Beta using linear regression

Assuming you already have excess portfolio and market returns in the object Data:

import statsmodels.formula.api as smf
model = smf.ols(formula='Port_Excess ~ Mkt_Excess', data=Data)
fit = model.fit()
beta = fit.params["Mkt_Excess"]
beta

0.93
Introduction to Portfolio Risk Management in Python

R-Squared vs Adjusted R-Squared

To extract the adjusted r-squared and r-squared values:

import statsmodels.formula.api as smf
model = smf.ols(formula='Port_Excess ~ Mkt_Excess', data=Data)
fit = model.fit()
r_squared = fit.rsquared
r_squared

0.70

adjusted_r_squared = fit.rsquared_adj

0.65
Introduction to Portfolio Risk Management in Python

Let's practice!

Introduction to Portfolio Risk Management in Python

Preparing Video For Download...