Correlation and co-variance

Introduction to Portfolio Risk Management in Python

Dakota Wixom

Quantitative Analyst | QuantCourse.com

Pearson correlation

Examples of different correlations between two random variables:

Introduction to Portfolio Risk Management in Python

Pearson correlation

A heatmap of a correlation matrix:

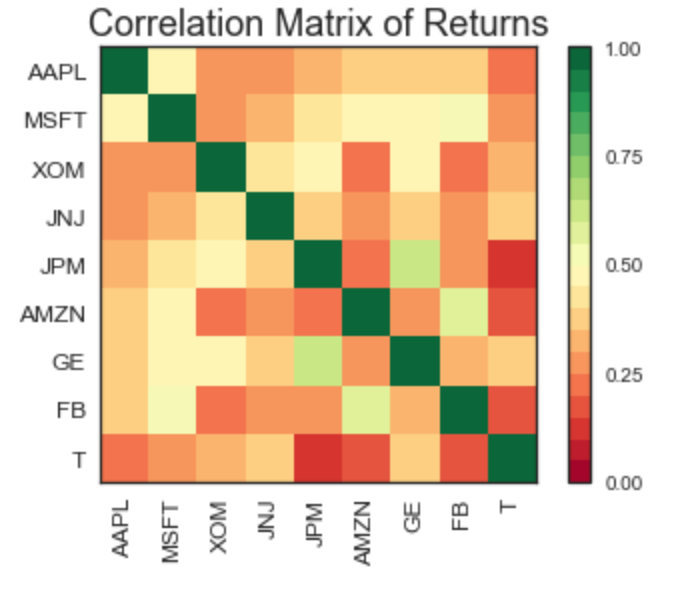
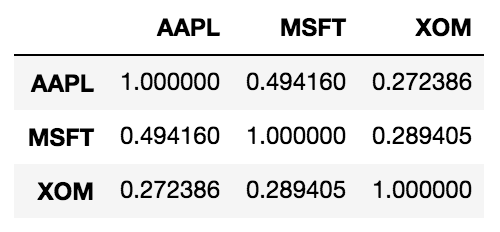
Introduction to Portfolio Risk Management in Python

Correlation matrix in Python

Assuming StockReturns is a pandas DataFrame of stock returns, you can calculate the correlation matrix as follows:

correlation_matrix = StockReturns.corr()
print(correlation_matrix)

Introduction to Portfolio Risk Management in Python

Portfolio standard deviation

Portfolio standard deviation for a two asset portfolio:

$$ \sigma_p = \sqrt{ w_1^2 \sigma_1^2 + w_2^2 \sigma_2^2 + 2 w_1 w_2 \rho_{1, 2} \sigma_1 \sigma_2 }$$

  • $\sigma_p$: Portfolio standard deviation
  • w: Asset weight
  • $\sigma$: Asset volatility
  • $\rho_{1, 2}$: Correlation between assets 1 and 2
Introduction to Portfolio Risk Management in Python

The Co-variance matrix

To calculate the co-variance matrix ($ \Sigma $) of returns X:

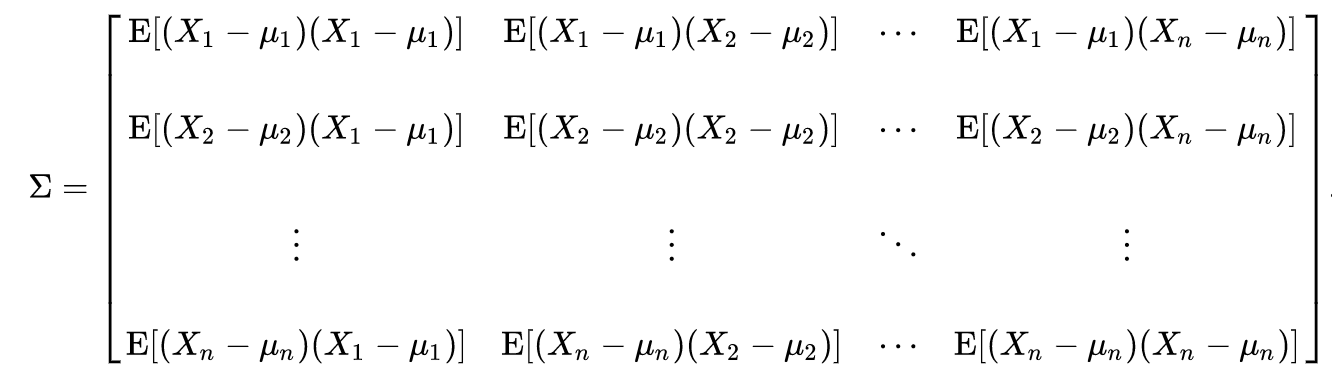
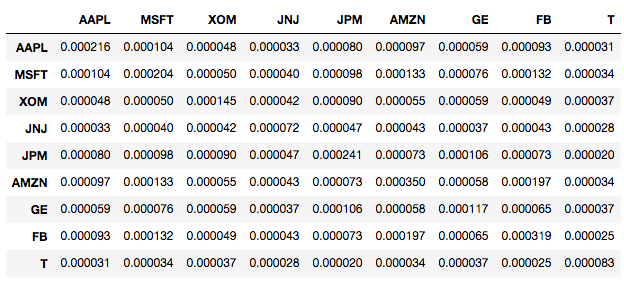
Introduction to Portfolio Risk Management in Python

The Co-variance matrix in Python

Assuming StockReturns is a pandas DataFrame of stock returns, you can calculate the covariance matrix as follows:

cov_mat = StockReturns.cov()
cov_mat

Introduction to Portfolio Risk Management in Python

Annualizing the covariance matrix

To annualize the covariance matrix:

cov_mat_annual = cov_mat * 252
Introduction to Portfolio Risk Management in Python

Portfolio standard deviation using covariance

The formula for portfolio volatility is:

$$ \sigma_{Portfolio} = \sqrt{ w_T \cdot \Sigma \cdot w } $$

  • $ \sigma_{Portfolio} $: Portfolio volatility
  • $ \Sigma $: Covariance matrix of returns
  • w: Portfolio weights ($ w_T $ is transposed portfolio weights)
  • $ \cdot $ The dot-multiplication operator
Introduction to Portfolio Risk Management in Python

Matrix transpose

Examples of matrix transpose operations:

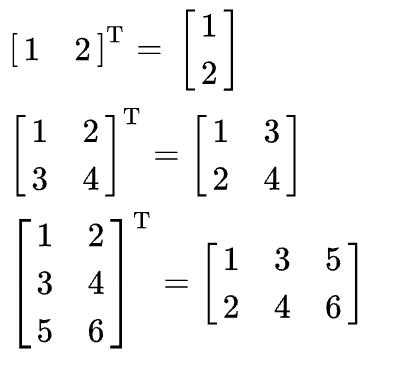
Introduction to Portfolio Risk Management in Python

Dot product

The dot product operation of two vectors a and b:

Introduction to Portfolio Risk Management in Python

Portfolio standard deviation using Python

To calculate portfolio volatility assume a weights array and a covariance matrix:

import numpy as np
port_vol = np.sqrt(np.dot(weights.T, np.dot(cov_mat, weights)))
port_vol

0.035
Introduction to Portfolio Risk Management in Python

Let's practice!

Introduction to Portfolio Risk Management in Python

Preparing Video For Download...