Interpreting a Confidence Interval

Inference for Categorical Data in R

Andrew Bray

Assistant Professor of Statistics at Reed College

Confidence intervals

Conclusion: the true proportion of Americans that are happy is between 0.705 and 0.841.

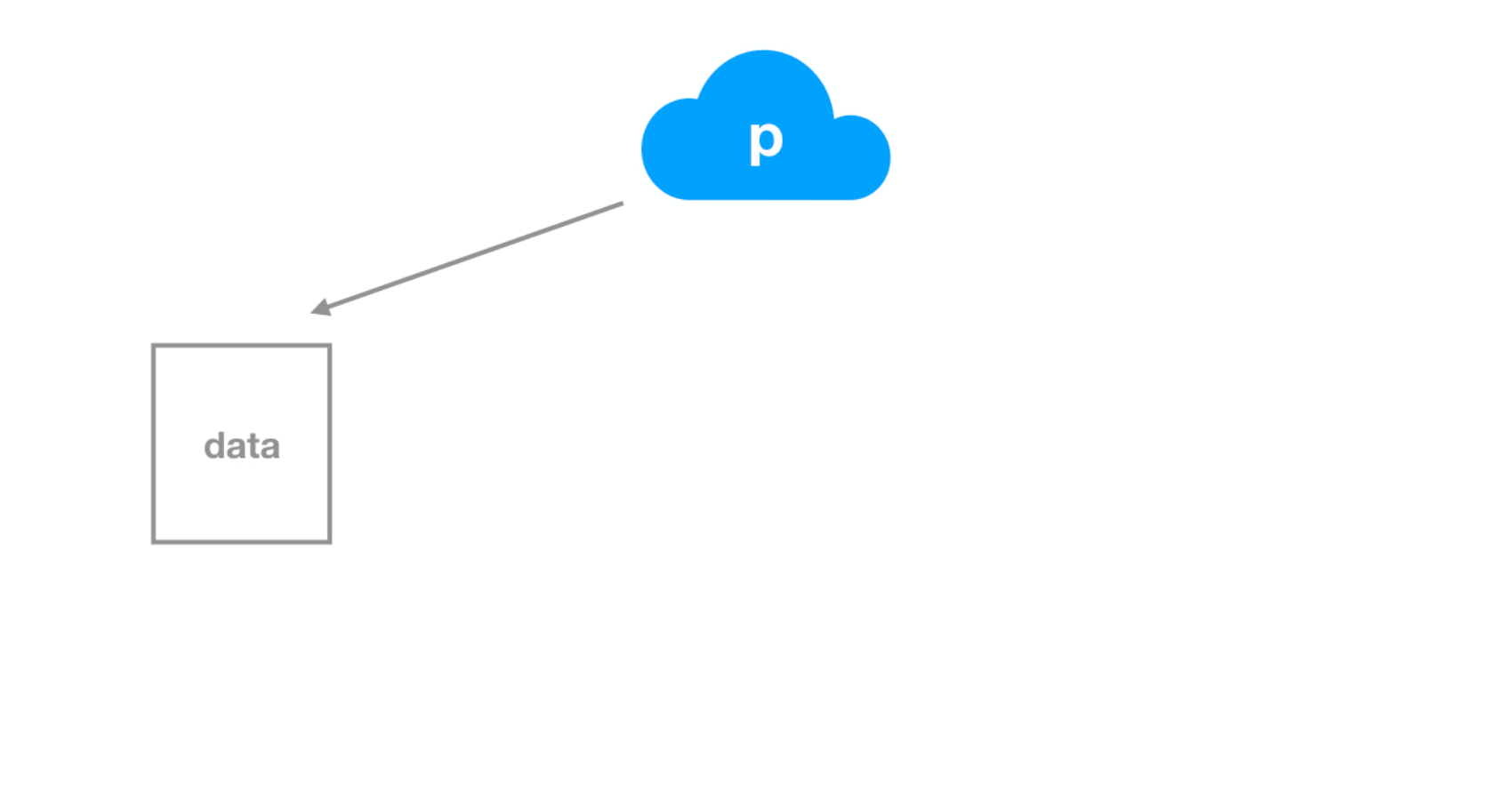
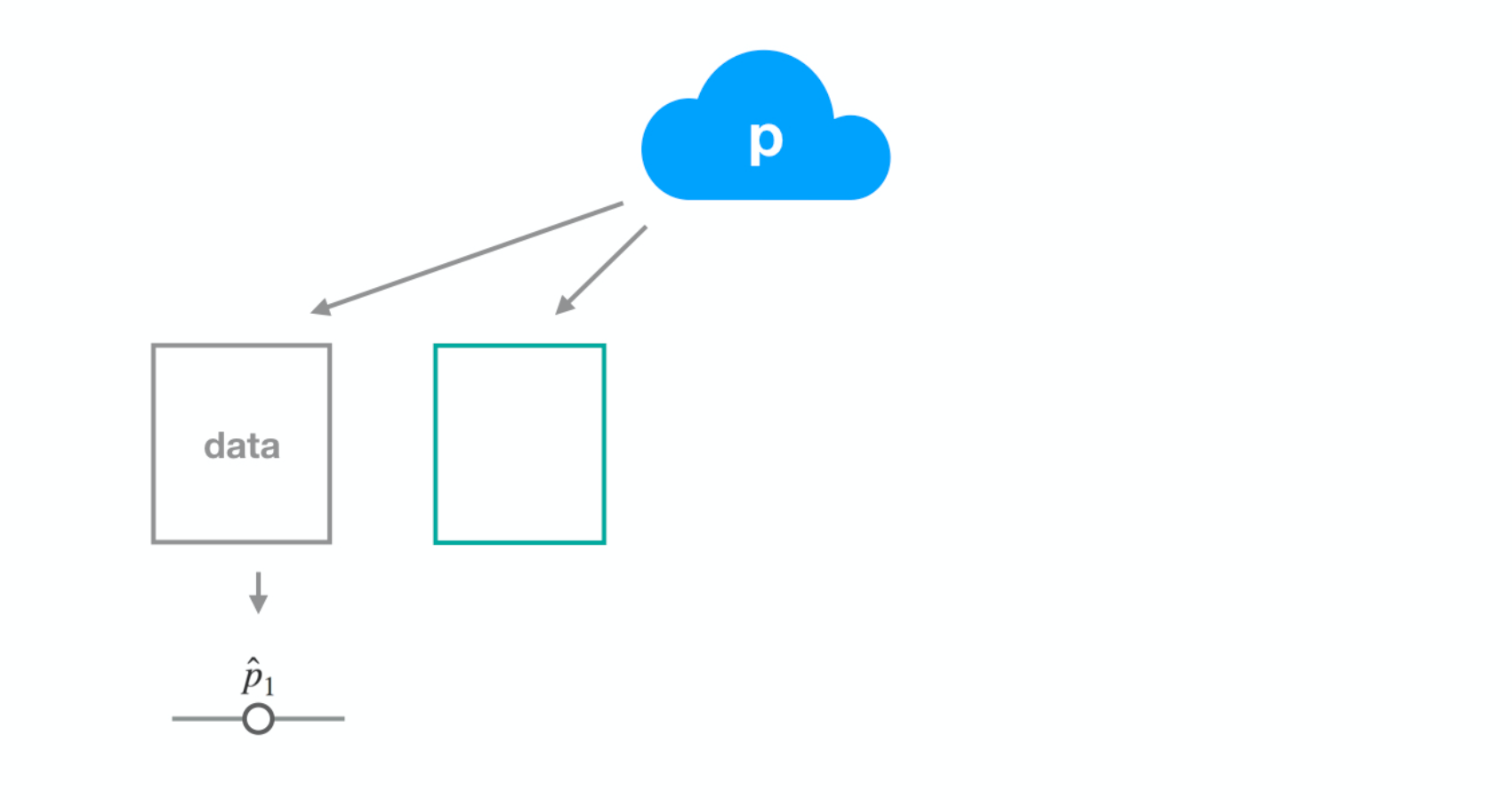
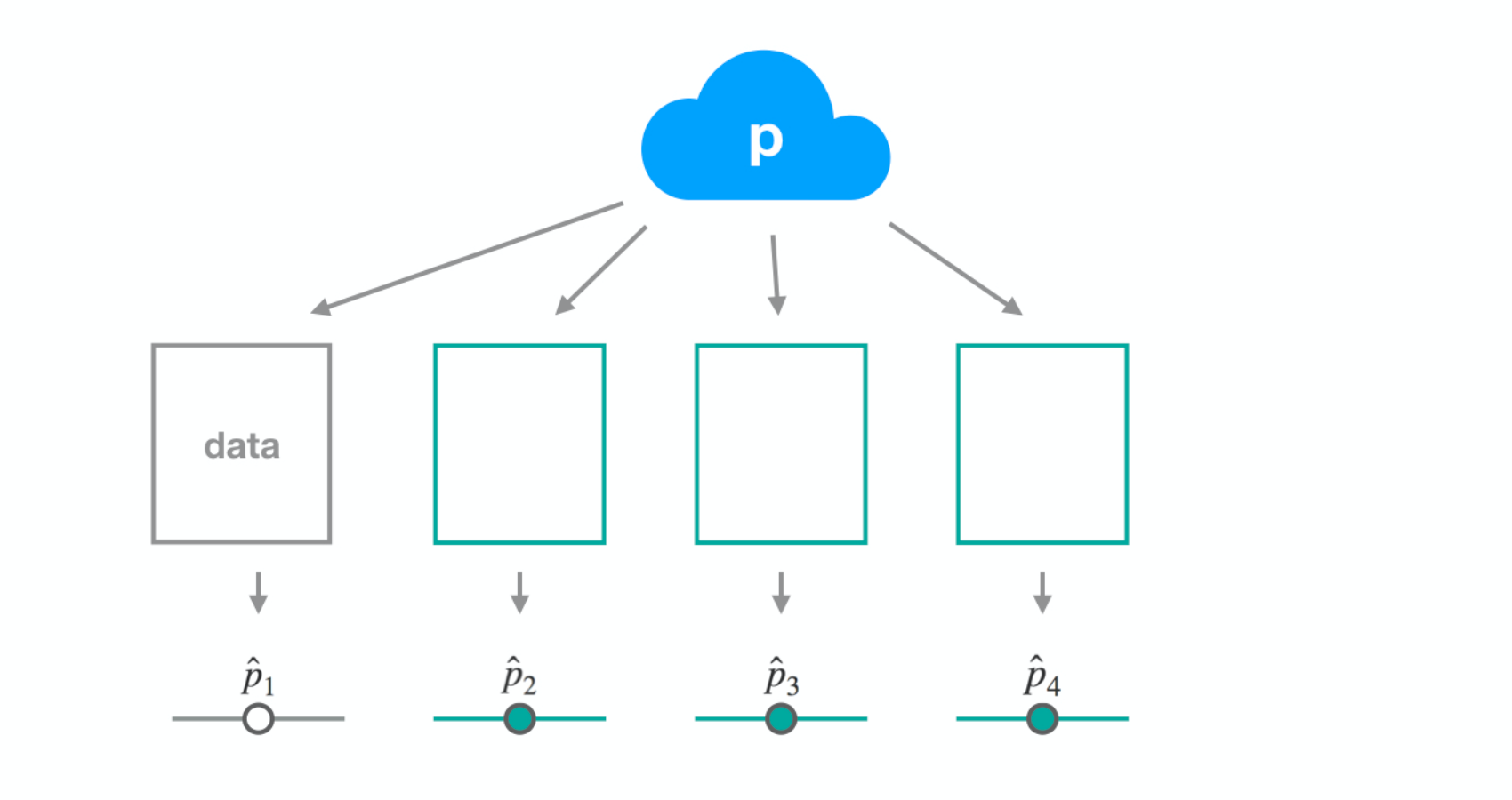
What do we mean by confident?

Inference for Categorical Data in R

Dataset 1

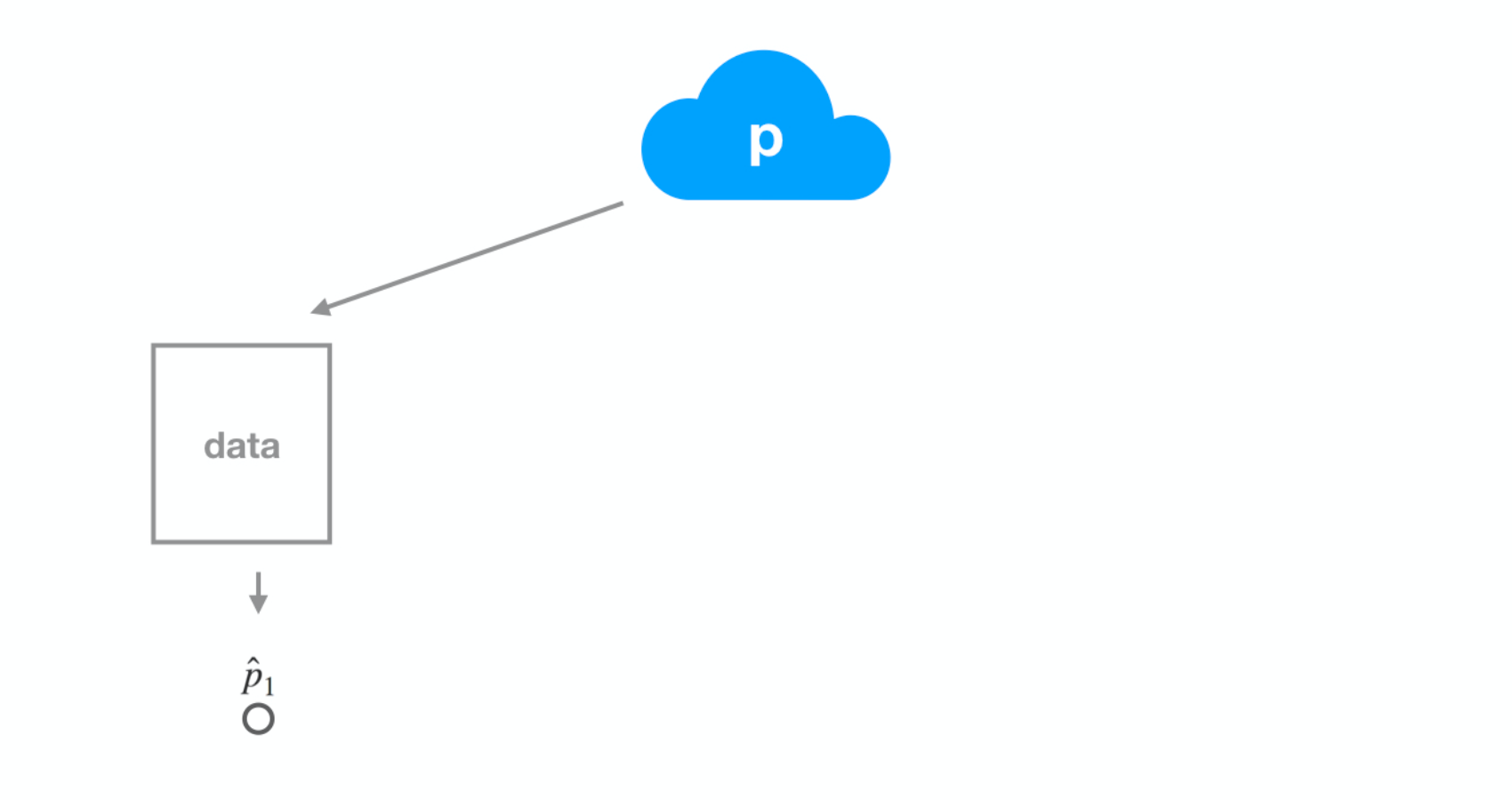
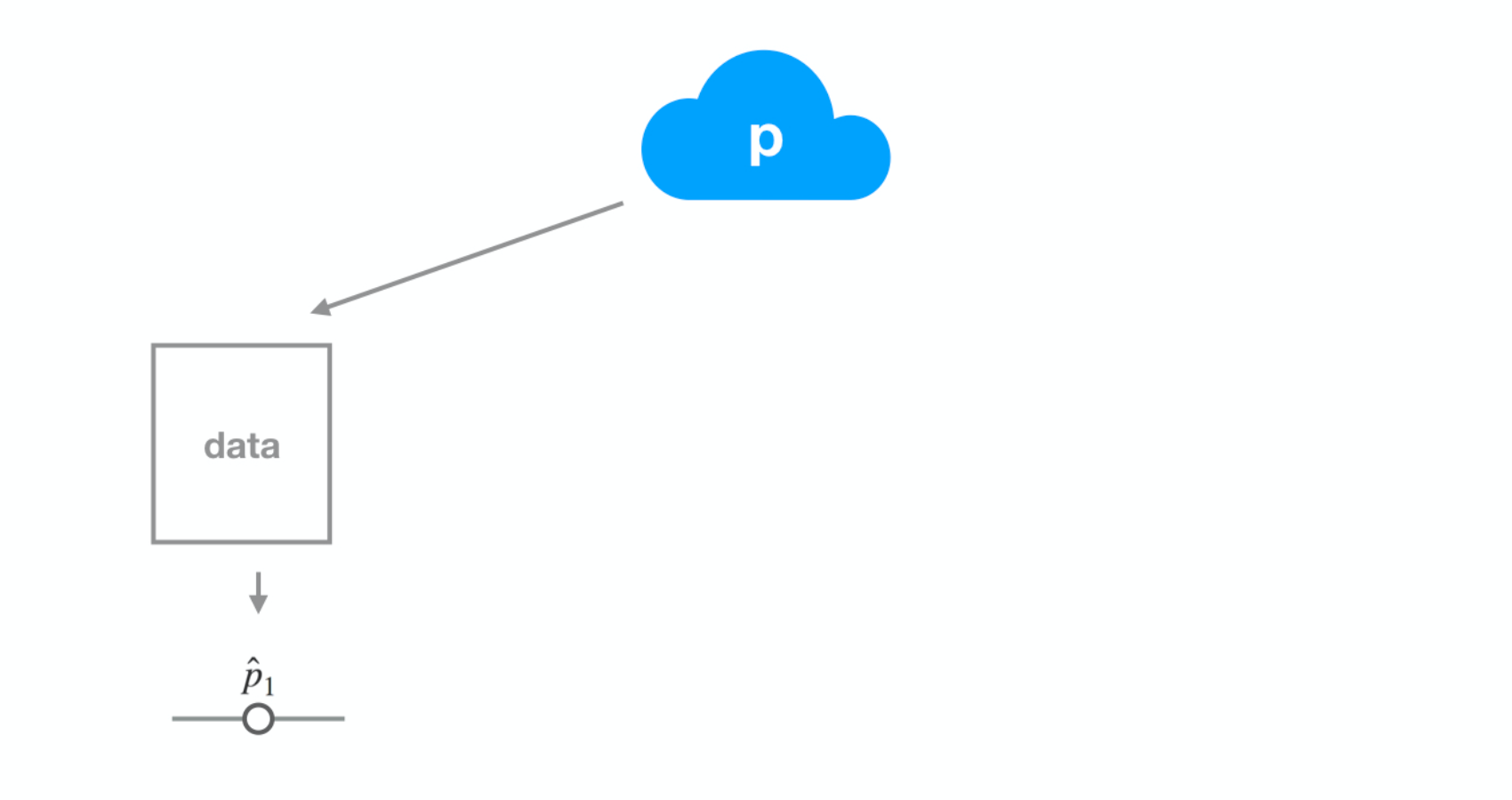
ds1 <- filter(gss, year == 2016)

p_hat <- ds1 %>%
  summarize(mean(happy == "HAPPY")) %>% 
  pull()

SE <- ds1 %>%
  specify(response = happy, 
          success = "HAPPY") %>%
  generate(reps = 500, 
           type = "bootstrap") %>%
  calculate(stat = "prop") %>%
  summarize(sd(stat)) %>% 
  pull()

c(p_hat - 2 * SE, p_hat + 2 * SE)

0.7073114 0.8393553

confidence-interval

Inference for Categorical Data in R

one.png

Inference for Categorical Data in R

two.png

Inference for Categorical Data in R

three.png

Inference for Categorical Data in R

four.png

Inference for Categorical Data in R

five.png

Inference for Categorical Data in R

six.png

Inference for Categorical Data in R

seven.png

Inference for Categorical Data in R

eight.png

Inference for Categorical Data in R

nine.png

Inference for Categorical Data in R

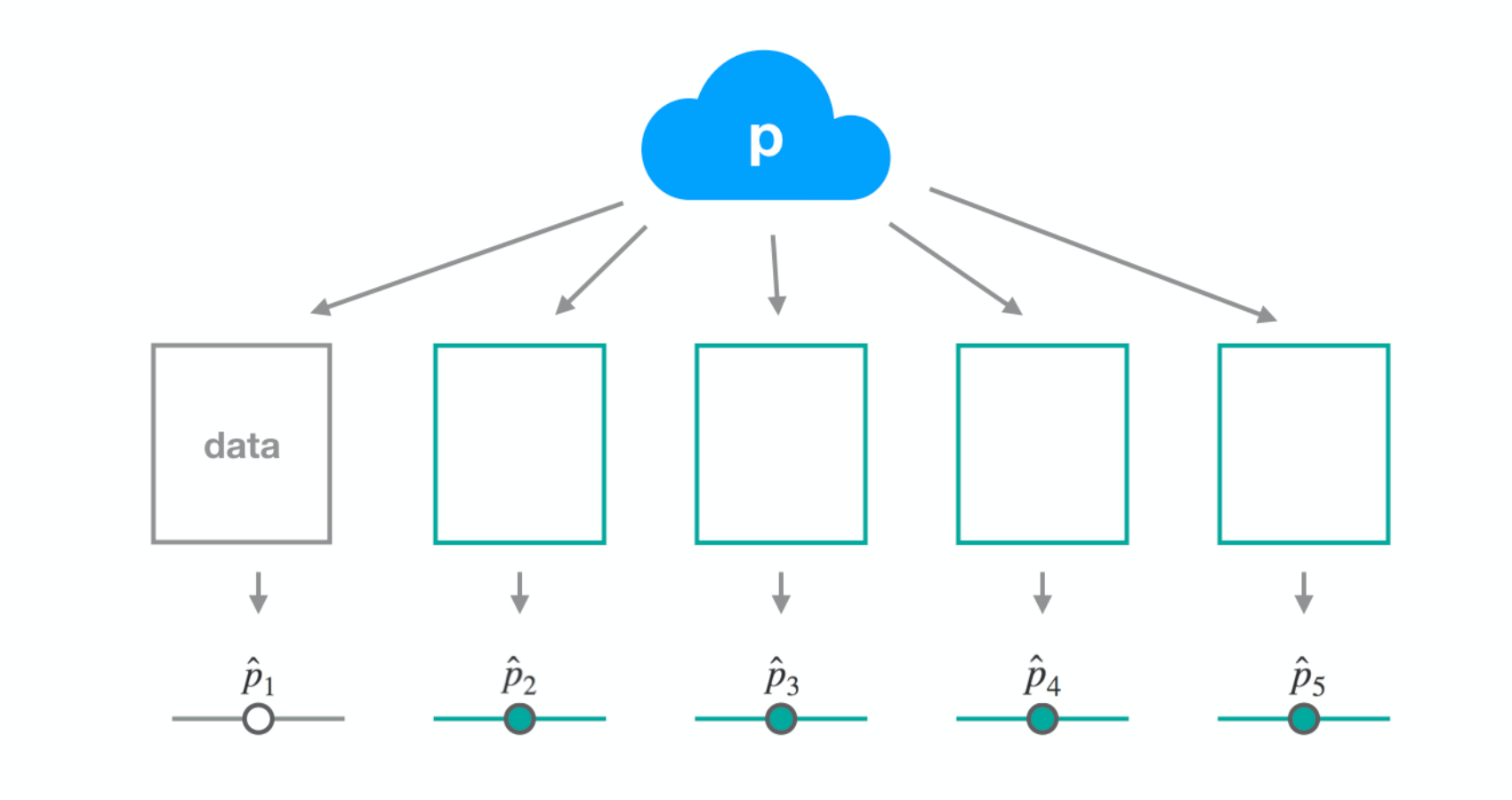
ten.png

Inference for Categorical Data in R

Dataset 2

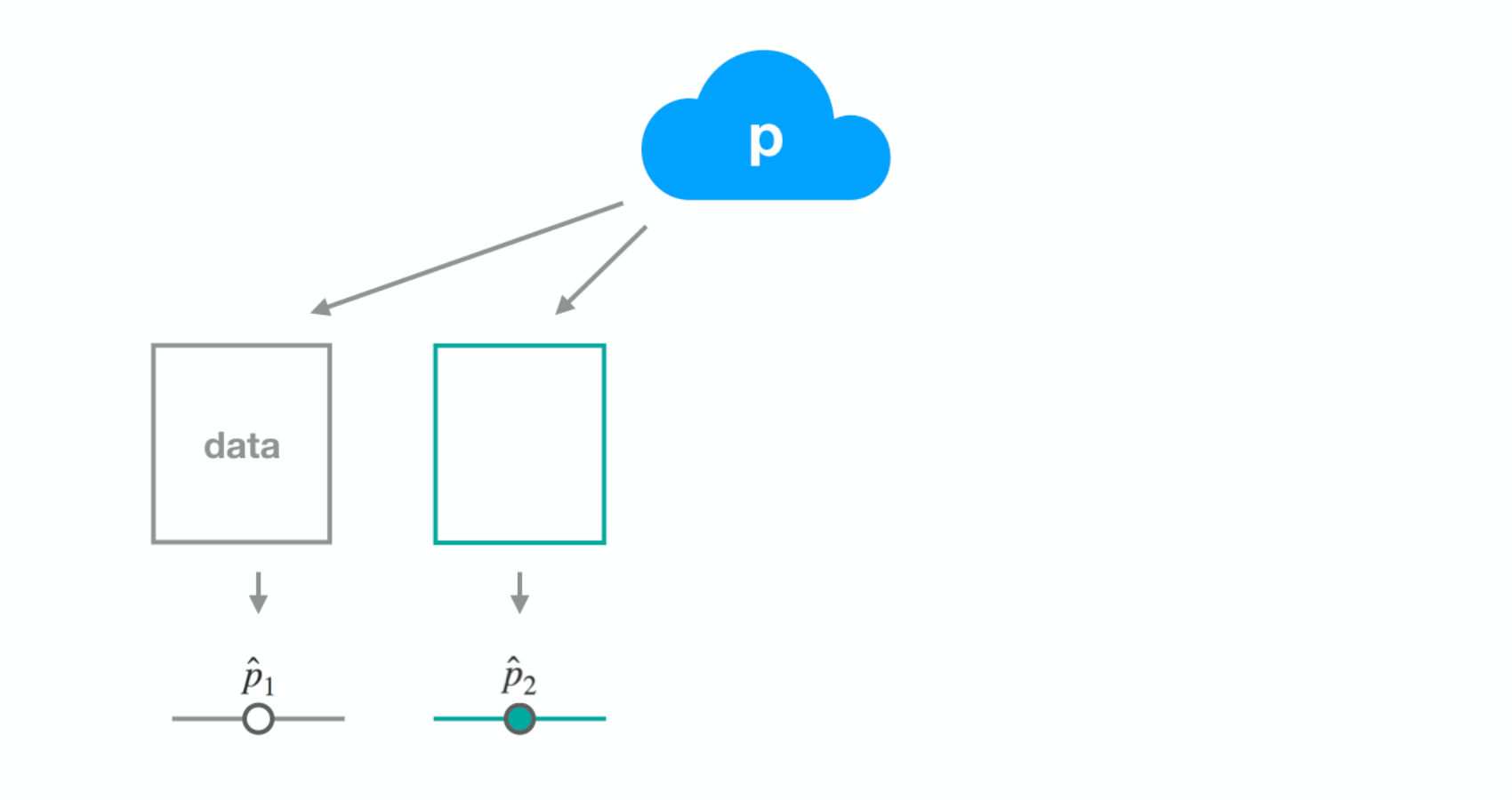
ds2 <- filter(gss, year == 2014)

p_hat <- ds1 %>%
  summarize(mean(happy == "HAPPY")) %>% 
  pull()

SE <- ds1 %>%
  specify(response = happy, 
          success = "HAPPY") %>%
  generate(reps = 500, 
           type = "bootstrap") %>%
  calculate(stat = "prop") %>%
  summarize(sd(stat)) %>% 
  pull()

c(p_hat - 2 * SE, p_hat + 2 * SE)

0.8348831 0.9384503

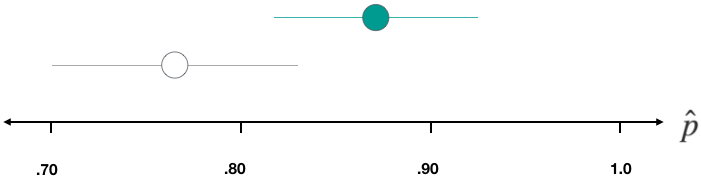
Screenshot 2019-02-21 18.05.03.png

Inference for Categorical Data in R

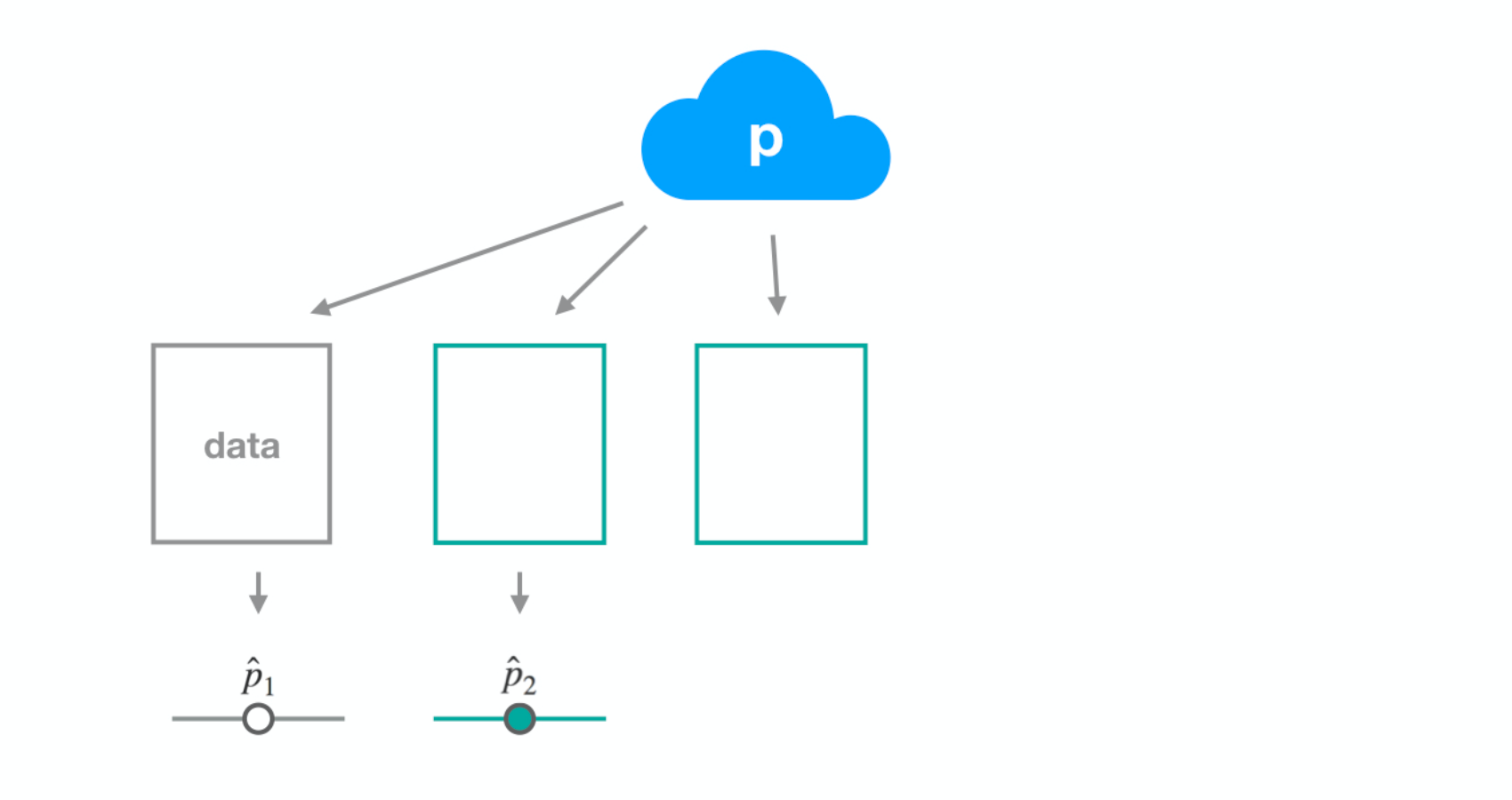
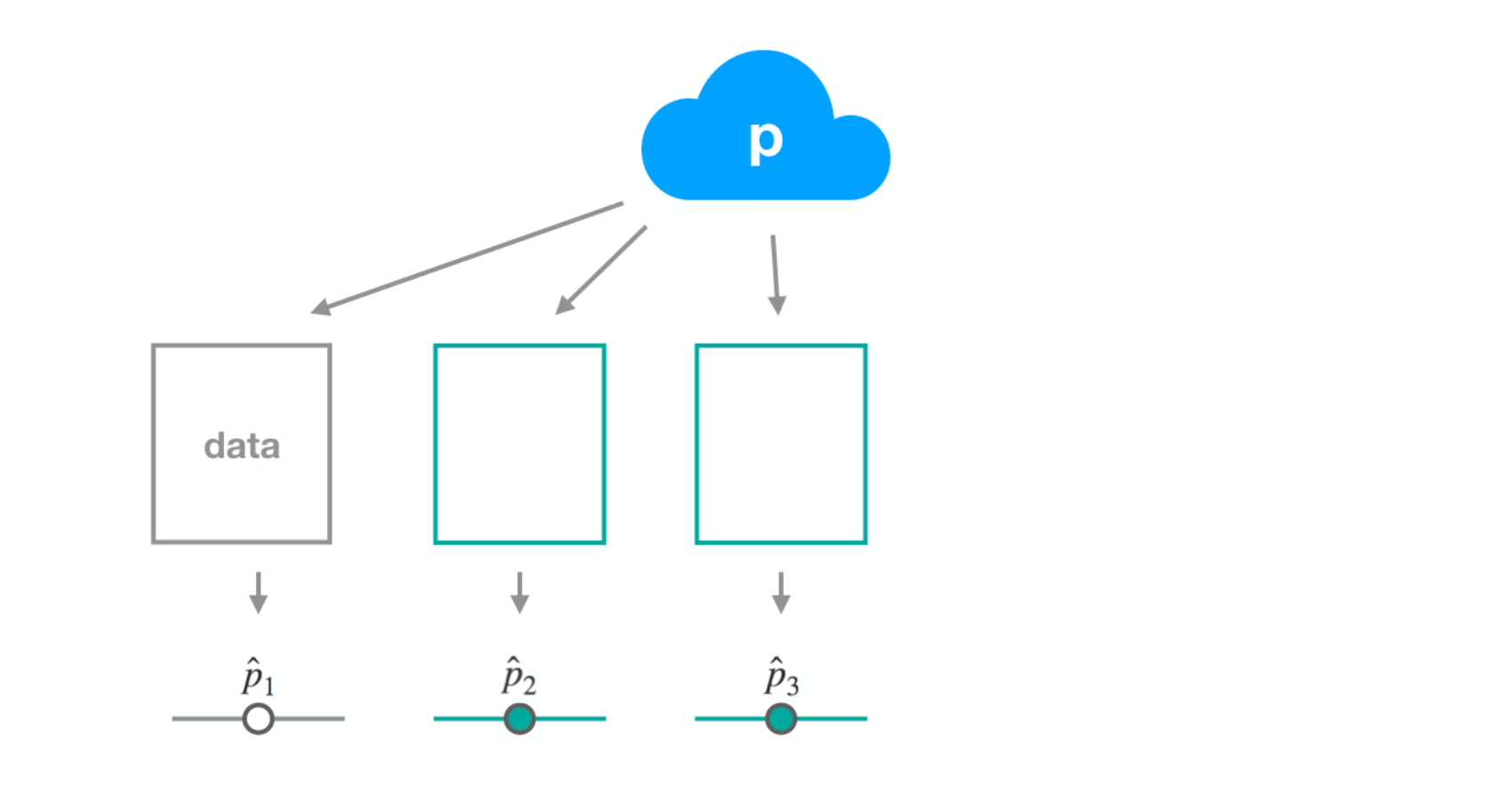
Dataset 3

ds3 <- filter(gss, year == 2012)

p_hat <- ds1 %>%
  summarize(mean(happy == "HAPPY")) %>% 
  pull()

SE <- ds1 %>%
  specify(response = happy, 
          success = "HAPPY") %>%
  generate(reps = 500, 
           type = "bootstrap") %>%
  calculate(stat = "prop") %>%
  summarize(sd(stat)) %>% 
  pull()

c(p_hat - 2 * SE, p_hat + 2 * SE)

0.7626359 0.8906974

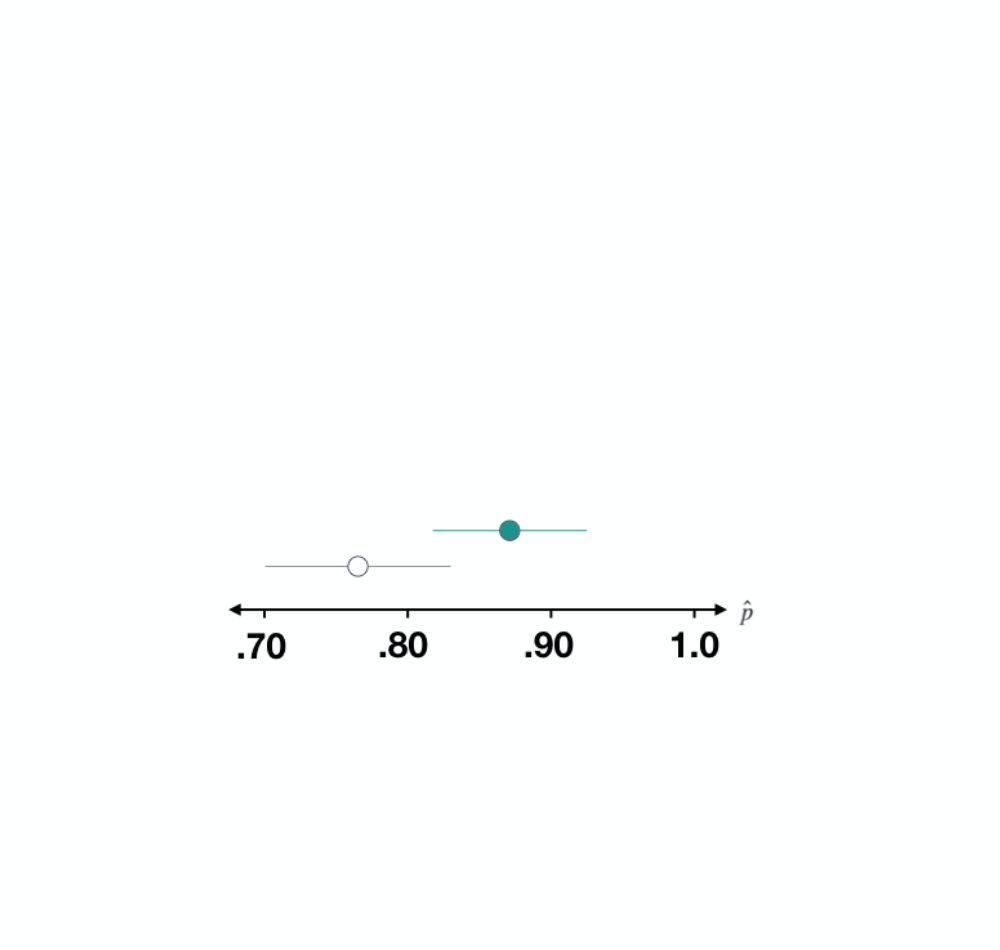
1-2-1.png

Inference for Categorical Data in R

Dataset 3

ds3 <- filter(gss, year == 2012)
p_hat <- ds3 %>%
  summarize(mean(happy == "HAPPY")) %>%
  pull()
SE <- ds3 %>%
  specify(response = happy, 
          success = "HAPPY") %>%
  generate(reps = 500, 
           type = "bootstrap") %>%
  calculate(stat = "prop") %>%
  summarize(sd(stat)) %>%
  pull()

c(p_hat - 2 * SE, p_hat + 2 * SE)

0.7626359 0.8906974

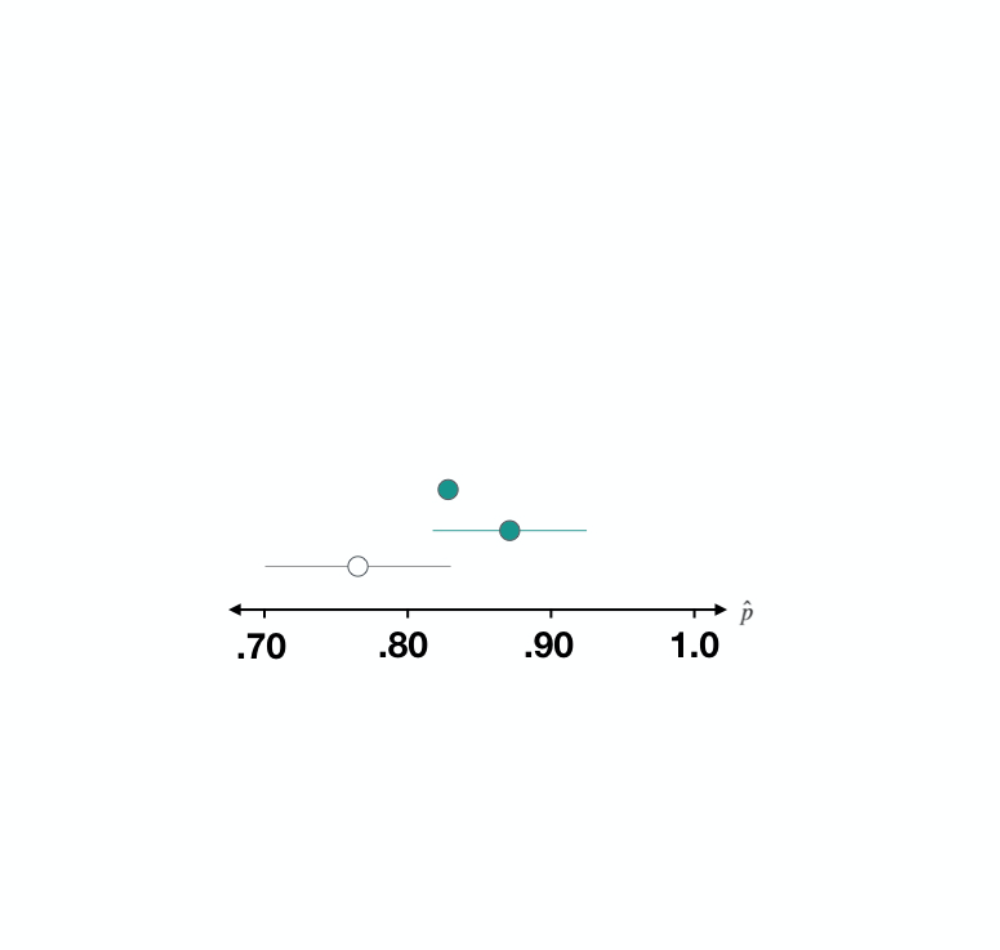
1-2-2.png

Inference for Categorical Data in R

Dataset 3

ds3 <- filter(gss, year == 2012)
p_hat <- ds3 %>%
  summarize(mean(happy == "HAPPY")) %>%
  pull()
SE <- ds3 %>%
  specify(response = happy, 
          success = "HAPPY") %>%
  generate(reps = 500, 
           type = "bootstrap") %>%
  calculate(stat = "prop") %>%
  summarize(sd(stat)) %>%
  pull()

c(p_hat - 2 * SE, p_hat + 2 * SE)

0.7626359 0.8906974

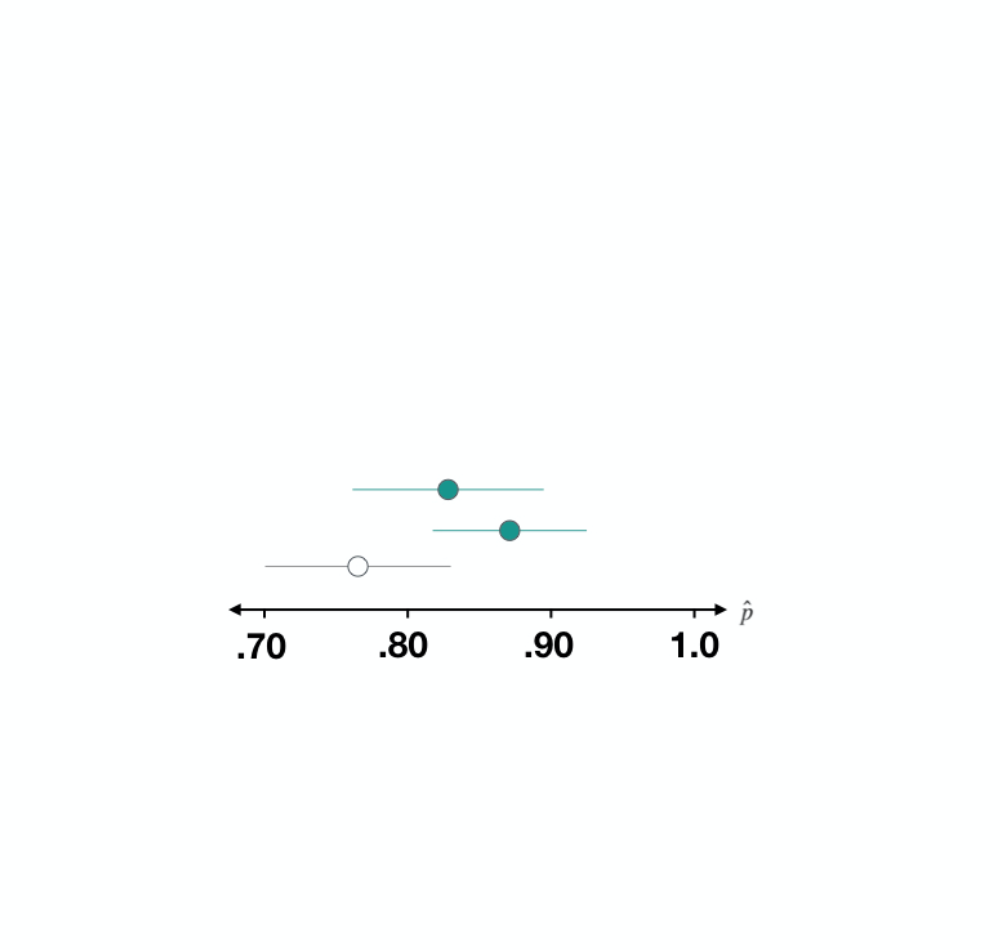
1-2-3.png

Inference for Categorical Data in R

Dataset 3

ds3 <- filter(gss, year == 2012)
p_hat <- ds3 %>%
  summarize(mean(happy == "HAPPY")) %>%
  pull()
SE <- ds3 %>%
  specify(response = happy, 
          success = "HAPPY") %>%
  generate(reps = 500, 
           type = "bootstrap") %>%
  calculate(stat = "prop") %>%
  summarize(sd(stat)) %>%
  pull()

c(p_hat - 2 * SE, p_hat + 2 * SE)

0.7626359 0.8906974

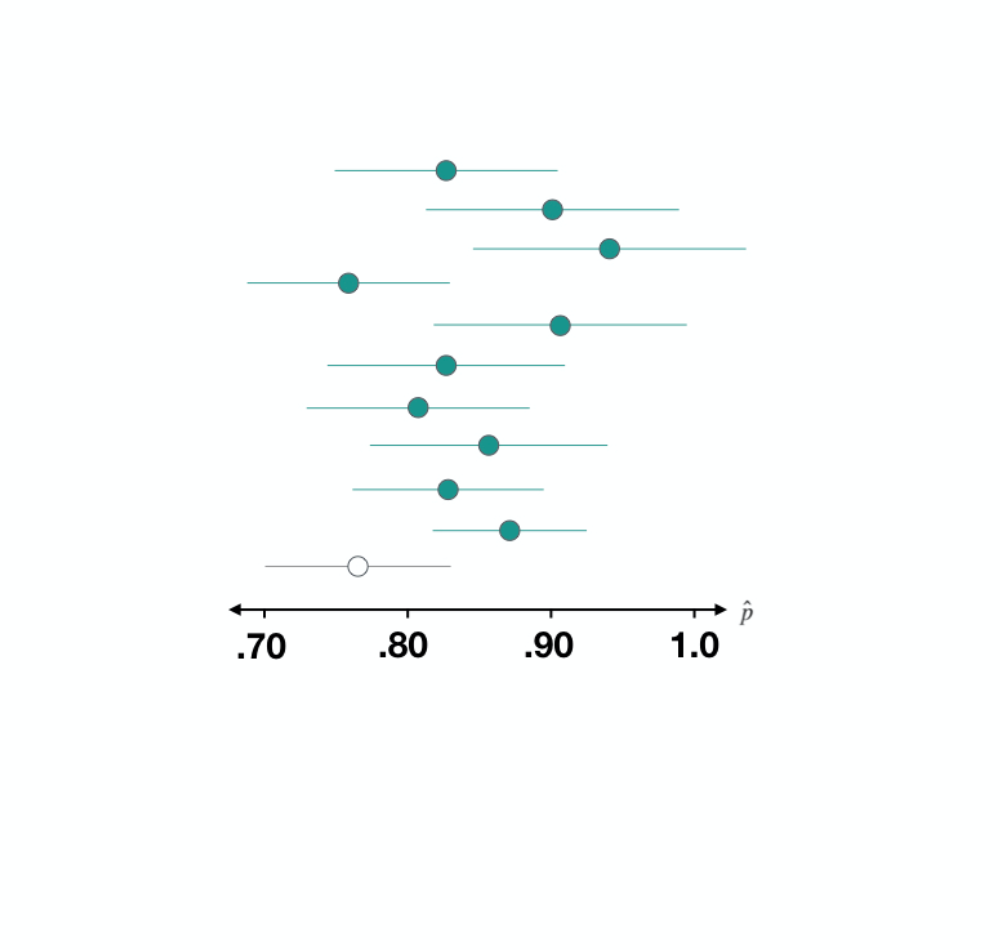
1-2-4.png

Inference for Categorical Data in R

Dataset 3

ds3 <- filter(gss, year == 2012)
p_hat <- ds3 %>%
  summarize(mean(happy == "HAPPY")) %>%
  pull()
SE <- ds3 %>%
  specify(response = happy, 
          success = "HAPPY") %>%
  generate(reps = 500, 
           type = "bootstrap") %>%
  calculate(stat = "prop") %>%
  summarize(sd(stat)) %>%
  pull()

c(p_hat - 2 * SE, p_hat + 2 * SE)

0.7626359 0.8906974

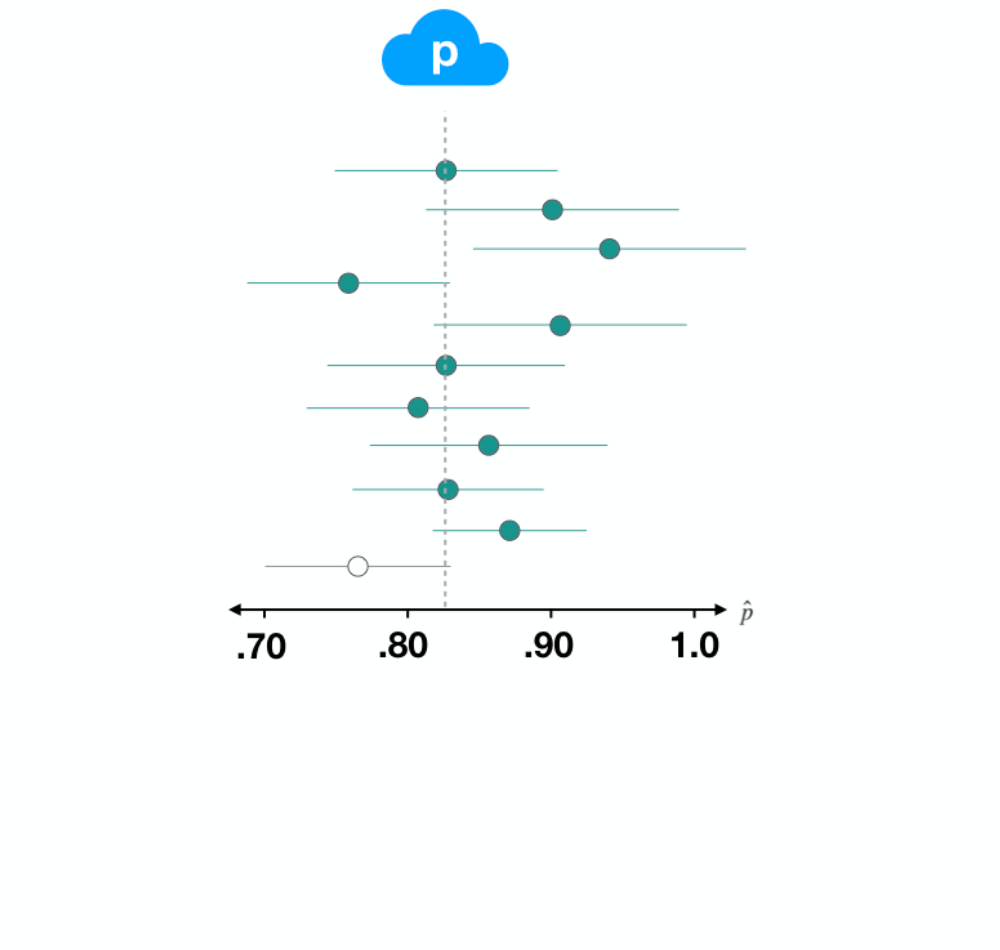
1-2-5.png

Inference for Categorical Data in R

Dataset 3

ds3 <- filter(gss, year == 2012)
p_hat <- ds3 %>%
  summarize(mean(happy == "HAPPY")) %>%
  pull()
SE <- ds3 %>%
  specify(response = happy, 
          success = "HAPPY") %>%
  generate(reps = 500, 
           type = "bootstrap") %>%
  calculate(stat = "prop") %>%
  summarize(sd(stat)) %>%
  pull()

c(p_hat - 2 * SE, p_hat + 2 * SE)

0.7626359 0.8906974

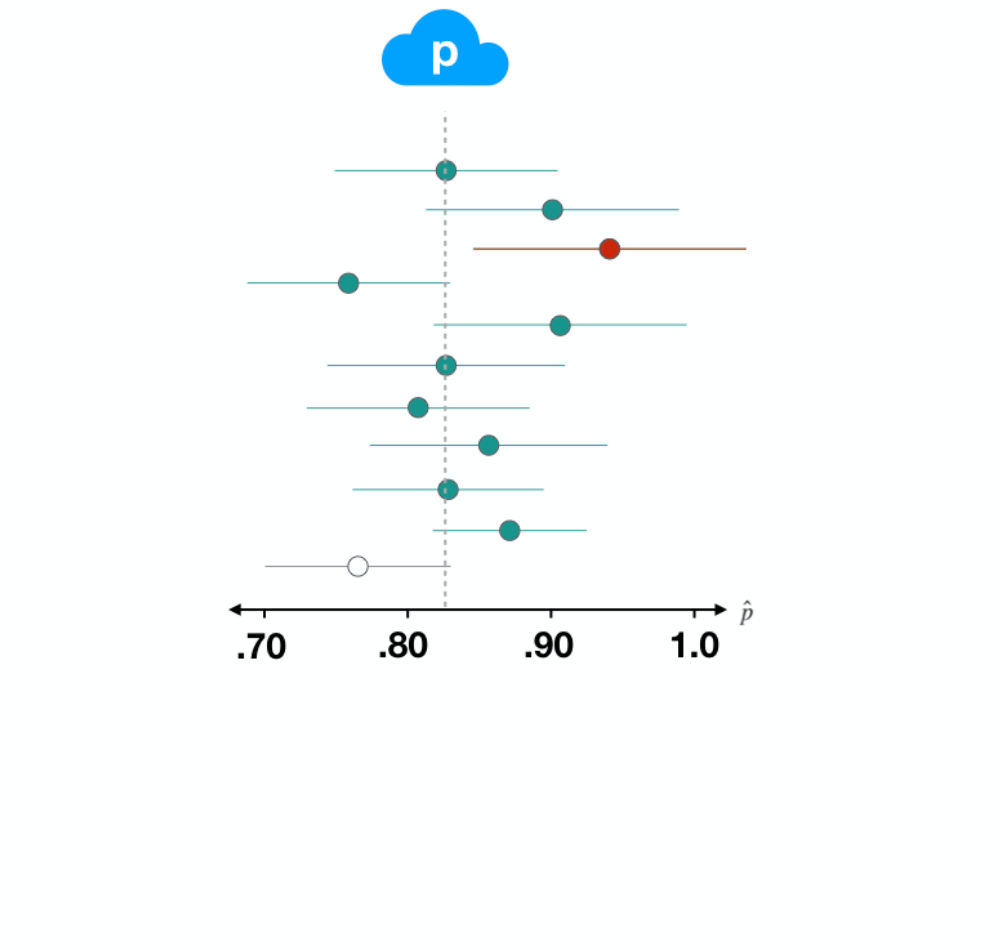
1-2-6.png

Inference for Categorical Data in R

Confidence Intervals

Interpretation: “We’re 95% confident that the true proportion of Americans that are happy is between 0.705 and 0.841.”

Width of the interval affected by

  • n
  • confidence level
  • p
Inference for Categorical Data in R

Let's practice!

Inference for Categorical Data in R

Preparing Video For Download...