Model Estimation and Likelihood

Introduction to Linear Modeling in Python

Jason Vestuto

Data Scientist

Estimation

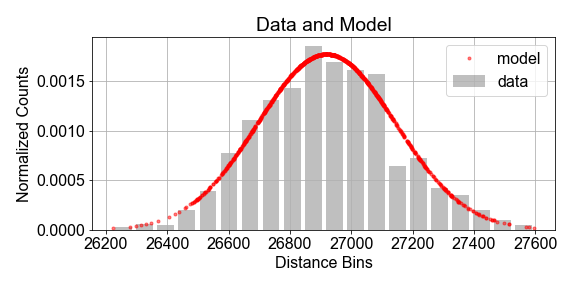
Plot of histogram, normalized counts versus distance bins, of data as grey bars, and of model as red gaussian bell shaped curve fitting closely the top of the grey bars

Estimation

# Define gaussian model function
def gaussian_model(x, mu, sigma):
    coeff_part = 1/(np.sqrt(2 * np.pi * sigma**2))
    exp_part = np.exp( - (x - mu)**2 / (2 * sigma**2) )
    return coeff_part*exp_part

# Compute sample statistics
mean = np.mean(sample)
stdev = np.std(sample)

# Model the population using sample statistics
population_model = gaussian(sample, mu=mean, sigma=stdev)

Likelihood vs Probability

Conditional Probability: $P( \text{outcome A} | \text{given B})$
Probability: $P( \text{data} | \text{model} )$
Likelihood: $L( \text{model} | \text{data} )$

Computing Likelihood

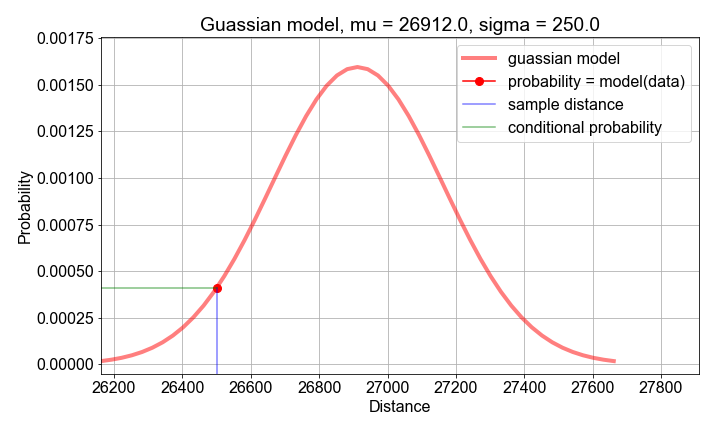
Plot of probability versus distance, as a red gaussian bell shaped curve, with a point near the left edge, and horizontal and vertical line segments connecting this point to each axis

Computing Likelihood

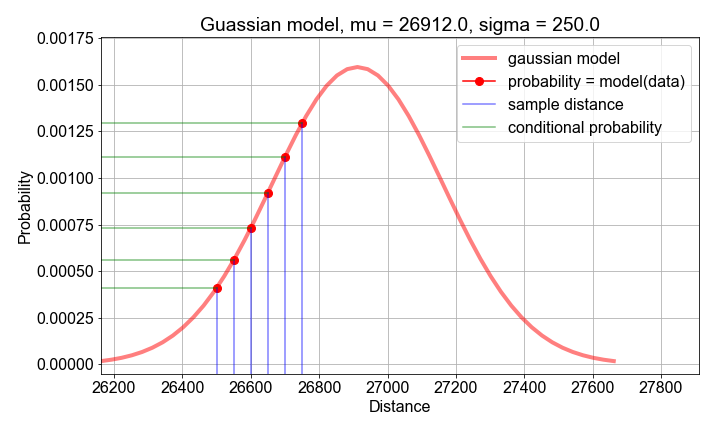
Plot of probability versus distance, as a red gaussian bell shaped curve, with 6 points from the left edge toward the center, with horizontal and vertical line segments connecting each point to both axes

Likelihood from Probabilities

# Guess parameters
mu_guess = np.mean(sample_distances)
sigma_guess = np.std(sample_distances)

# For each sample point, compute a probability
probabilities = np.zeros(len(sample_distances))
for n, distance in enumerate(sample_distances):
    probabilities[n] = gaussian_model(distance, mu=mu_guess, sigma=sigma_guess)

likelihood = np.product(probs)
loglikelihood = np.sum(np.log(probs))

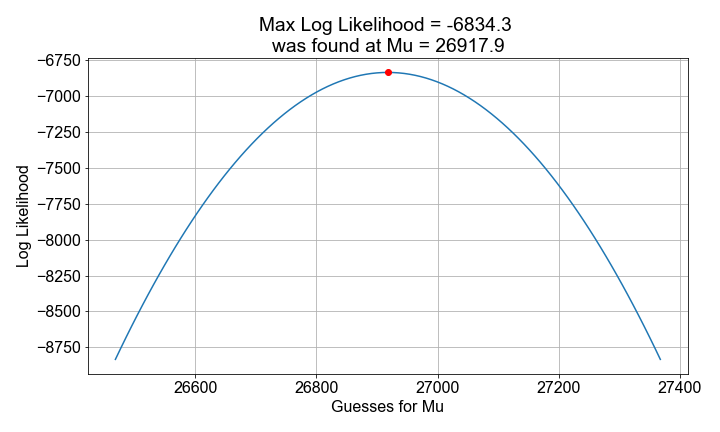
Maximum Likelihood Estimation

# Create an array of mu guesses
low_guess = sample_mean - 2*sample_stdev
high_guess = sample_mean + 2*sample_stdev
mu_guesses = np.linspace(low_guess, high_guess, 101)

# Compute the loglikelihood for each guess
loglikelihoods = np.zeros(len(mu_guesses))
for n, mu_guess in enumerate(mu_guesses):
    loglikelihoods[n] = compute_loglikelihood(sample_distances, mu=mu_guess, sigma=sample_stdev)

# Find the best guess
max_loglikelihood = np.max(loglikelihoods)
best_mu = mu_guesses[loglikelihoods == max_loglikelihood]

Maximum Likelihood Estimation

Plot of down-turned parabola, with red point at the maximum, plotted on axes loglikelihood versus values of mu

Let's practice!

Introduction to Linear Modeling in Python