Quantifying Linear Relationships

Introduction to Linear Modeling in Python

Jason Vestuto

Data Scientist

Pre-Visualization

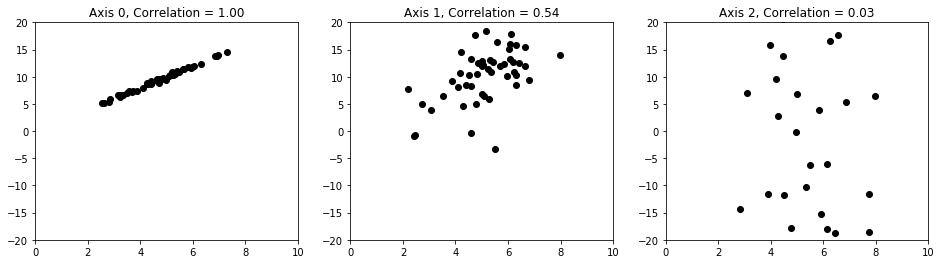
3 panel figure, 3 scatter plots, strong to zero correlation, left to right

Introduction to Linear Modeling in Python

Review of Single Variable Statistics

# Mean
mean = sum(x)/len(x)

# Deviation, sometimes called "centering"
dx = x - np.mean(x)

# Variance
variance = np.mean(dx*dx)

# Standard Deviation
stdev = np.sqrt(variance)
Introduction to Linear Modeling in Python

Covariance

# Deviations of two variables
dx = x - np.mean(x)
dy = y - np.mean(y)

# Co-vary means to vary together
deviation_products = dx*dy

# Covariance as the mean
covariance = np.mean(dx*dy)
Introduction to Linear Modeling in Python

Correlation

# Divide deviations by standard deviation 
zx = dx/np.std(x)
zy = dy/np.std(y)

# Mean of the normalize deviations
correlation = np.mean(zx*zy)
Introduction to Linear Modeling in Python

Normalization: Before

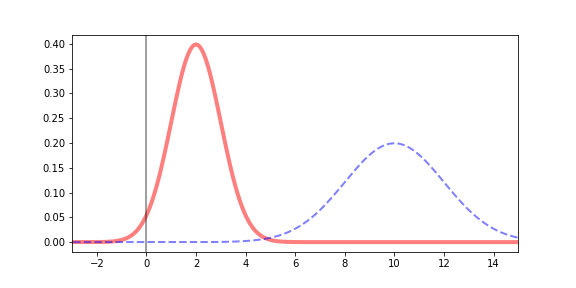
Plot of gaussian distributions, bell shaped, with different centers, heights, and widths

Introduction to Linear Modeling in Python

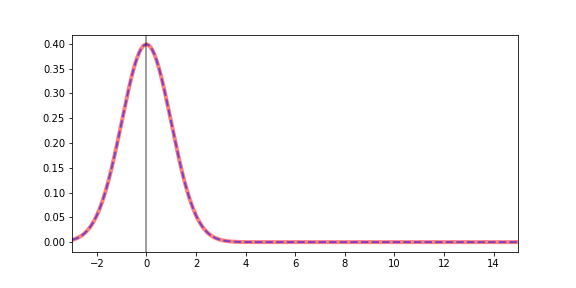
Normalization: After

Plot of gaussian distributions, bell shaped, both centered on zero, with the same height and width

Introduction to Linear Modeling in Python

Magnitude versus Direction

  • Correlation values: -1 to +1

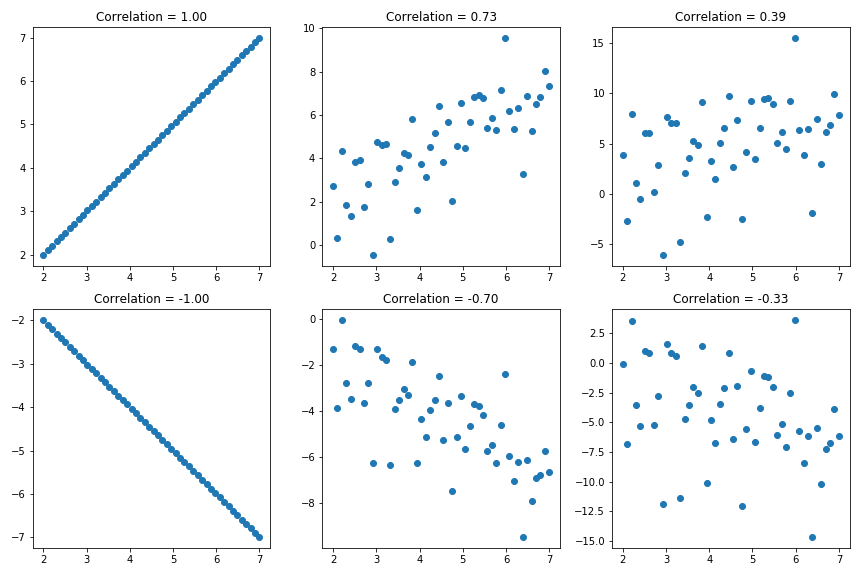
6 panel figure, 2 rows of 3 columns, scatter plots, stronger to weaker correlation from left to right

  • Two Parts: Magnitude (1 to 0) versus Sign (+ or -)
Introduction to Linear Modeling in Python

Let's practice!

Introduction to Linear Modeling in Python

Preparing Video For Download...