Assessing model fit with R-squared

Modeling with Data in the Tidyverse

Albert Y. Kim

Assistant Professor of Statistical and Data Sciences

R-squared

$R^2 = 1 - \frac{\text{Var}(\text{residuals})}{\text{Var}(y)}$

$R^2$ is between 0 & 1
Smaller $R^2$ ~ "poorer fit"
$R^2 = 1$ ~ "perfect fit" and $R^2 = 0$ ~ "no fit"

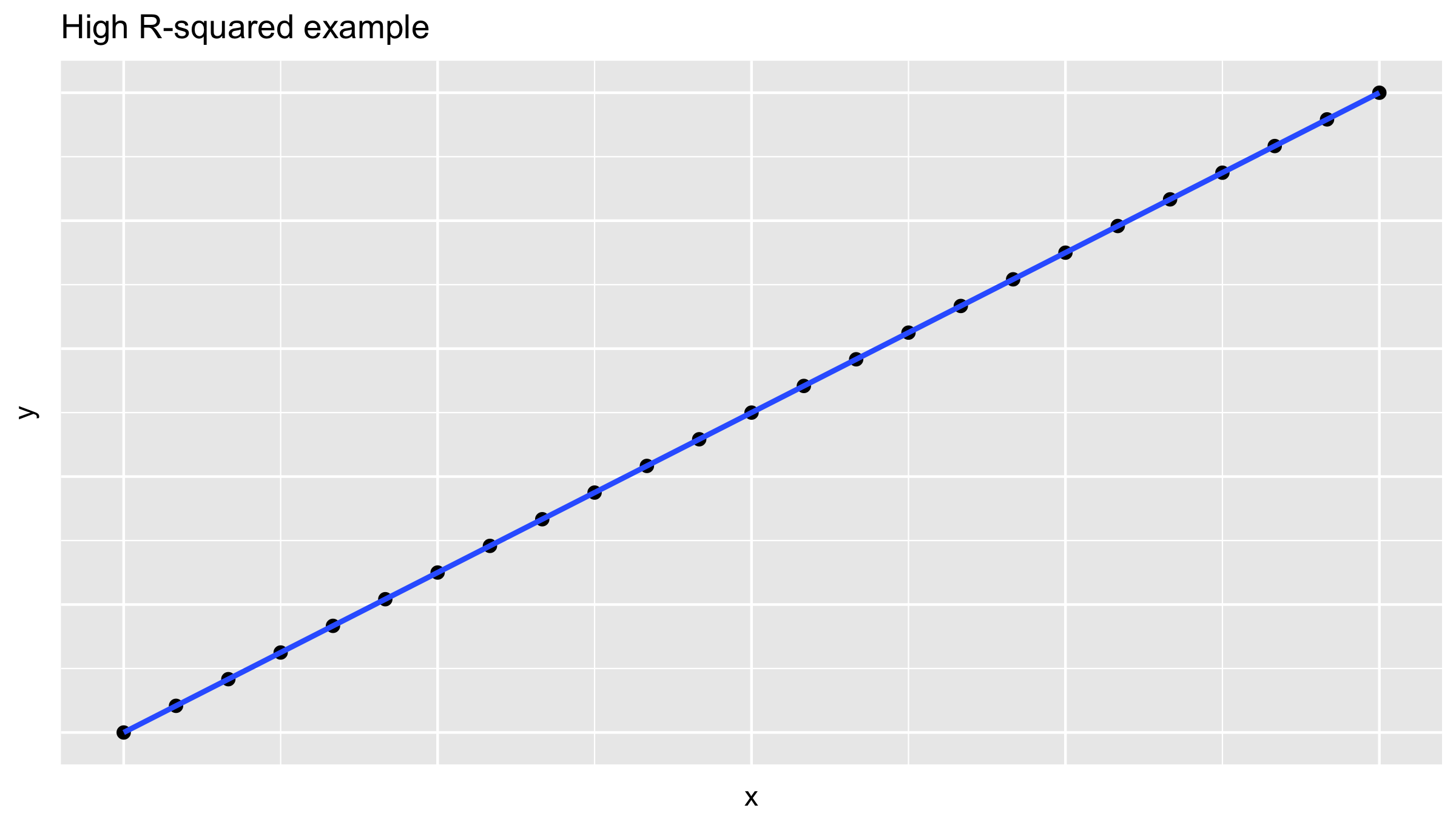
High R-squared value example

$R^2 = 1 - \frac{\text{Var}(\text{residuals})}{\text{Var}(y)}$

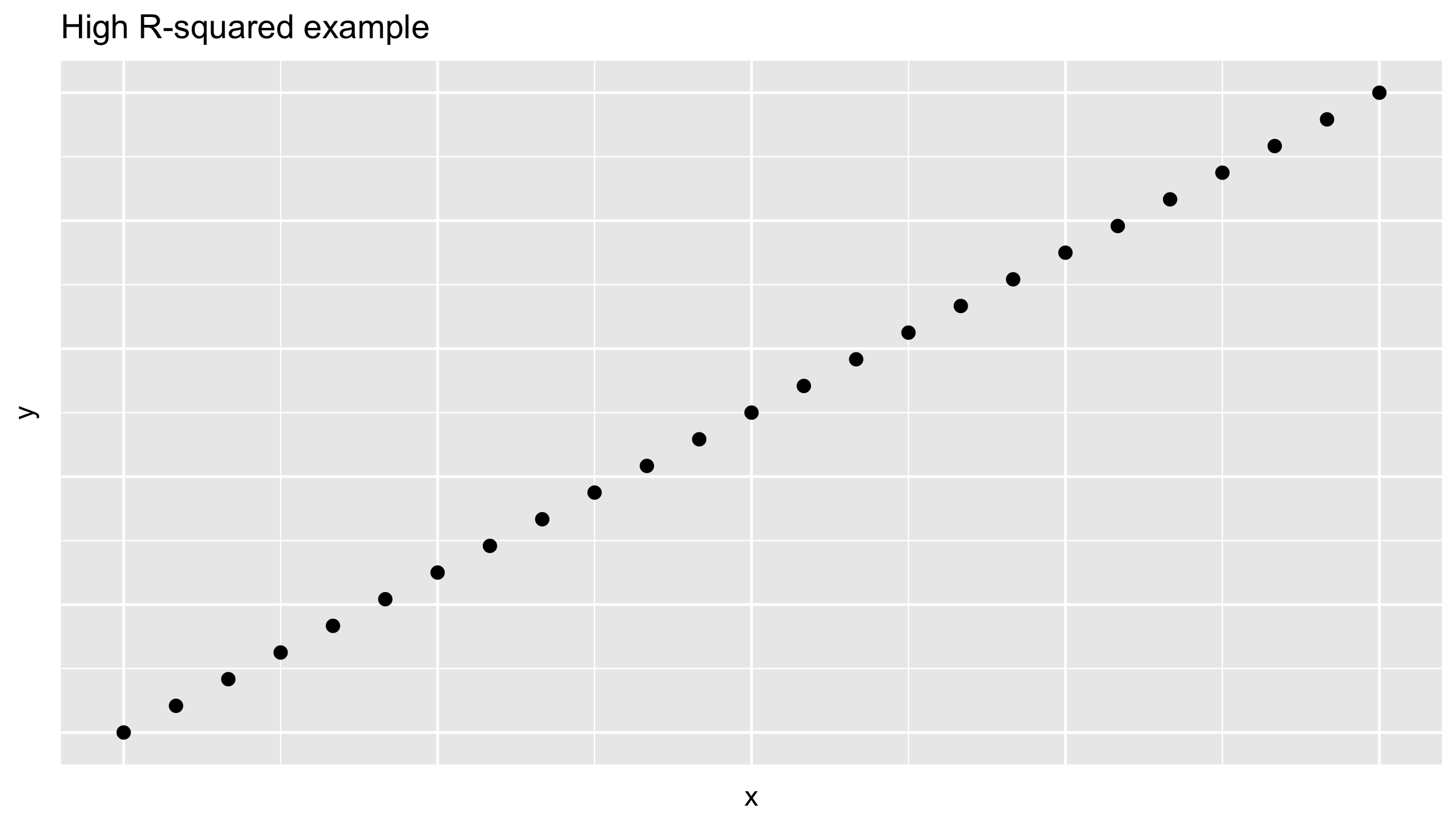
High R-squared value: "Perfect" fit

$R^2 = 1 - \frac{\text{Var}(\text{residuals})}{\text{Var}(y)}$

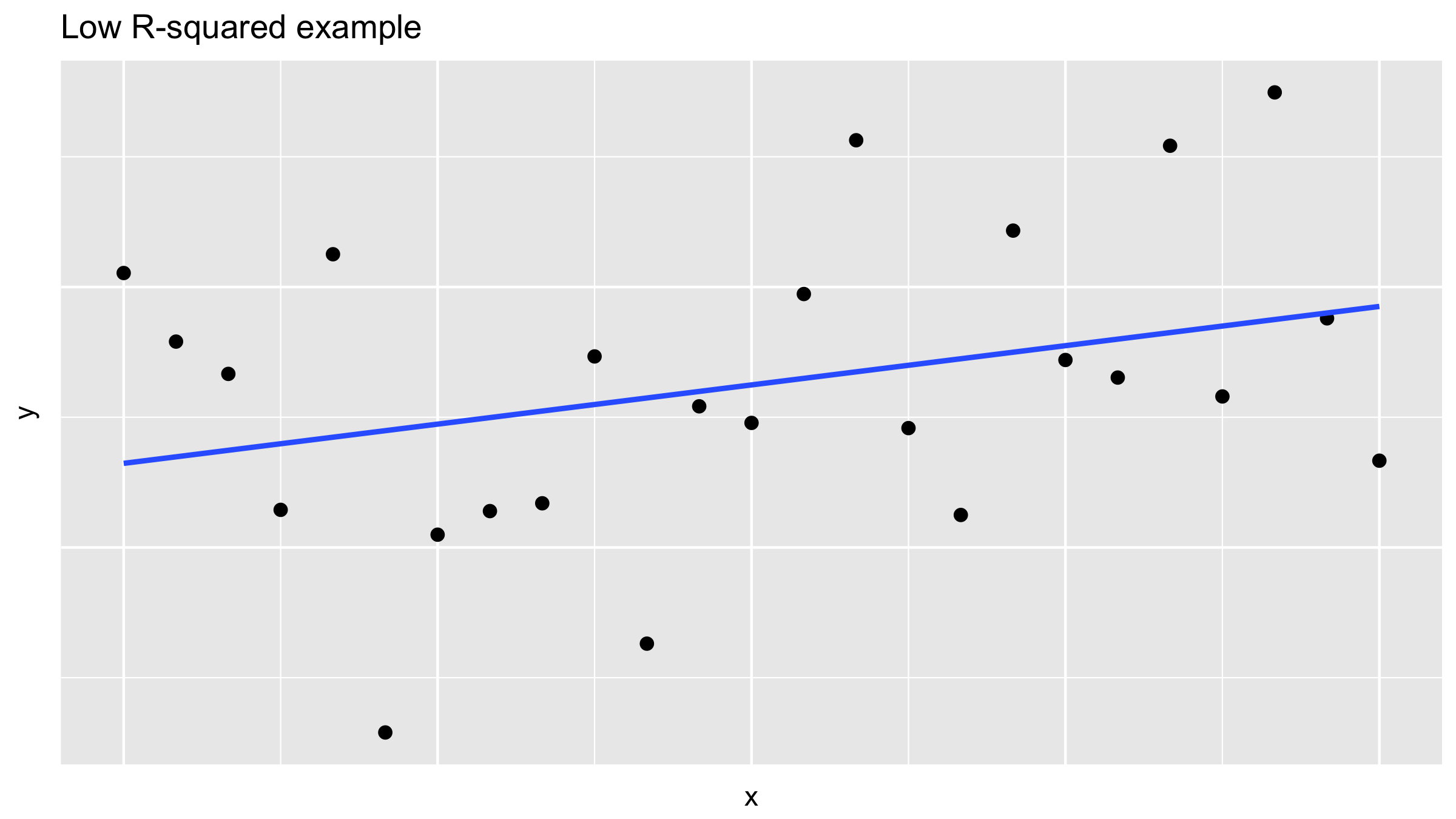
Low R-squared value example

$R^2 = 1 - \frac{\text{Var}(\text{residuals})}{\text{Var}(y)}$

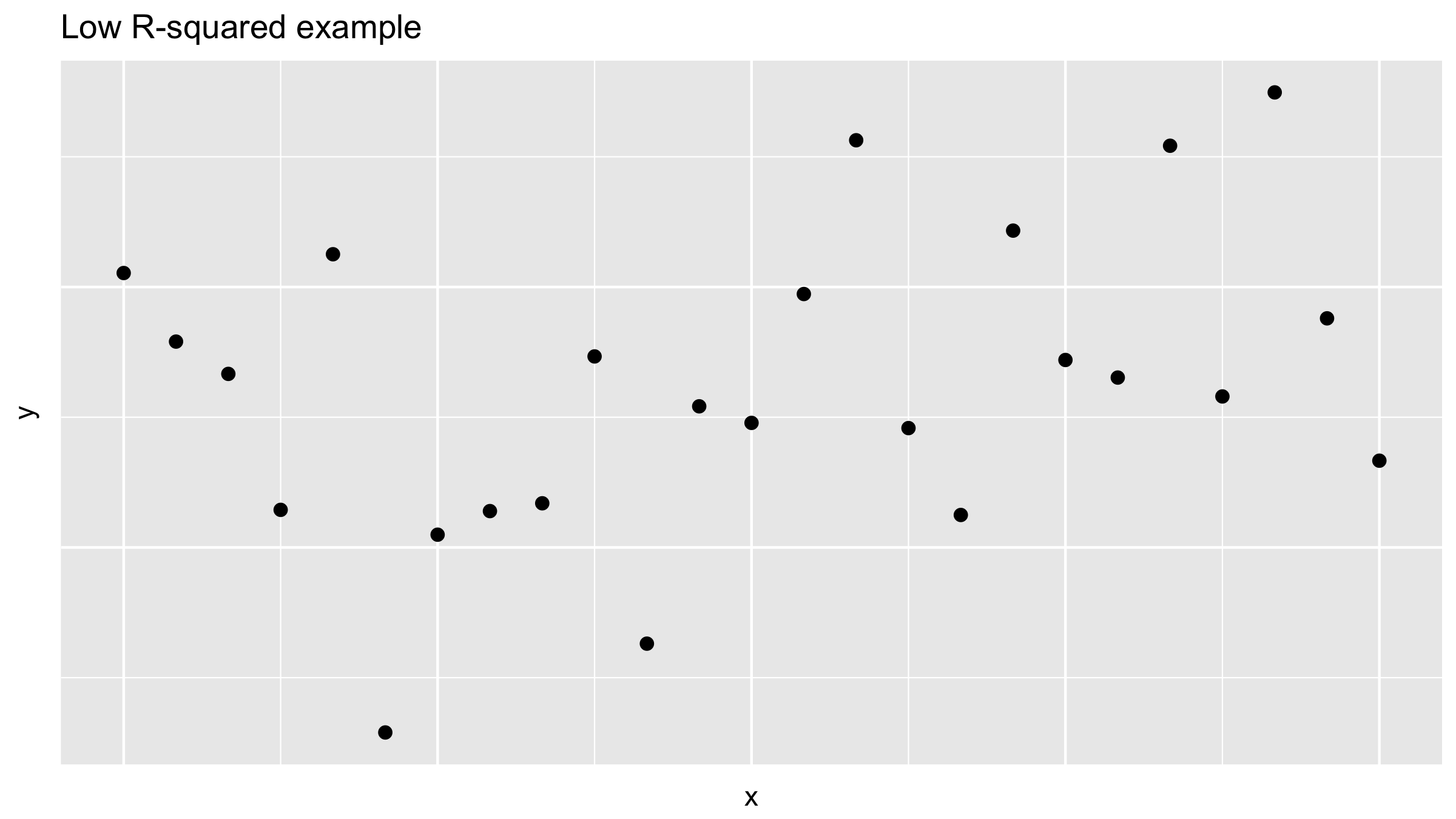
Low R-squared value example

$R^2 = 1 - \frac{\text{Var}(\text{residuals})}{\text{Var}(y)}$

Numerical interpretation

Since $\text{Var}(y) \geq \text{Var}(\text{residuals})$ and $$

$R^2 = 1 - \frac{\text{Var}(\text{residuals})}{\text{Var}(y)} = \frac{\text{Var}(y) - \text{Var}(\text{residuals})}{\text{Var}(y)}$

$R^2$'s interpretation is: the proportion of the total variation in the outcome variable $y$ that the model explains.

Computing R-squared

# Model 1: price as a function of size and year built
model_price_1 <- lm(log10_price ~ log10_size + yr_built,
                    data = house_prices)

get_regression_points(model_price_1) %>%
  summarize(r_squared = 1 - var(residual)/var(log10_price))

# A tibble: 1 x 1
  r_squared
      <dbl>
1     0.483

Computing R-squared

# Model 3: price as a function of size and condition
model_price_3 <- lm(log10_price ~ log10_size + condition,
                    data = house_prices)

get_regression_points(model_price_3) %>%
  summarize(r_squared = 1 - var(residual)/var(log10_price))

# A tibble: 1 x 1
  r_squared
      <dbl>
1     0.462

Let's practice!

Modeling with Data in the Tidyverse