Background on modeling for explanation

Modeling with Data in the Tidyverse

Albert Y. Kim

Assistant Professor of Statistical and Data Sciences

Course overview

Introduction to modeling: theory and terminology
Regression:
- Simple linear regression
- Multiple regression
Model assessment

General modeling framework formula

$$y = f(\vec{x}) + \epsilon$$

Where:

$y$: outcome variable of interest
$\vec{x}$: explanatory/predictor variables
$f()$: function of the relationship between $y$ and $\vec{x}$ AKA the signal
$\epsilon$: unsystematic error component AKA the noise

Two modeling scenarios

Modeling for either:

Explanation: $\vec{x}$ are explanatory variables
Prediction: $\vec{x}$ are predictor variables

Modeling for explanation example

A University of Texas in Austin study on teaching evaluation scores (available at openintro.org).

Question: Can we explain differences in teaching evaluation score based on various teacher attributes?

Variables:

$y$: Average teaching score based on students evaluations
$\vec{x}$: Attributes like rank, gender, age, and bty_avg

Modeling for explanation example

From the moderndive package for ModernDive.com:

library(dplyr)
library(moderndive)
glimpse(evals)

Observations: 463
Variables: 13
$ ID           <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10...
$ score        <dbl> 4.7, 4.1, 3.9, 4.8, 4.6, 4.3...
$ age          <int> 36, 36, 36, 36, 59, 59, 59, 51...
$ bty_avg      <dbl> 5.000, 5.000, 5.000, 5.000...
$ gender       <fct> female, female, female, female...
...

Exploratory data analysis

Three basic steps to exploratory data analysis (EDA):

Looking at your data
Creating visualizations
Computing summary statistics

Exploratory data analysis

library(ggplot2)
ggplot(evals, aes(x = score)) +
  geom_histogram(binwidth = 0.25) + 
  labs(x = "teaching score", y = "count")

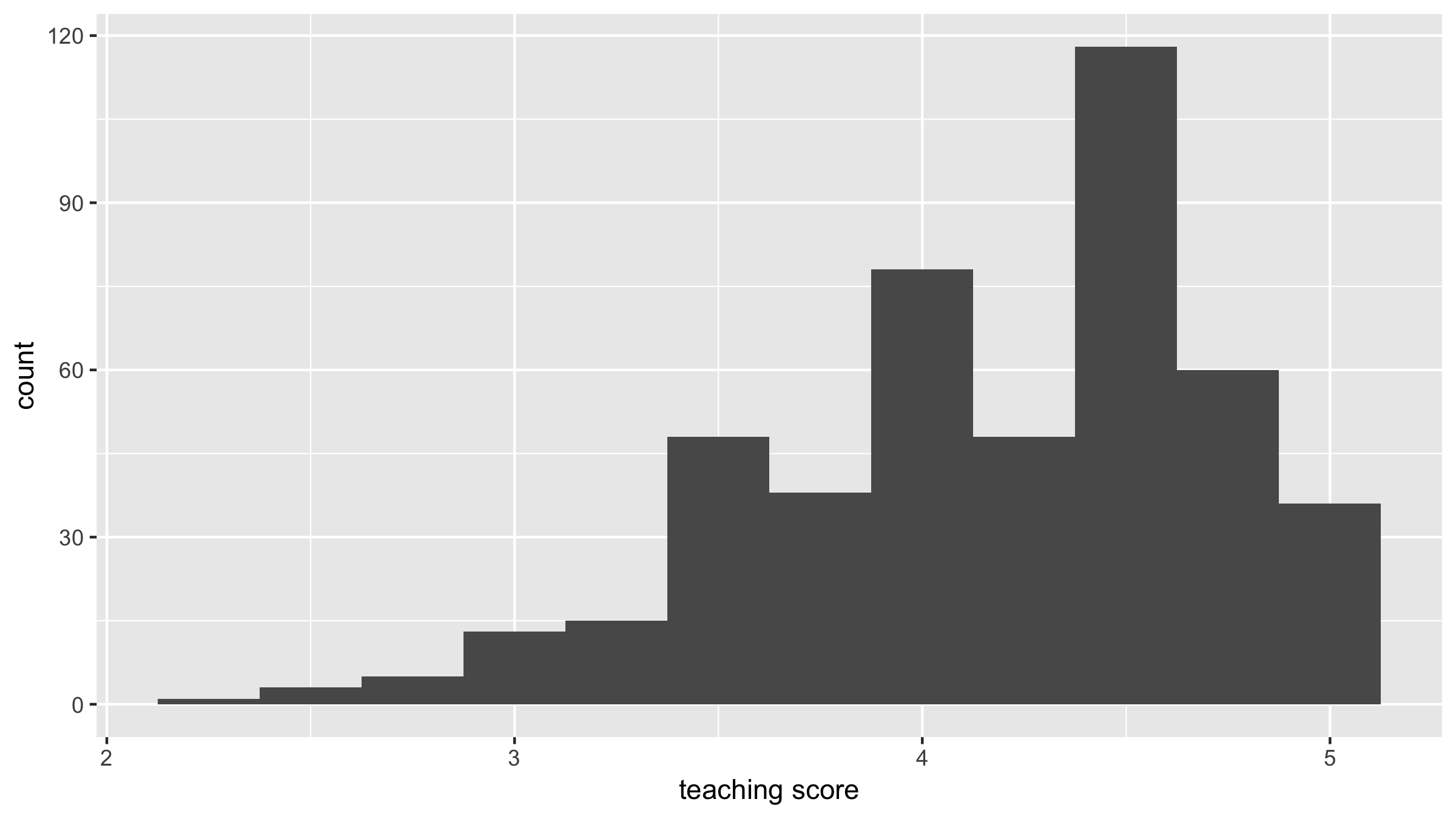
Exploratory data analysis

# Compute mean, median, and standard deviation
evals %>%
  summarize(mean_score = mean(score), 
            median_score = median(score),
            sd_score = sd(score))

# A tibble: 1 x 3
  mean_score median_score sd_score
       <dbl>        <dbl>    <dbl>
1       4.17          4.3    0.544

Let's practice!

Modeling with Data in the Tidyverse