Predicting teaching score using age

Modeling with Data in the Tidyverse

Albert Y. Kim

Assistant Professor of Statistical and Data Sciences

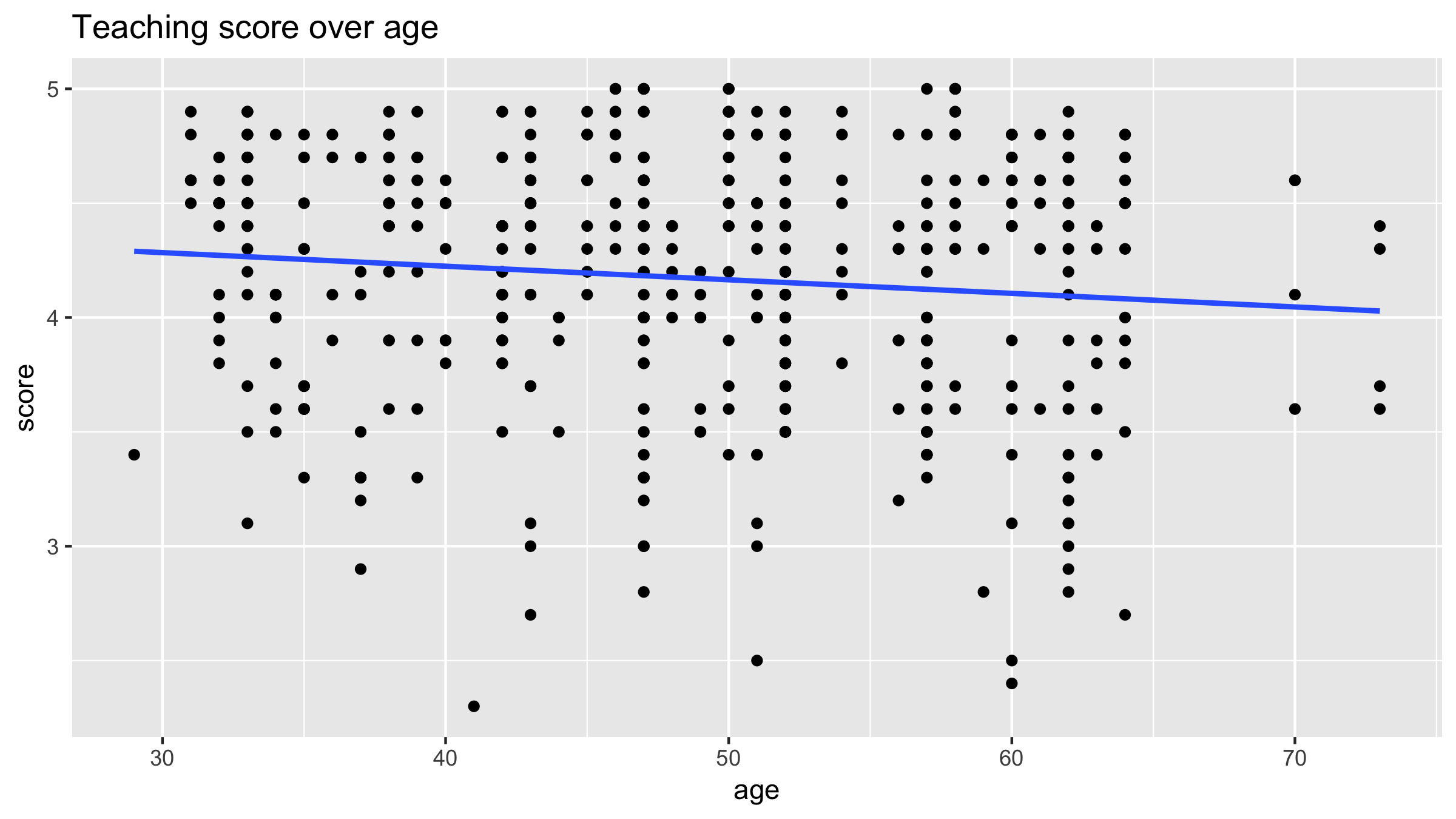
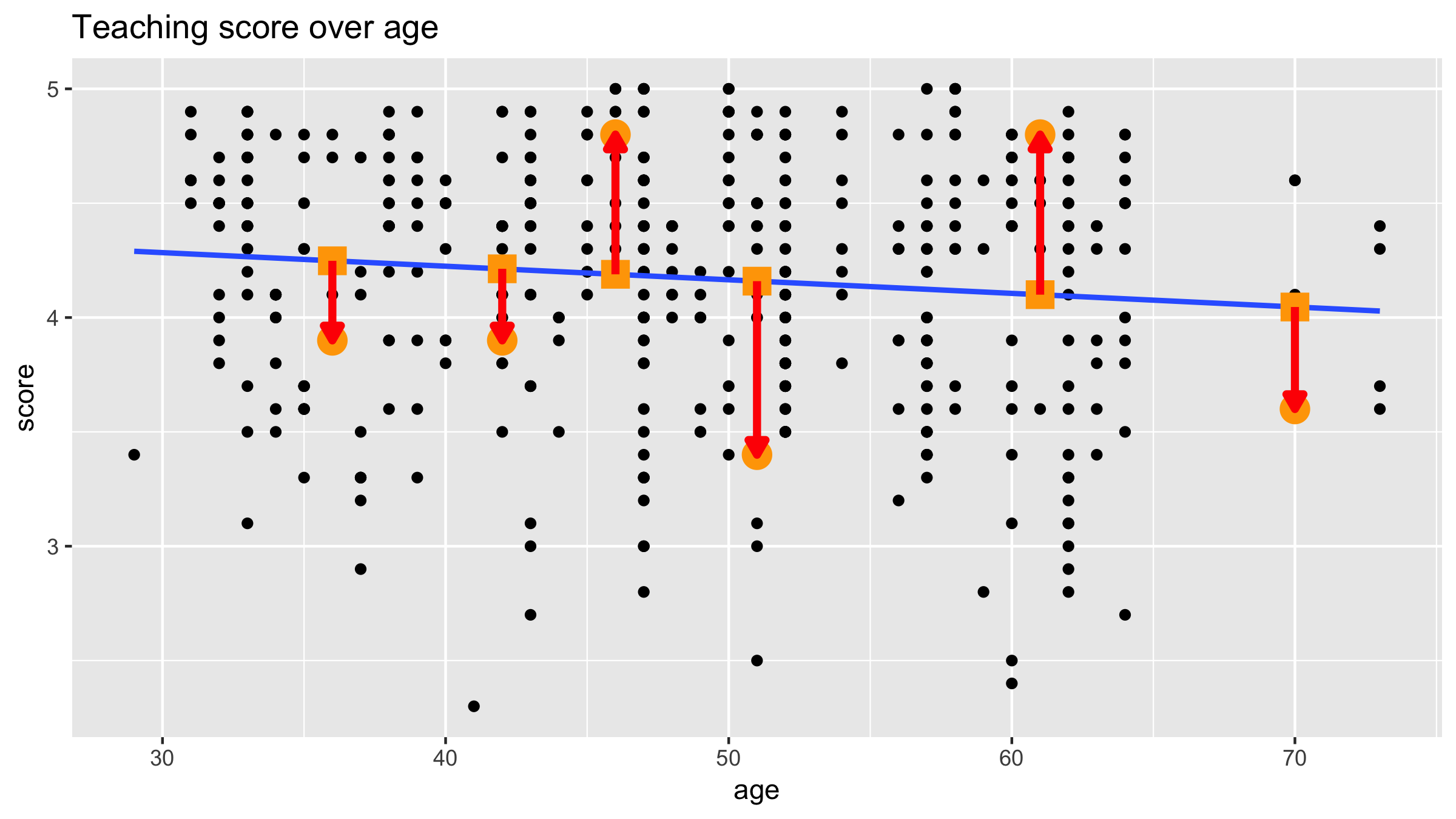
Refresher: Regression line

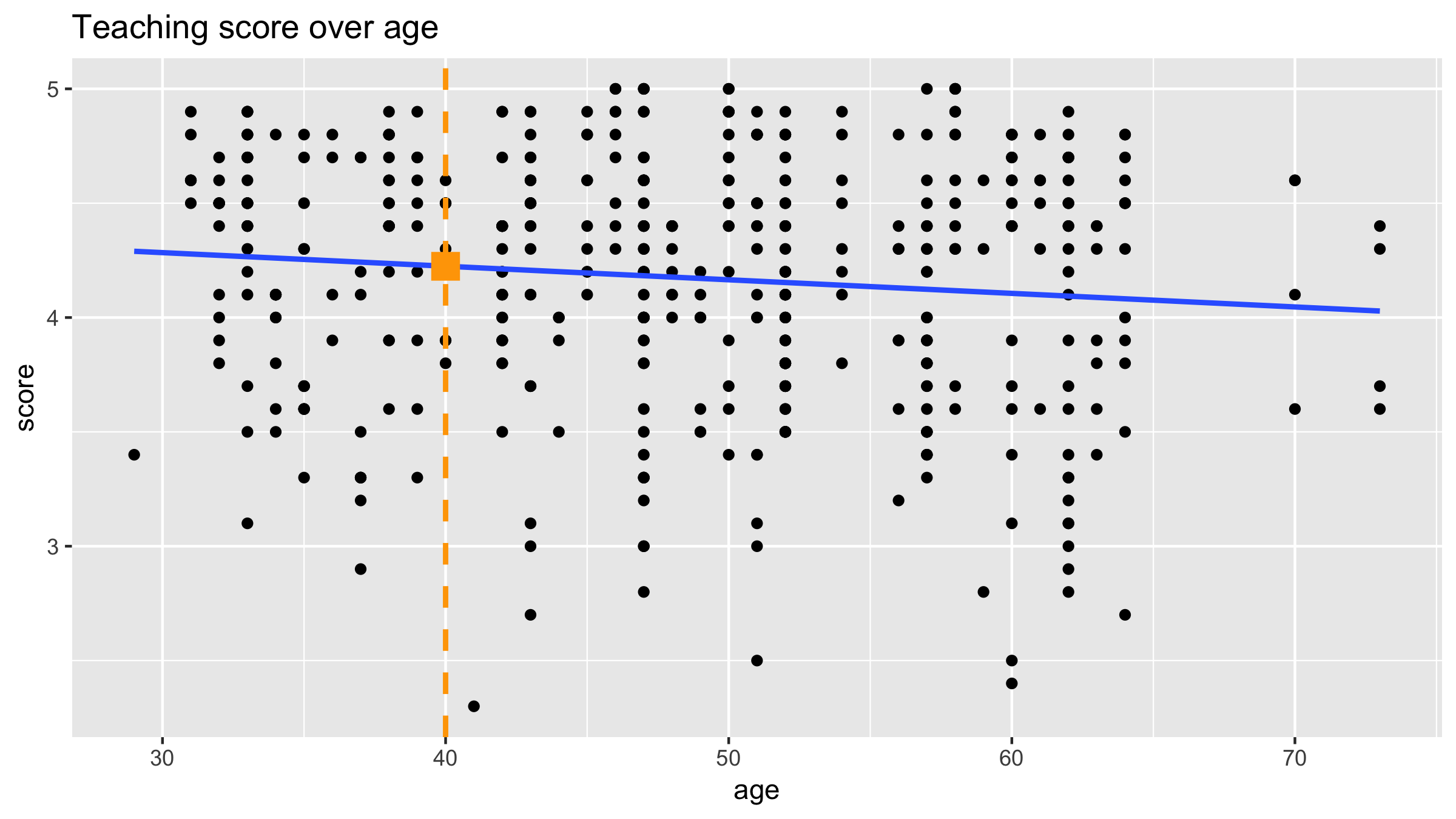
New instructor prediction

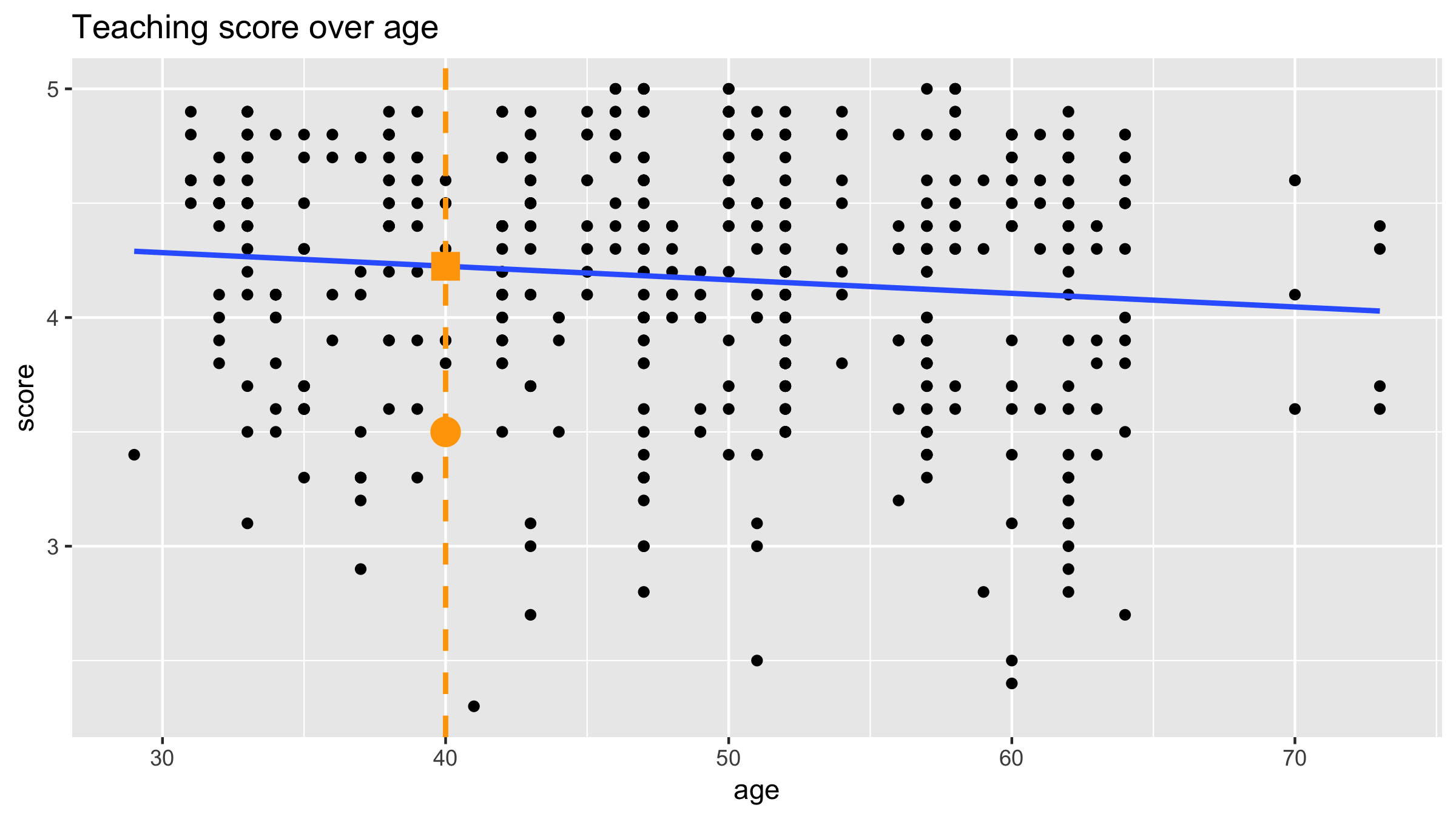
Refresher: Regression table

library(ggplot2)
library(dplyr)
library(moderndive)

# Fit regression model using formula of form: y ~ x
model_score_1 <- lm(score ~ age, data = evals)

# Output regression table using wrapper function
get_regression_table(model_score_1)

# A tibble: 2 x 7
  term      estimate std_error statistic p_value lower_ci...
  <chr>        <dbl>     <dbl>     <dbl>   <dbl>    <dbl>...
1 intercept    4.46      0.127     35.2    0        4.21...
2 age         -0.006     0.003     -2.31   0.021   -0.011...

Predicted value

Predictive regression models in general: $\hat{y} = \hat{f}(x) = \hat{\beta}_0 + \hat{\beta}_1 \cdot x$
Our predictive model: $\hat{\text{score}} = 4.46 - 0.006 \cdot \text{age}$
Our prediction: $4.46 - 0.006 \cdot 40 = 4.22$

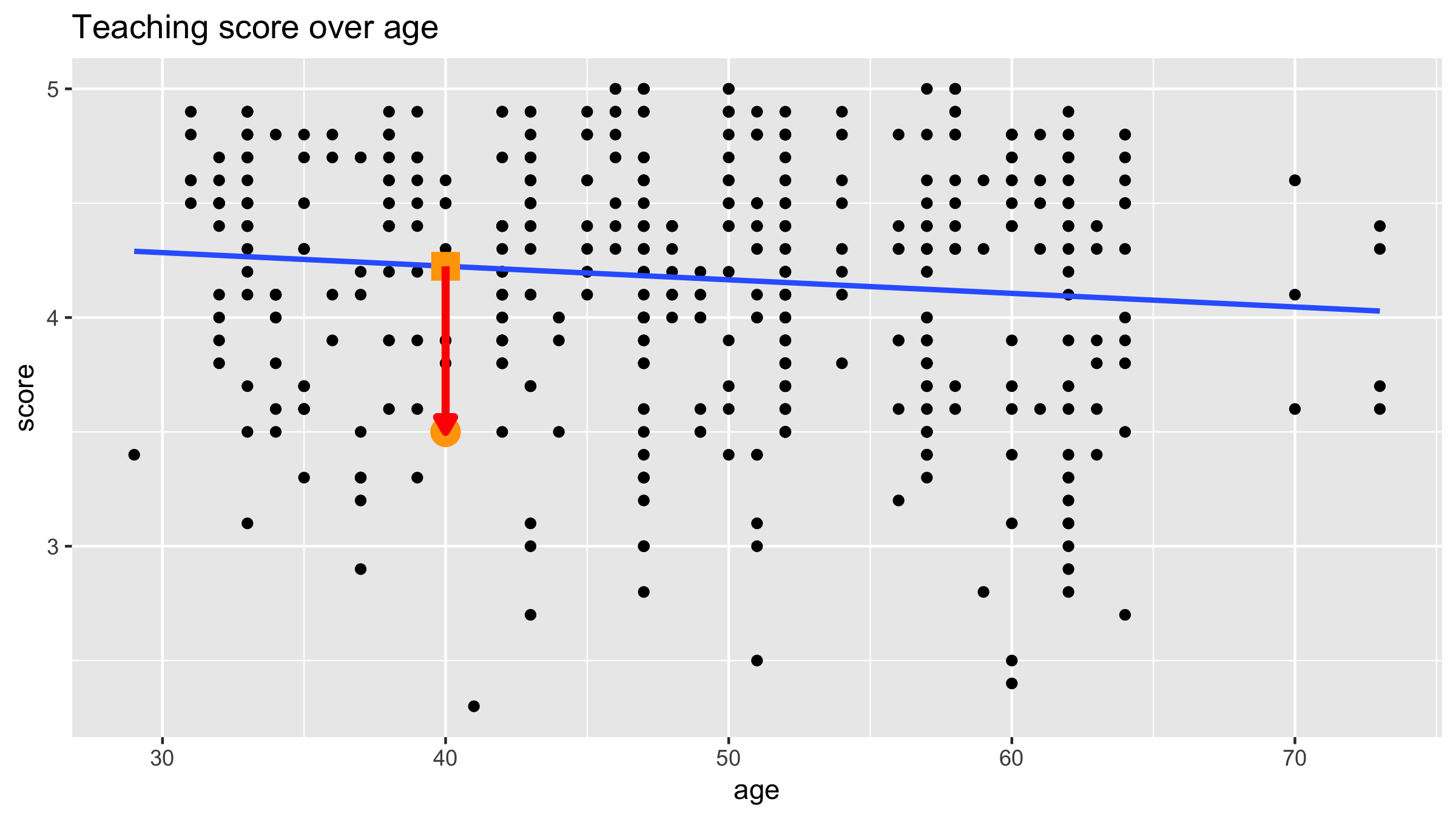
Prediction error

Prediction error

Residuals as model errors

Residual = $y - \hat{y}$
Corresponds to $\epsilon$ from $y = f(\vec{x}) + \epsilon$
For our example instructor: $y - \hat{y} = 3.5 - 4.22 = -0.72$
In linear regression, they are on average 0.

Computing all predicted values

# Fit regression model using formula of form: y ~ x
model_score_1 <- lm(score ~ age, data = evals)

# Get information on each point
get_regression_points(model_score_1)

# A tibble: 463 x 5
      ID score   age score_hat residual
   <int> <dbl> <dbl>     <dbl>    <dbl>
 1     1   4.7    36      4.25    0.452
 2     2   4.1    36      4.25   -0.148
 3     3   3.9    36      4.25   -0.348
 4     4   4.8    36      4.25    0.552
 5     5   4.6    59      4.11    0.488

"Best fitting" regression line

Let's practice!

Modeling with Data in the Tidyverse

Preparing Video For Download...