The modeling problem for prediction

Modeling with Data in the Tidyverse

Albert Y. Kim

Assistant Professor of Statistical and Data Sciences

Modeling problem

Consider $y = f(\vec{x}) + \epsilon$.

$f()$ and $\epsilon$ are unknown
$n$ observations of $y$ and $\vec{x}$ are known/given in the data
Goal: Fit a model $\hat{f}()$ that approximates $f()$ while ignoring $\epsilon$
Goal restated: Separate the signal from the noise
Can then generate fitted/predicted values $\hat{y} = \hat{f}(\vec{x})$

Difference between explanation and prediction

Key difference in modeling goals:

Explanation: We care about the form of $\hat{f}()$, in particular any values quantifying relationships between $y$ and $\vec{x}$
Prediction: We don't care so much about the form of $\hat{f}()$, only that it yields "good" predictions $\hat{y}$ of $y$ based on $\vec{x}$

Condition of house

house_prices %>% 
  select(log10_price, condition) %>% 
  glimpse()

Observations: 21,613
Variables: 2
$ log10_price <dbl> 5.346157, 5.730782, 5.255273...
$ condition   <fct> 3, 3, 3, 5, 3, 3, 3, 3, 3, 3, 3...

Exploratory data visualization: boxplot

library(ggplot2)
library(dplyr)
library(moderndive)

# Apply log10-transformation to outcome variable
house_prices <- house_prices %>%
  mutate(log10_price = log10(price))

# Boxplot
ggplot(house_prices, aes(x = condition, y = log10_price)) +
  geom_boxplot() +
  labs(x = "house condition", y = "log10 price", 
       title = "log10 house price over condition")

Exploratory data visualization: boxplot

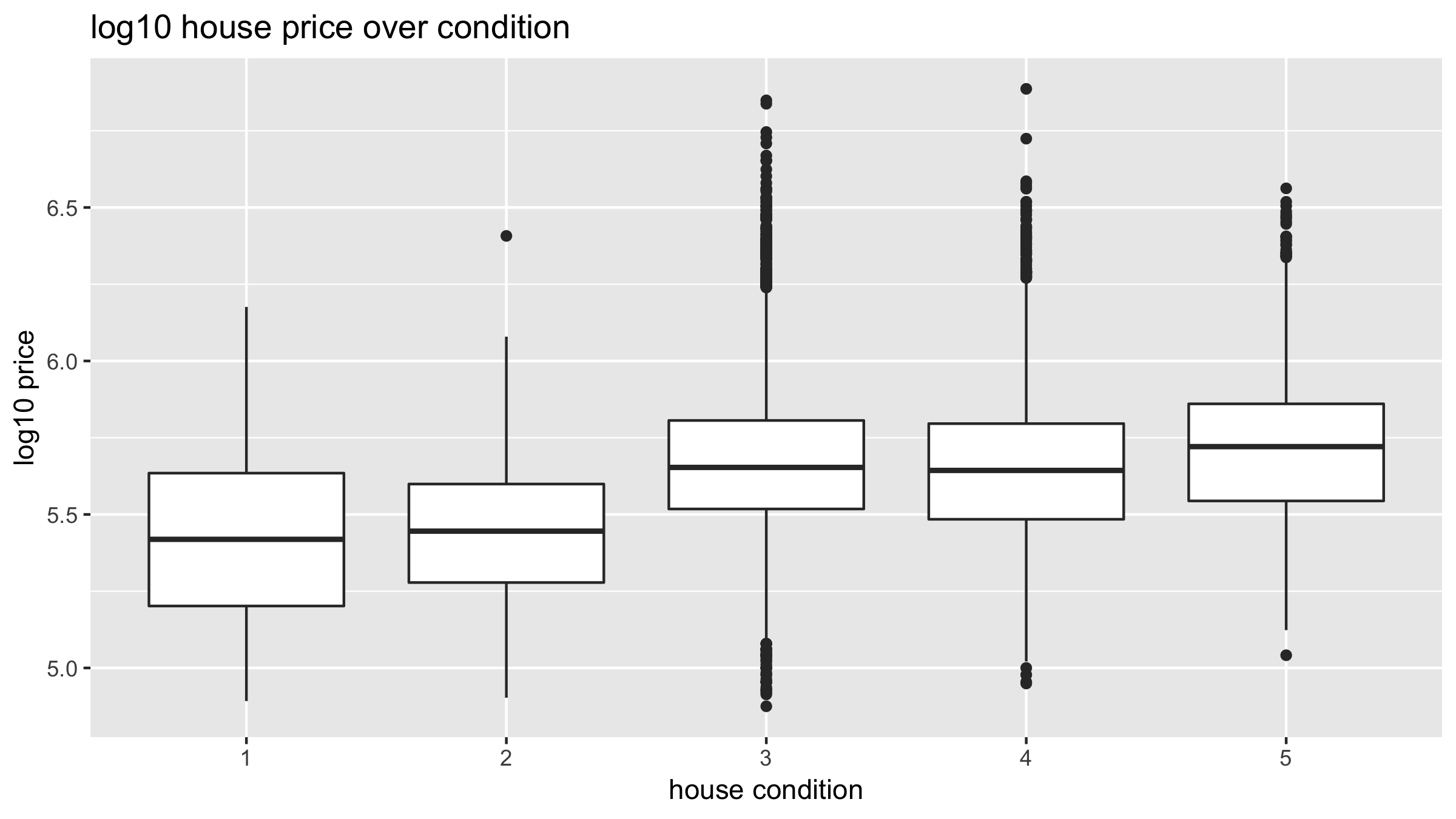
Exploratory data summaries

house_prices %>% 
  group_by(condition) %>% 
  summarize(mean = mean(log10_price),
            sd = sd(log10_price), n = n())

# A tibble: 5 x 4
  condition  mean    sd     n
  <fct>     <dbl> <dbl> <int>
1 1          5.42 0.293    30
2 2          5.45 0.233   172
3 3          5.67 0.224 14031
4 4          5.65 0.228  5679
5 5          5.71 0.244  1701

Exploratory data summaries

# Prediction for new house with condition 4 in dollars
10^(5.65)

446683.6

Let's practice!

Modeling with Data in the Tidyverse