The modeling problem for explanation

Modeling with Data in the Tidyverse

Albert Y. Kim

Assistant Professor of Statistical and Data Sciences

Recall: General modeling framework formula

$$ y = f(\vec{x}) + \epsilon $$

Where:

$y$: outcome variable of interest
$\vec{x}$: explanatory/predictor variables
$f()$: function of the relationship between $y$ and $\vec{x}$ AKA the signal
$\epsilon$: unsystematic error component AKA the noise

The modeling problem

Consider $y = f(\vec{x}) + \epsilon$.

$f()$ and $\epsilon$ are unknown
$n$ observations of $y$ and $\vec{x}$ are known/given in the data
Goal: Fit a model $\hat{f}()$ that approximates $f()$ while ignoring $\epsilon$
Goal restated: Separate the signal from the noise
Can then generate fitted/predicted values $\hat{y} = \hat{f}(\vec{x})$

Modeling for explanation example

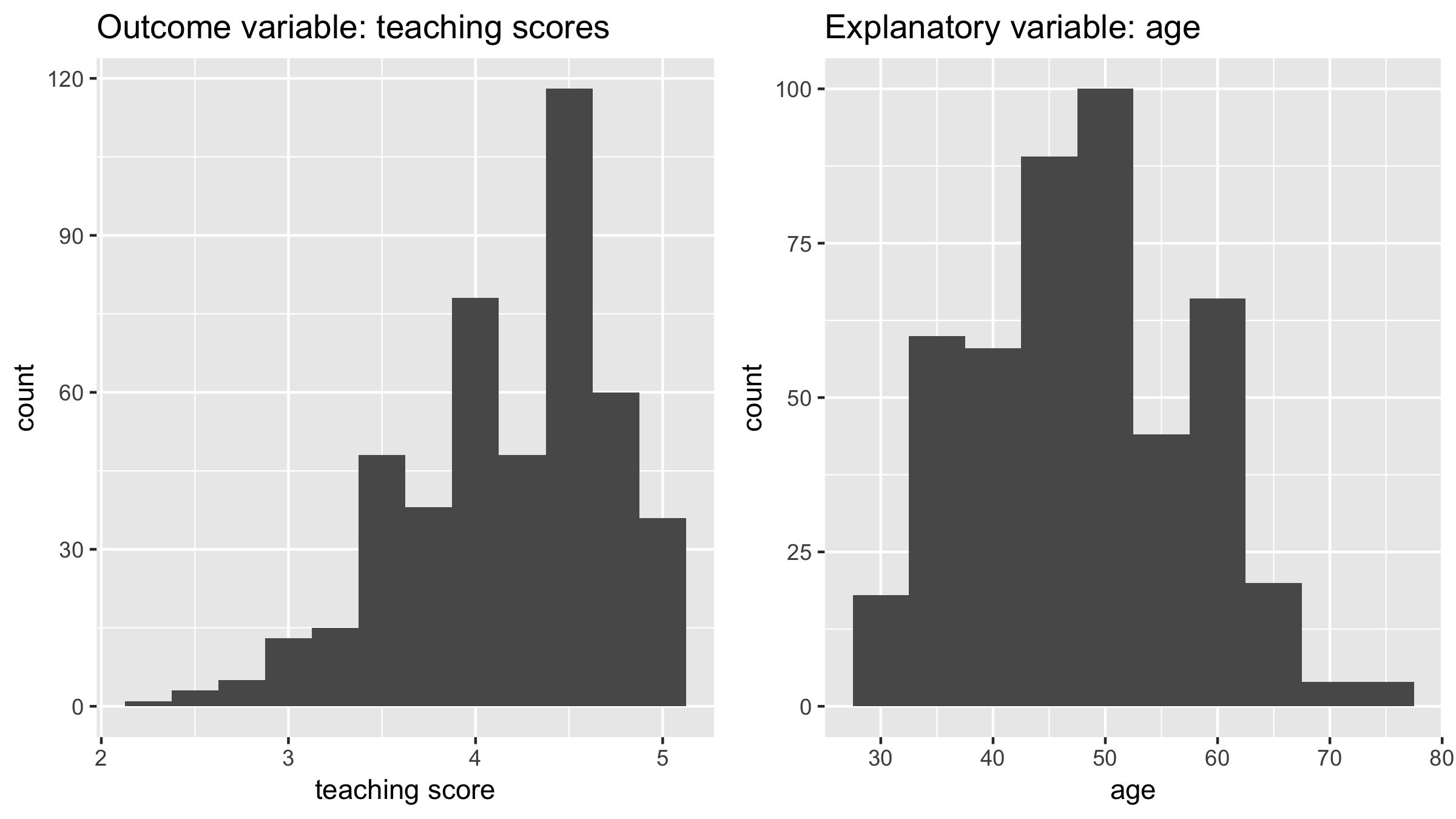
EDA of relationship

library(ggplot2)
library(dplyr)
library(moderndive)

ggplot(evals, aes(x = age, y = score)) +
  geom_point() + 
  labs(x = "age", y = "score",
       title = "Teaching score over age")

EDA of relationship

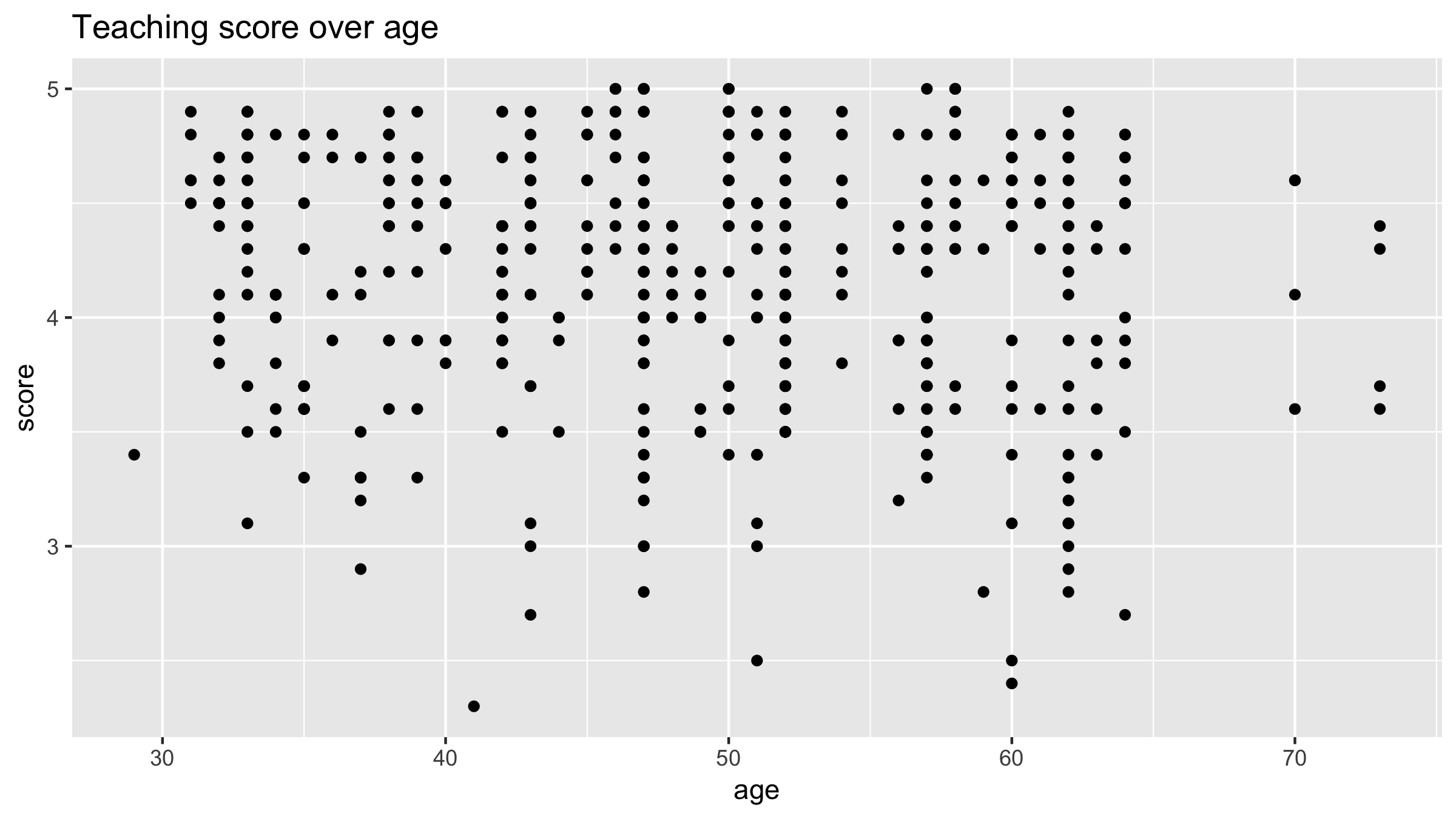
Jittered scatterplot

library(ggplot2)
library(dplyr)
library(moderndive)

# Use geom_jitter() instead of geom_point()
ggplot(evals, aes(x = age, y = score)) +
  geom_jitter() + 
  labs(x = "age", y = "score",
       title = "Teaching score over age (jittered)")

Jittered scatterplot

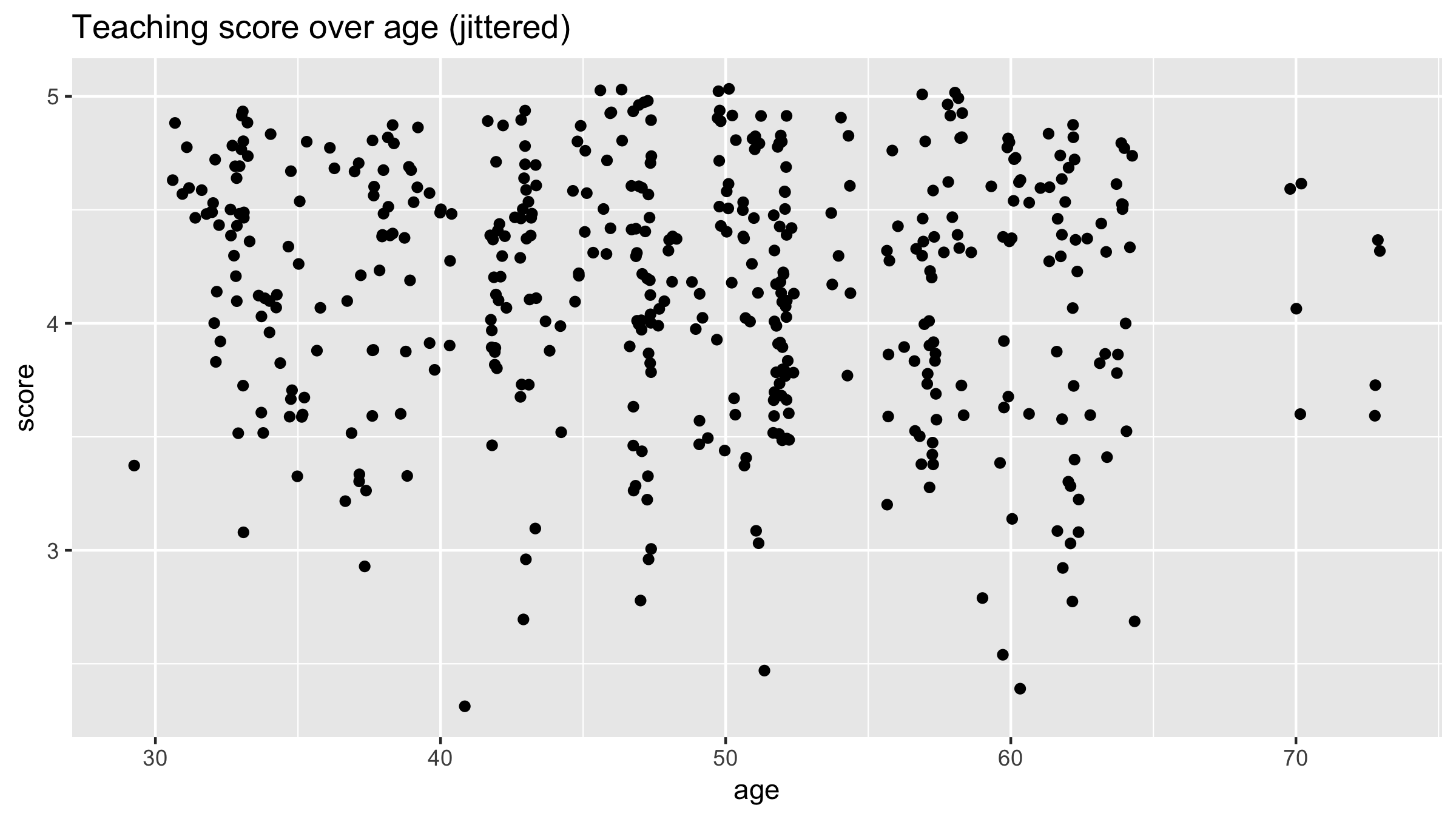
Correlation coefficient

Computing the correlation coefficient

evals %>% 
  summarize(correlation = cor(score, age))

# A tibble: 1 x 1
  correlation
        <dbl>
1      -0.107

Let's practice!

Modeling with Data in the Tidyverse