Transfer Functions & Ensembling

Forecasting Product Demand in R

Aric LaBarr, Ph.D.

Senior Data Scientist, Elder Research

Combining Techniques

Multiple ways to combine forecasting techniques:
1. Transfer Functions - everything gets built into one model
2. Ensembling - "Average" multiple types of model forecasts

Combining Techniques - Transfer Functions

Combining Forecasts

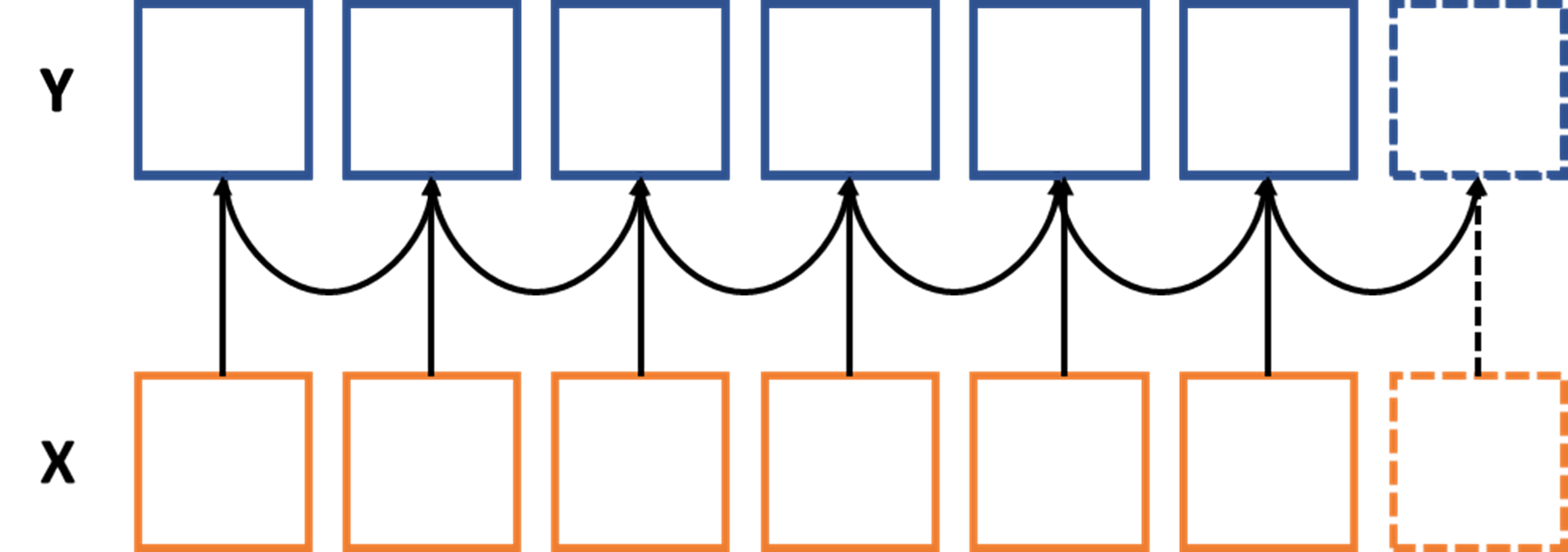
Mathematics in the Background

Combining two different techniques into one mathematically:

$$ \log(Y_{t}) = \beta_0 + \beta_1 \log(X_{t}) + \beta_2 X_{2} + ... + \varepsilon_{t} $$

$$ \varepsilon_{t} = \alpha_0 + \alpha_1 \varepsilon_{t-1} + \alpha_2 \varepsilon_{t-2} + ... + \epsilon $$

Combining the forecasts into one mathematically:

$$ \log(Y_{t}) = \log( \hat{Y_{t}} ) + \hat{\varepsilon_{t}} $$

$$ Y_{t} = \hat{Y_{t}} \times \exp(\hat{\varepsilon}) $$

Transfer Function Example

for_M_hi_arima <- exp(for_M_hi_arima)
for_M_hi_final <- pred_M_hi_xts * for_M_hi_arima

M_hi_v <- bev_xts_valid[,"M.hi"]

MAE <- mean(abs(for_M_hi_final - M_hi_v))
MAPE <- 100*mean(abs((for_M_hi_final - M_hi_v)/M_hi_v))

print(MAE)

[1] 61.46033

print(MAPE)

[1] 13.45189

Combining Forecasts - Ensembling

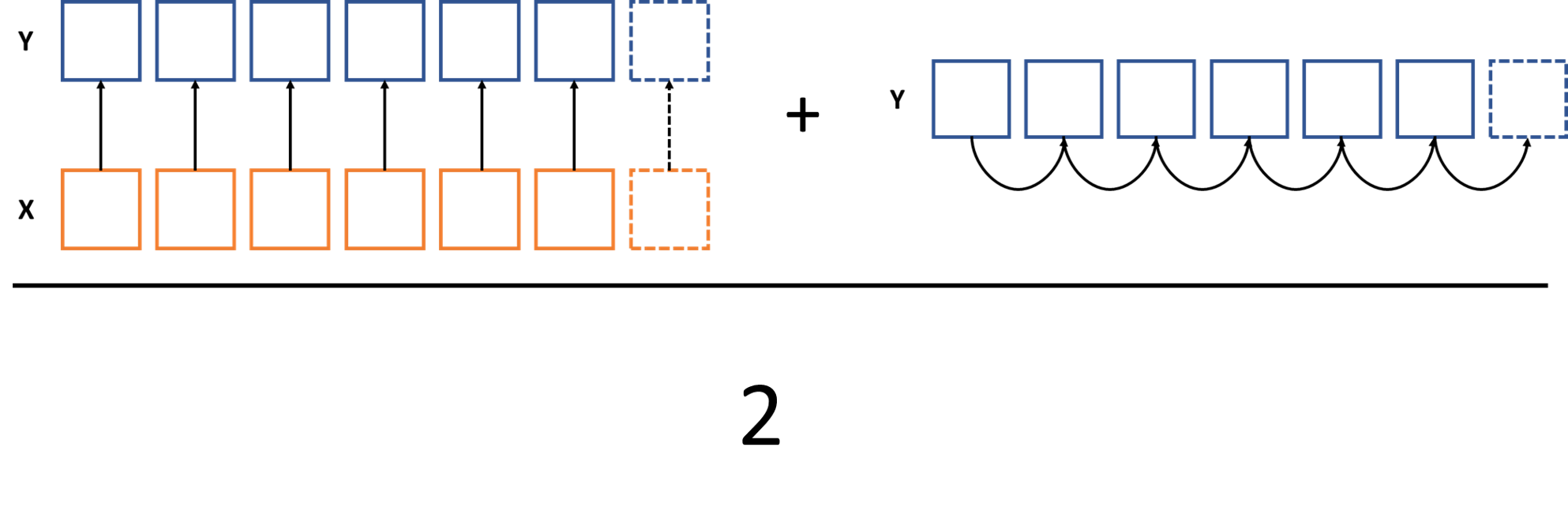
Time Series for Demand

M_hi_model_arima <- auto.arima(M_hi)
summary(M_hi_model_arima)

Series: M_hi 
ARIMA(4,0,2) with non-zero mean 

Coefficients:
          ar1     ar2      ar3      ar4     ma1     ma2      mean
      -0.1332  0.1546  -0.2638  -0.2063  0.7622  0.0492  458.7097
s.e.   0.4729  0.4150   0.2542   0.1399  0.4807  0.3204    5.7040

sigma^2 estimated as 3323:  log likelihood=-839.66
AIC=1695.33   AICc=1696.32   BIC=1719.62

dates_valid <- seq(as.Date("2017-01-01"), length = 22, 
                                          by = "weeks")
for_M_hi_xts <- xts(for_M_hi$mean, order.by = dates_valid)

MAE <- mean(abs(for_M_hi_xts - M_hi_v))
MAPE <- 100*mean(abs((for_M_hi_xts - M_hi_v)/M_hi_v))

print(MAE)

[1] 71.43732

print(MAPE)

[1] 16.29178

Ensembling Example

for_M_hi_en <- 0.5*(for_M_hi_xts + pred_M_hi_xts)

MAE <- mean(abs(for_M_hi_en - M_hi_v))
MAPE <- 100*mean(abs((for_M_hi_en - M_hi_v)/M_hi_v))

print(MAE)

[1] 64.12486

print(MAPE)

[1] 14.38913

Let's practice!

Forecasting Product Demand in R