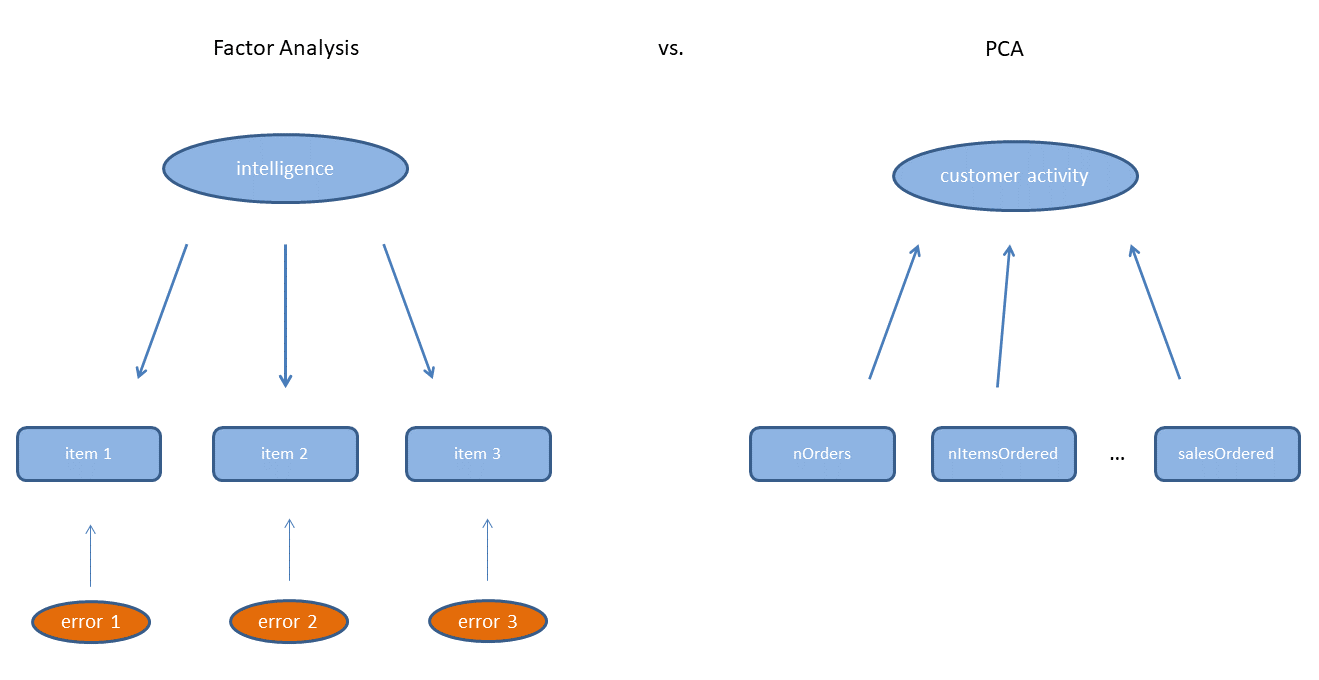
Principal components in a regression analysis

Machine Learning for Marketing Analytics in R

Verena Pflieger

Data Scientist at INWT Statistics

PC in regression analysis I

mod1 <- lm(customerSatis ~ ., dataCustomers)

library(car)
vif(mod1)

      nOrders       nItemsOrdered          nItemsSold        salesOrdered 
    29.482287           24.437448           10.390998            5.134720 
    salesSold         returnRatio       shareOwnBrand           shareSale 
     9.685617           23.778800            1.571607            1.178773 
 shareVoucher          crDuration monetaryReturnRatio  meanDaysBetwOrders 
     1.213011            1.757509           10.632243            1.698369 
salesPerOrder        salesPerItem       itemsPerOrder   itemsSoldPerOrder 
     6.563474            4.557981            4.821610           15.949072

# Create dataframe with customer satisfaction and first 6 components
dataCustComponents <- cbind(dataCustomers[, "customerSatis"], 
                            pcaCust$x[,1:6]) %>%
  as.data.frame
mod2 <- lm(customerSatis ~ ., dataCustComponents)
vif(mod2)

PC1 PC2 PC3 PC4 PC5 PC6 
  1   1   1   1   1   1

summary(mod1)$adj.r.squared

0.8678583

summary(mod2)$adj.r.squared

0.7123822

summary(mod2)

Call:
lm(formula = customerSatis ~ ., data = dataCustComponents)
Residuals:
    Min      1Q  Median      3Q     Max 
-3.9279 -0.2411  0.0179  0.2865  1.4972 
Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2.985945   0.014039 212.682  < 2e-16 ***
PC1         -0.175434   0.006704 -26.167  < 2e-16 ***
PC2          0.296659   0.007643  38.815  < 2e-16 ***
PC3         -0.012816   0.010838  -1.182    0.237    
PC4         -0.116651   0.011665 -10.000  < 2e-16 ***
PC5          0.101963   0.012508   8.152 1.09e-15 ***
PC6          0.126677   0.013072   9.691  < 2e-16 ***
- - -
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4415 on 982 degrees of freedom
Multiple R-squared:  0.7141,    Adjusted R-squared:  0.7124 
F-statistic: 408.9 on 6 and 982 DF,  p-value: < 2.2e-16

	Learnings about PCA
You have learned...	to reduce the number of variables without losing too much information
	that variables should be standardized before a PCA
	how to decide on the number of relevant components
	to interpret the selected components

	Learnings from the model
You have learned...	that the original variables can be reduced to 6 components, i.a., customer activity, return behavior and brand awareness
	that using the first six components to explain customer satisfaction causes a decrease in explained variance, but solves the multicollinearity problem

Let's practice!

Machine Learning for Marketing Analytics in R