Parts of a regression

Hierarchical and Mixed Effects Models in R

Richard Erickson

Data Scientist

An intercept

$y = \beta + \epsilon$

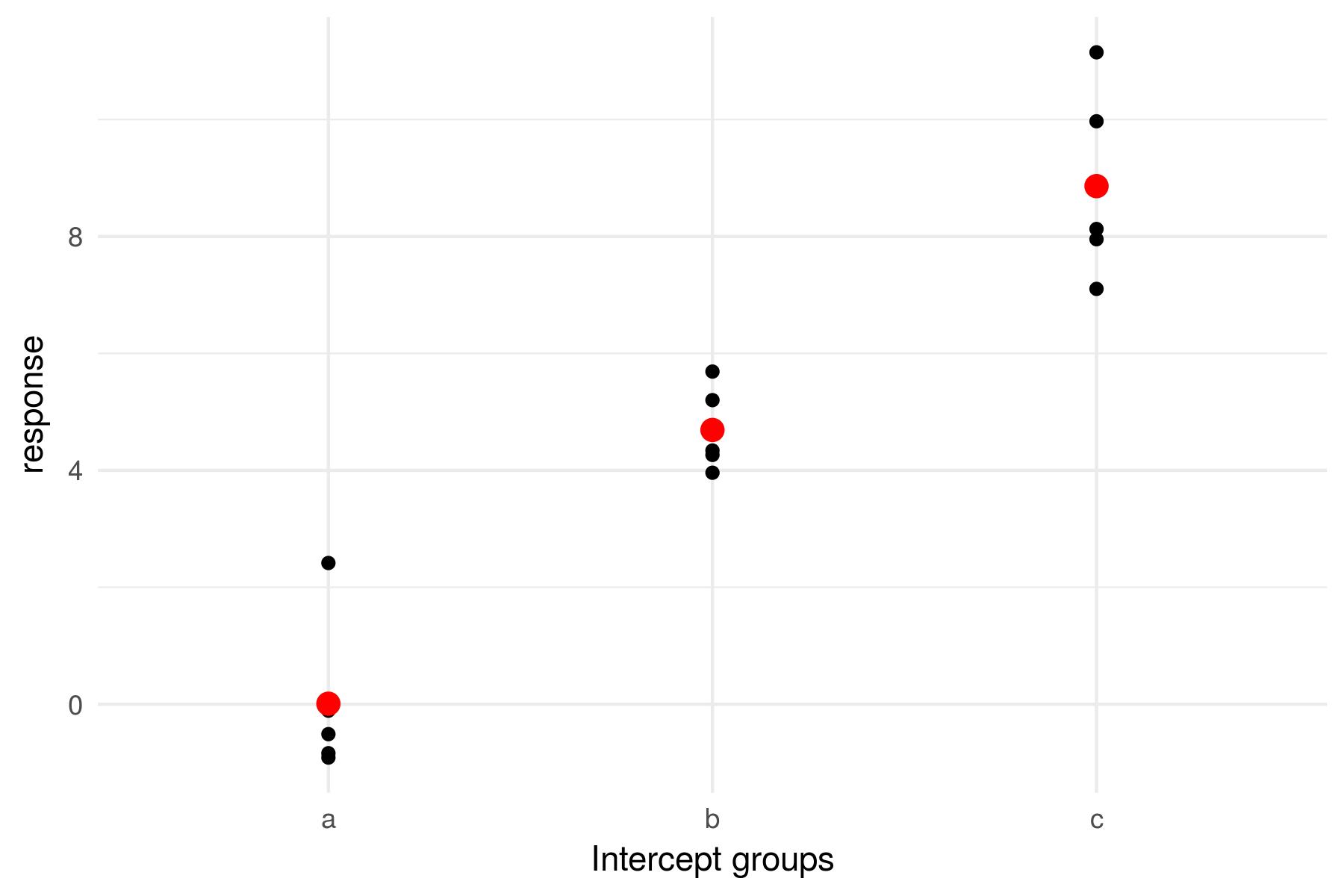
Multiple intercepts

$y = \beta_0 + \beta_2 x_2+ \beta_3 x_3+ \epsilon$

$y = \beta_1 x_1 + \beta_2 x_2+ \beta_3 x_3+ \epsilon$

Picture of multiple intercepts

Linear models in R

lm(formula, data)

lm(y ~ x, data = myData)

anova(lm(y ~ x, data = myData))

A simple linear regression with slopes

$y \sim \beta_0 + \beta_1 x + \epsilon$

Multiple regression

$y \sim \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \ldots + \epsilon$

Multiple regression caveats

Independence of predictor variables
"corrected for..."
Simpson's paradox
Only linear
Interactions may be important

Multiple regression in R tips

lm(y ~ x - 1) estimates an intercept for each x
Numeric versus factors
Scaling parameters and slopes
lm(y ~ x1 + x2 + x1:x2) can be written as lm(y ~ x1 * x2)

Refresher of running and plotting a linear regression in R

reg_model <- lm(response ~ predictor, data = reg_demo)

summary(reg_model)
reg_model
reg_coef_plot <- tidy(reg_model)

ggplot(reg_model, aes(x = predictor, y = response)) +
    geom_point() +
    theme_minimal()  + 
    geom_abline(intercept = reg_model$estimate[1],
                slope = reg_model$estimate[2])

Let's practice!

Hierarchical and Mixed Effects Models in R