The spectrogram - spectral changes to sound over time
Machine Learning for Time Series Data in Python

Chris Holdgraf
Fellow, Berkeley Institute for Data Science
Fourier transforms
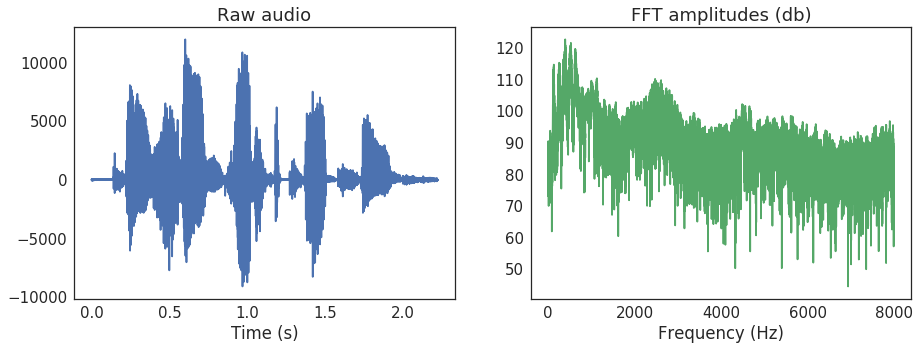
- Timeseries data can be described as a combination of quickly-changing things and slowly-changing things
- At each moment in time, we can describe the relative presence of fast- and slow-moving components
- The simplest way to do this is called a Fourier Transform
- This converts a single timeseries into an array that describes the timeseries as a combination of oscillations
A Fourier Transform (FFT)
Spectrograms: combinations of windows Fourier transforms
- A spectrogram is a collection of windowed Fourier transforms over time
- Similar to how a rolling mean was calculated:
- Choose a window size and shape
- At a timepoint, calculate the FFT for that window
- Slide the window over by one
- Aggregate the results
- Called a Short-Time Fourier Transform (STFT)
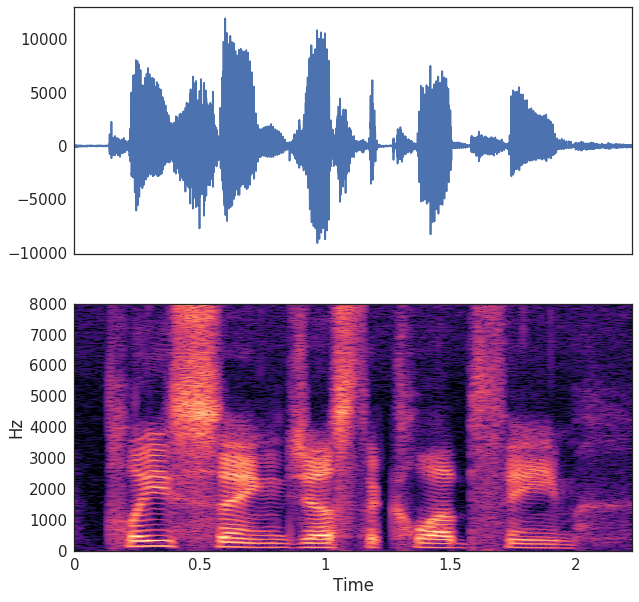
Calculating the STFT
- We can calculate the STFT with
librosa - There are several parameters we can tweak (such as window size)
- For our purposes, we'll convert into decibels which normalizes the average values of all frequencies
- We can then visualize it with the
specshow()function
Calculating the STFT with code
# Import the functions we'll use for the STFT
from librosa.core import stft, amplitude_to_db
from librosa.display import specshow
import matplotlib.pyplot as plt
# Calculate our STFT
HOP_LENGTH = 2**4
SIZE_WINDOW = 2**7
audio_spec = stft(audio, hop_length=HOP_LENGTH, n_fft=SIZE_WINDOW)
# Convert into decibels for visualization
spec_db = amplitude_to_db(audio_spec)
# Visualize
fig, ax = plt.subplots()
specshow(spec_db, sr=sfreq, x_axis='time',
y_axis='hz', hop_length=HOP_LENGTH, ax=ax)
Spectral feature engineering
- Each timeseries has a different spectral pattern.
- We can calculate these spectral patterns by analyzing the spectrogram.
- For example, spectral bandwidth and spectral centroids describe where most of the energy is at each moment in time
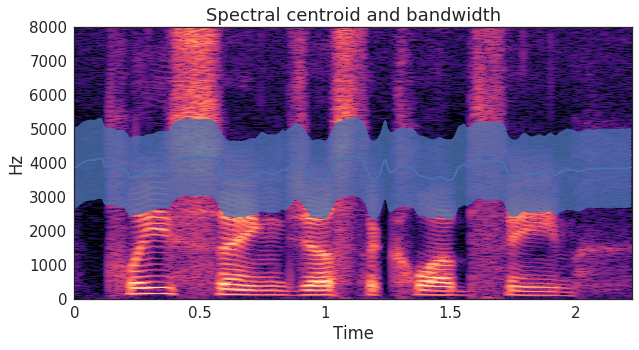
Calculating spectral features
# Calculate the spectral centroid and bandwidth for the spectrogram
bandwidths = lr.feature.spectral_bandwidth(S=spec)[0]
centroids = lr.feature.spectral_centroid(S=spec)[0]
# Display these features on top of the spectrogram
fig, ax = plt.subplots()
specshow(spec, x_axis='time', y_axis='hz', hop_length=HOP_LENGTH, ax=ax)
ax.plot(times_spec, centroids)
ax.fill_between(times_spec, centroids - bandwidths / 2,
centroids + bandwidths / 2, alpha=0.5)
Combining spectral and temporal features in a classifier
centroids_all = []
bandwidths_all = []
for spec in spectrograms:
bandwidths = lr.feature.spectral_bandwidth(S=lr.db_to_amplitude(spec))
centroids = lr.feature.spectral_centroid(S=lr.db_to_amplitude(spec))
# Calculate the mean spectral bandwidth
bandwidths_all.append(np.mean(bandwidths))
# Calculate the mean spectral centroid
centroids_all.append(np.mean(centroids))
# Create our X matrix
X = np.column_stack([means, stds, maxs, tempo_mean,
tempo_max, tempo_std, bandwidths_all, centroids_all])
Let's practice!
Machine Learning for Time Series Data in Python

