Cross-validating timeseries data

Machine Learning for Time Series Data in Python

Chris Holdgraf

Fellow, Berkeley Institute for Data Science

Cross validation with scikit-learn

# Iterating over the "split" method yields train/test indices
for tr, tt in cv.split(X, y):
    model.fit(X[tr], y[tr])
    model.score(X[tt], y[tt])

Cross validation types: KFold

KFold cross-validation splits your data into multiple "folds" of equal size

It is one of the most common cross-validation routines

  from sklearn.model_selection import KFold
  cv = KFold(n_splits=5)
  for tr, tt in cv.split(X, y):
      ...

Visualizing model predictions

fig, axs = plt.subplots(2, 1)

# Plot the indices chosen for validation on each loop
axs[0].scatter(tt, [0] * len(tt), marker='_', s=2, lw=40)
axs[0].set(ylim=[-.1, .1], title='Test set indices (color=CV loop)', 
           xlabel='Index of raw data')

# Plot the model predictions on each iteration
axs[1].plot(model.predict(X[tt]))
axs[1].set(title='Test set predictions on each CV loop', 
           xlabel='Prediction index')

Visualizing KFold CV behavior

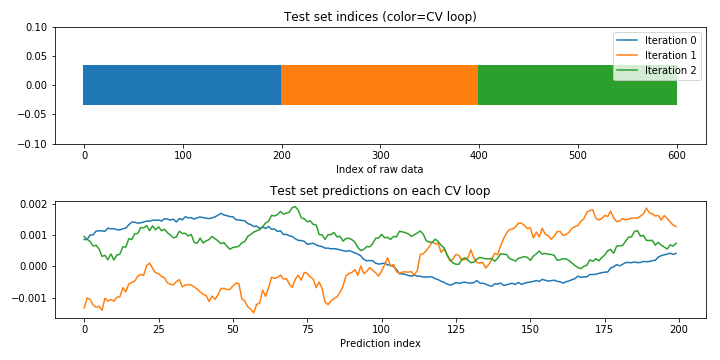
A note on shuffling your data

Many CV iterators let you shuffle data as a part of the cross-validation process.
This only works if the data is i.i.d., which timeseries usually is not.

You should not shuffle your data when making predictions with timeseries.

  from sklearn.model_selection import ShuffleSplit

  cv = ShuffleSplit(n_splits=3)
  for tr, tt in cv.split(X, y):
      ...

Visualizing shuffled CV behavior

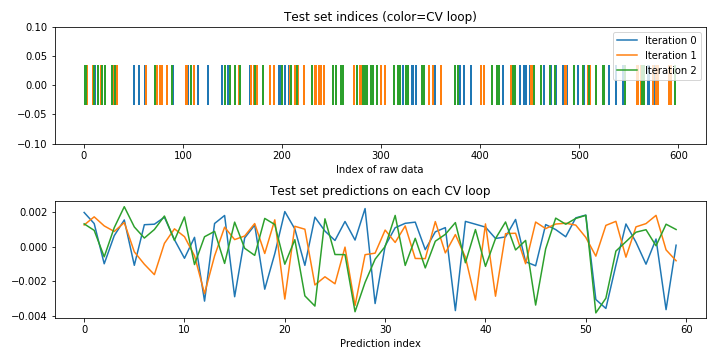
Using the time series CV iterator

Thus far, we've broken the linear passage of time in the cross validation
However, you generally should not use datapoints in the future to predict data in the past
One approach: Always use training data from the past to predict the future

Visualizing time series cross validation iterators

# Import and initialize the cross-validation iterator
from sklearn.model_selection import TimeSeriesSplit
cv = TimeSeriesSplit(n_splits=10)

fig, ax = plt.subplots(figsize=(10, 5))
for ii, (tr, tt) in enumerate(cv.split(X, y)):
    # Plot training and test indices
    l1 = ax.scatter(tr, [ii] * len(tr), c=[plt.cm.coolwarm(.1)], 
                    marker='_', lw=6)
    l2 = ax.scatter(tt, [ii] * len(tt), c=[plt.cm.coolwarm(.9)], 
                    marker='_', lw=6)
    ax.set(ylim=[10, -1], title='TimeSeriesSplit behavior', 
           xlabel='data index', ylabel='CV iteration')
    ax.legend([l1, l2], ['Training', 'Validation'])

Visualizing the TimeSeriesSplit cross validation iterator

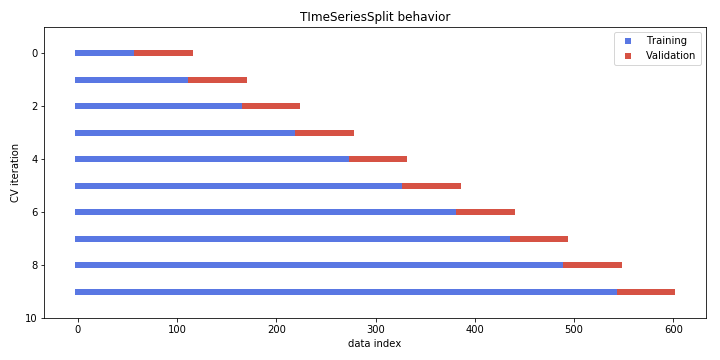
Custom scoring functions in scikit-learn

def myfunction(estimator, X, y):
    y_pred = estimator.predict(X)
    my_custom_score = my_custom_function(y_pred, y)
    return my_custom_score

A custom correlation function for scikit-learn

def my_pearsonr(est, X, y):
    # Generate predictions and convert to a vector 
    y_pred = est.predict(X).squeeze()

    # Use the numpy "corrcoef" function to calculate a correlation matrix
    my_corrcoef_matrix = np.corrcoef(y_pred, y.squeeze())

    # Return a single correlation value from the matrix
    my_corrcoef = my_corrcoef[1, 0]
    return my_corrcoef

Let's practice!

Machine Learning for Time Series Data in Python