Understanding statistical significance

Customer Analytics and A/B Testing in Python

Ryan Grossman

Data Scientist, EDO

Revisiting statistical significance

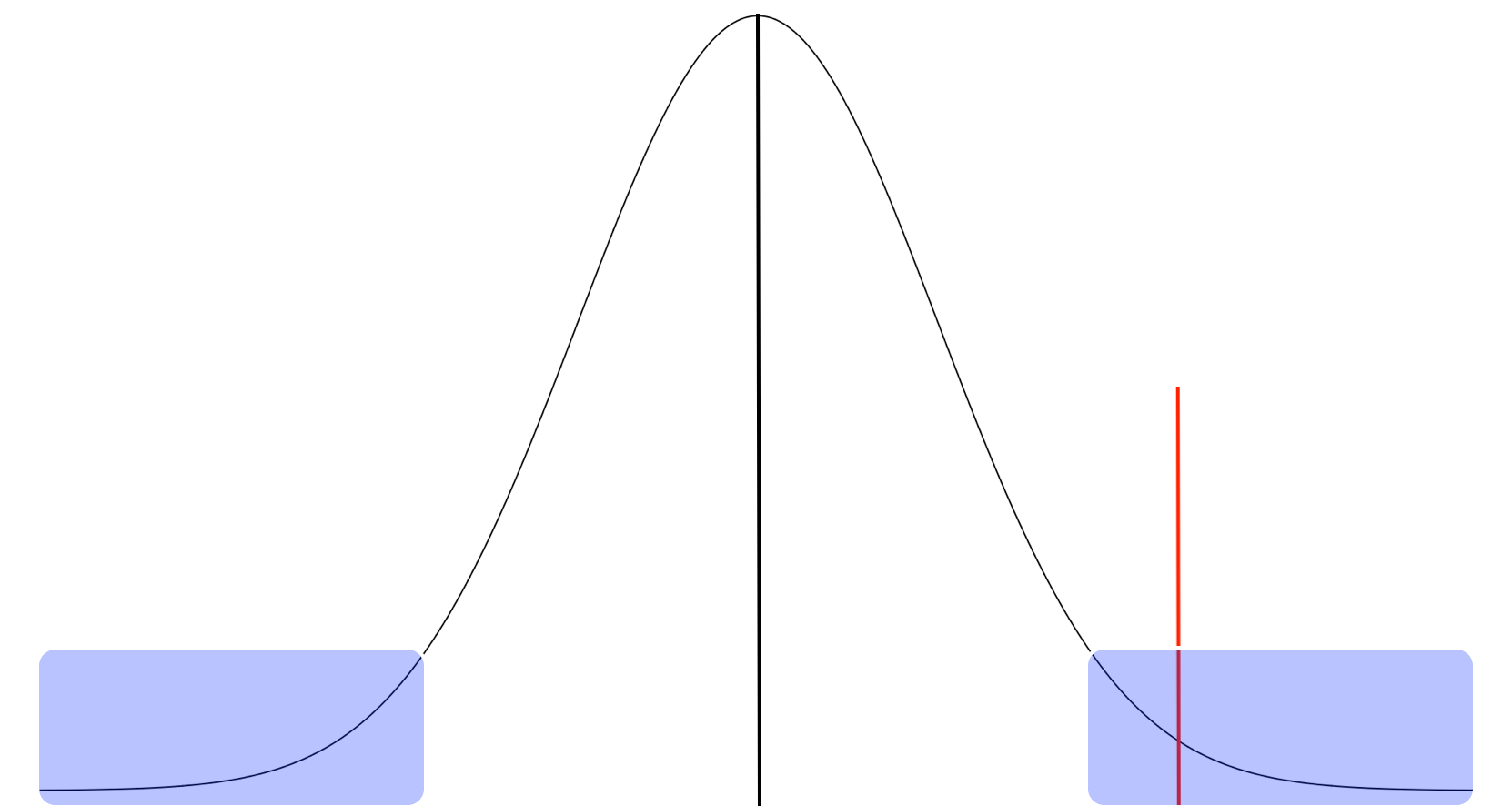
Distribution of expected difference between control and test groups _if_ the Null Hypothesis true
Red line: The observed difference in conversion rates from our test
p-value: Probability of being as or more extreme than the red line on either side of the distribution

alt

p-value Function

# calculate the p-value from our 
# group conversion rates and  group sizes
def get_pvalue(con_conv, test_conv,con_size,  test_size,):  
    lift =  - abs(test_conv - con_conv)
    scale_one = con_conv * (1 - con_conv) * (1 / con_size)
    scale_two = test_conv * (1 - test_conv) * (1 / test_size)
    scale_val = (scale_one + scale_two)**0.5
    p_value = 2 * stats.norm.cdf(lift, loc = 0, scale = scale_val )

    return p_value

Calculating our p-value

Observe a small p-value and statistically significant results
Achieved lift is relatively large

# previously calculated quantities 
con_conv  = 0.034351 # control group conversion rate
test_conv = 0.041984 # test group conversion rate
con_size  = 48236 # control group size 
test_size = 49867 # test group size


# calculate the test p-value
p_value = get_pvalue(_conv, con_size, test_size)
print(p_value)

4.2572974855869089e-10

Finding the power of our test

# Calculate our test's power 
get_power(test_size, con_conv, test_conv, 0.95)

0.99999259413722819

What is a confidence interval

Range of values for our estimation rather than single number
Provides context for our estimation process
Series of repeated experiments...
- the calculated intervals will contain the true parameter X% of the time
The true conversion rate is a fixed quantity, our estimation and the interval are variable

Confidence interval calculation

Confidence Interval Formula $$\mu \pm \Phi\left(\alpha + \frac{1 - \alpha}{2}\right) \times \sigma$$

Estimated parameter (difference in conversion rates) follows Normal Distribution
Can estimate the:
- standard deviation ($\sigma$) and...
- mean ($\mu$) of this distribution
$\alpha$: Desired confidence interval width
Bounds containing X% of the probability around the mean (e.g. 95%) of that distribution

Confidence interval function

# Calculate the confidence interval 
from scipy import stats
def get_ci(test_conv, con_conv, 
    test_size, con_size, ci):

    sd = ((test_conv * (1 - test_conv)) / test_size +
        (con_conv * (1 - con_conv)) / con_size)**0.5
    lift = test_conv - con_conv

    val = stats.norm.isf((1 - ci) / 2)
    lwr_bnd = lift - val * sd
      upr_bnd = lift + val * sd

    return((lwr_bnd, upr_bnd))

Calculating confidence intervals

test_conv: test group conversion rate
con_conv: control group conversion rate
test_size: test group observations
con_size: control group observations

# Calcualte the conversion rate
get_ci(
    test_conv, con_conv, 
    test_size, con_size, 
    0.95
)

(0.00523, 0.0100)

Provides additional context about our results

Next steps

Adding context to our test results
Communicating the data through visualizations

Let's practice!

Customer Analytics and A/B Testing in Python