Interactions with different scales: Tensors

Nonlinear Modeling with Generalized Additive Models (GAMs) in R

Noam Ross

Senior Research Scientist, EcoHealth Alliance

Interactions with one smoothing parameter

$$\LARGE y = s(x_1, x_2)$$

$$\LARGE \text{ with smoothing parameter } \lambda$$

Variables with different scales or wiggliness

Numeric terms from meuse on different scales:

        x      y  elev    om
 1 181072 333611  7.91   13.6
 2 181025 333558  6.98   14  
 3 181165 333537  7.8    13  
 4 181298 333484  7.66   8  
 5 181307 333330  7.48   8.7
 6 181390 333260  7.79   7.8
 7 181165 333370  8.22   9.2
 8 181027 333363  8.49   9.5
 9 181060 333231  8.67   10.6
10 181232 333168  9.05   6.3

Tensor smooths

$$\LARGE y = te(x_1, x_2)$$

$$\Large \text{ with smoothing parameters } \lambda_1, \lambda_2$$

gam(y ~ te(x1, x2), data = data, 
                    method = "REML")

gam(y ~ te(x1, x2, k = c(10, 20)), data = data, 
                                   method = "REML")

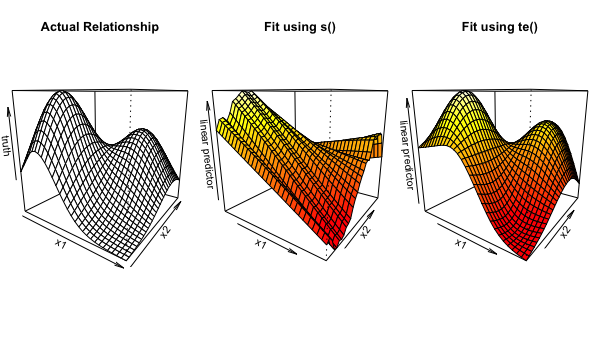
Tensor interactions

$$\LARGE y = s(x_1) + s(x_2) + ti(x_1, x_2)$$

$$\LARGE \text{ with smoothing parameters } $$ $$\LARGE \lambda_1, \lambda_2, \lambda_3, \lambda_4$$

gam(y ~ s(x1) + s(x2) + ti(x1, x2), data = data, 
                                    method = "REML")

Family: gaussian 
Link function: identity 
Formula:
y ~ s(x1) + s(x2) + ti(x1, x2)

Parametric coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.318698   0.008697   36.65   <2e-16 ***
 ---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
            edf Ref.df     F  p-value    
te(x1)      4.93  6.009 23.16  < 2e-16 ***    # Separate terms for 
te(x2)      3.42  4.242 10.35 2.75e-08 ***    # each variable and
ti(x1,x2) 10.15 12.763 16.08  < 2e-16 ***     # the interaction
 ---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =  0.444   Deviance explained = 46.5%
-REML = -85.566  Scale est. = 0.037067  n = 500

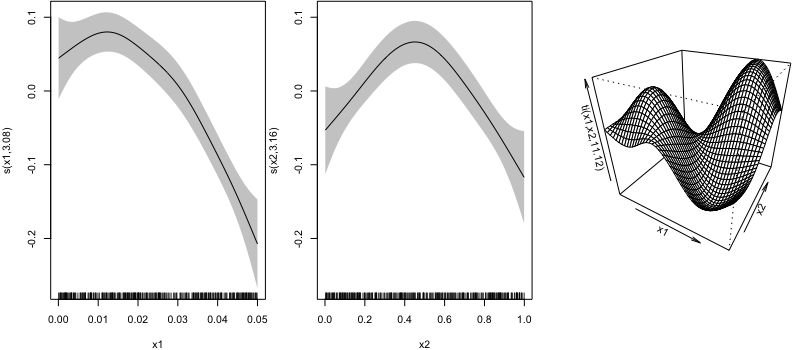
Example: tensor interactions

gam(y ~ s(x1) + s(x2) + ti(x1, x2), data = data, 
                                    method = "REML")

Let's practice!

Nonlinear Modeling with Generalized Additive Models (GAMs) in R