Posterior prediction

Bayesian Modeling with RJAGS

Alicia Johnson

Associate Professor, Macalester College

Posterior trend

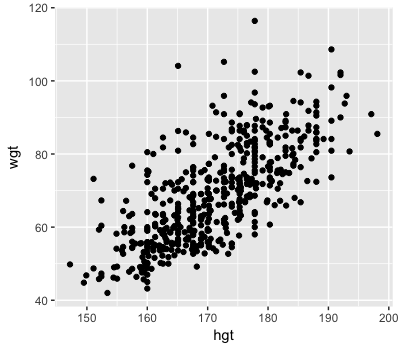
$Y \sim N(m, s^2)$
$m = a + b X$

Posterior trend

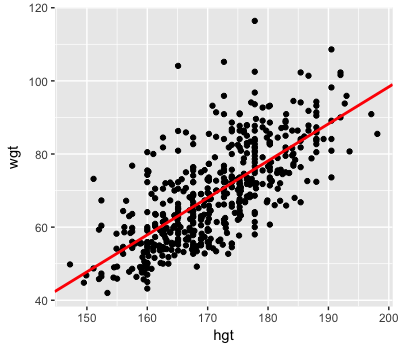
$Y \sim N(m, s^2)$
$m = a + b X$

Posterior mean trend
$m = -104.038 + 1.012 X$

Posterior trend when height = 180 cm

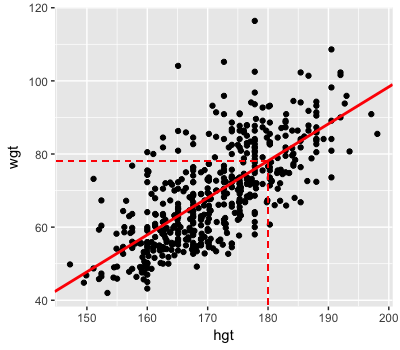
$Y \sim N(m, s^2)$
$m = a + b X$

Posterior mean trend
$m = -104.038 + 1.012 X$

-104.038 + 1.012 * 180

78.122

Estimating posterior trend when height = 180 cm

-104.038 + 1.012 * 180

78.122

head(weight_chains)

          a        b        s
1 -113.9029 1.072505 8.772007
2 -115.0644 1.077914 8.986393
3 -114.6958 1.077130 9.679812
4 -115.0568 1.072668 8.814403
5 -114.0782 1.071775 8.895299
6 -114.3271 1.069477 9.016185

-104.038 + 1.012 * 180

78.122

weight_chains <- weight_chains  %>% mutate(m_180 = a + b * 180)
head(weight_chains)

          a        b        s      m_180
1 -113.9029 1.072505 8.772007   79.14803
2 -115.0644 1.077914 8.986393   78.96014
3 -114.6958 1.077130 9.679812   79.18771
4 -115.0568 1.072668 8.814403   78.02352
5 -114.0782 1.071775 8.895299   78.84138
6 -114.3271 1.069477 9.016185   78.17877

-113.9029 + 1.072505 * 180

79.148

Posterior distribution of trend

-104.038 + 1.012 * 180

78.122

head(weight_chains$m_180)

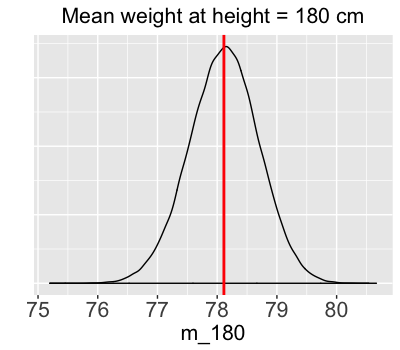
Credible interval for posterior trend

-104.038 + 1.012 * 180

78.122

head(weight_chains$m_180)

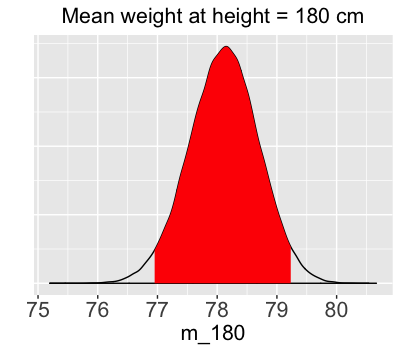
quantile(weight_chains$m_180, 
    c(0.025, 0.975))

    2.5%    97.5% 
76.95054 79.23619

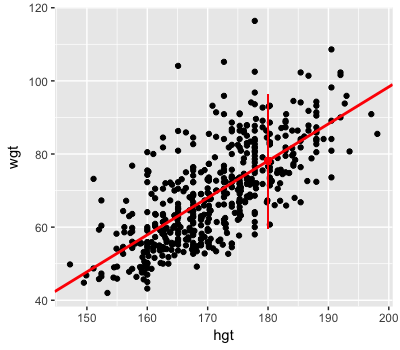
Visualizing posterior trend

-104.038 + 1.012 * 180

78.122

head(weight_chains$m_180)

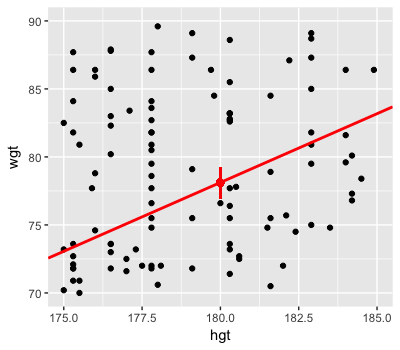
quantile(weight_chains$m_180, 
    c(0.025, 0.975))

    2.5%    97.5% 
76.95054 79.23619

Posterior trend vs posterior prediction

Posterior mean weight (or trend) among all 180 cm tall adults

-104.038 + 1.012 * 180

78.122

Posterior predicted weight of a specific 180 cm tall adult

-104.038 + 1.012 * 180

78.122

$Y \sim N(m_{180}, s^2)$ $m_{180} = a + b * 180$

head(weight_chains, 3)

          a        b        s      m_180
1 -113.9029 1.072505 8.772007   79.14803
2 -115.0644 1.077914 8.986393   78.96014
3 -114.6958 1.077130 9.679812   79.18771

set.seed(2000)
rnorm(n = 1, mean = 79.14803, sd = 8.772007)

71.65811

rnorm(n = 1, mean = 78.96014, sd = 8.986393)

75.78894

rnorm(n = 1, mean = 79.18771, sd = 9.679812)

87.80419

Posterior predictive distribution

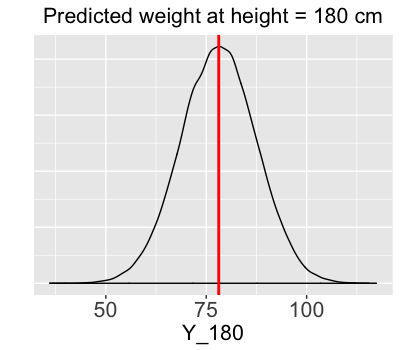
Posterior prediction interval

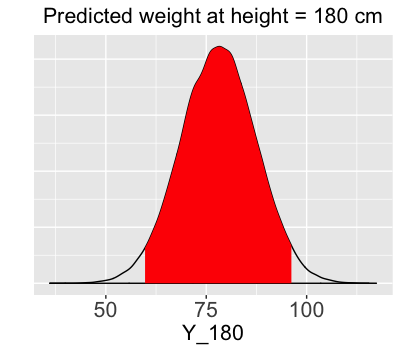
Let's practice!

Bayesian Modeling with RJAGS