Markov chain diagnostics & reproducibility
Bayesian Modeling with RJAGS

Alicia Johnson
Associate Professor, Macalester College
Markov chain output
Questions to consider
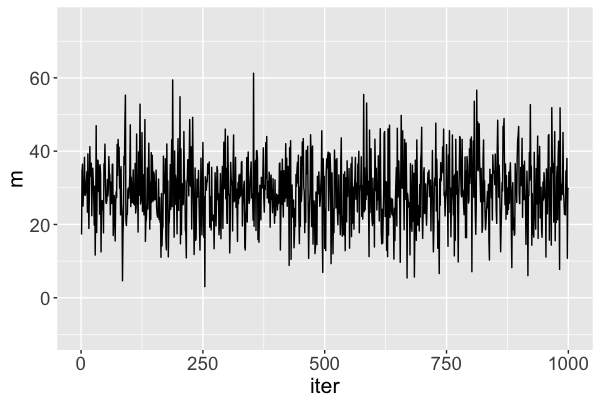
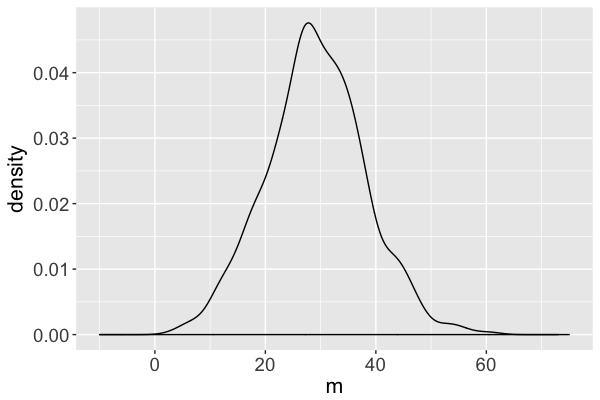
What does a "good" Markov chain look like?
How accurate is the Markov chain approximation of the posterior?
For how many iterations should we run the Markov chain?
Diagnostic: trace plots

Diagnostic: trace plots
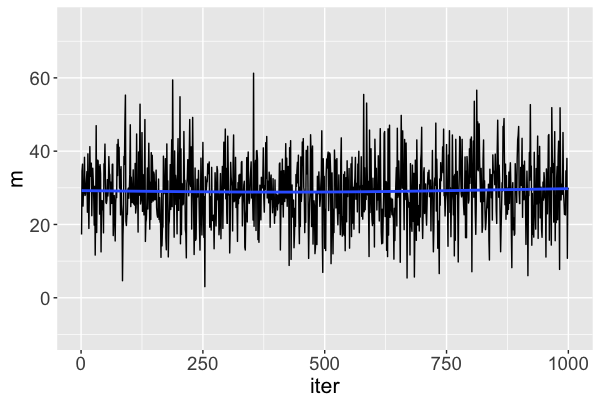
Good: stability!
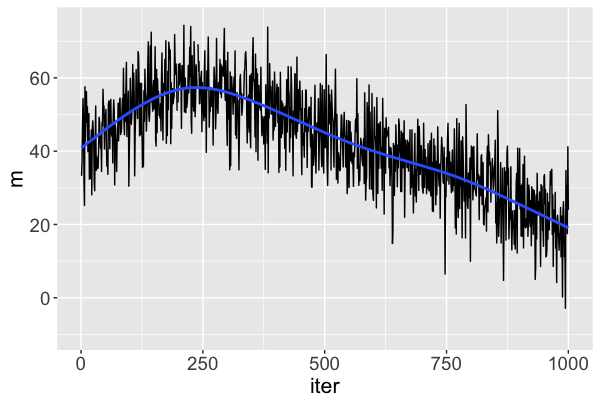
Bad: instability
Diagnostic: multiple chains
# COMPILE the model
sleep_jags <- jags.model(..., n.chains = 1)
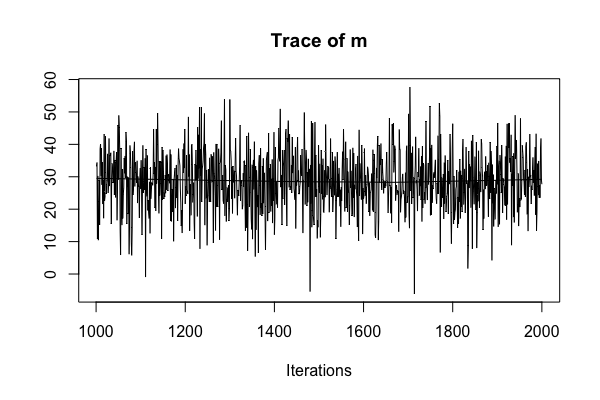
Diagnostic: multiple chains
# COMPILE the model
sleep_jags <- jags.model(..., n.chains = 2)
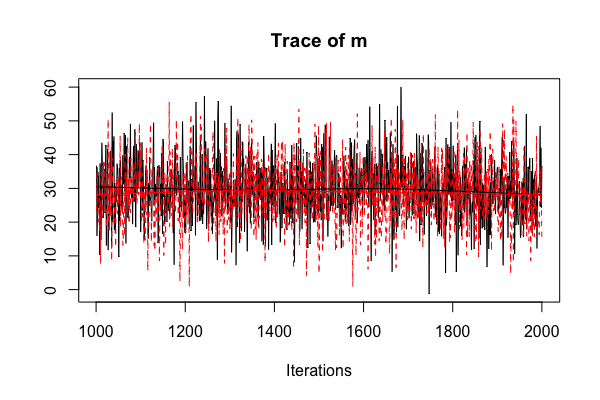
Diagnostic: multiple chains
# COMPILE the model
sleep_jags <- jags.model(..., n.chains = 4)
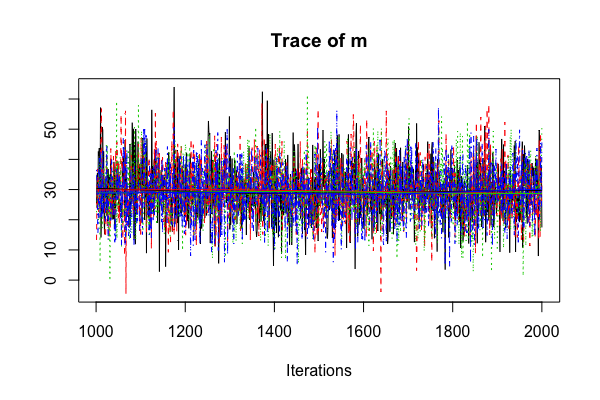
Diagnostic: multiple chains
# COMPILE the model
sleep_jags <- jags.model(..., n.chains = 4)

summary(sleep_sim)
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
m 29.10 8.968 0.2836 0.2820
s 40.07 7.887 0.2494 0.4227
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
m 11.42 23.27 28.85 34.76 46.76
s 28.31 34.65 38.93 43.91 57.56
Estimate of the posterior mean of $m$ = 29.10 ms
(Naive) standard error of this estimate = 0.2836 ms
SD/ $\sqrt{\text{number of iterations}}$
Diagnostic: standard error
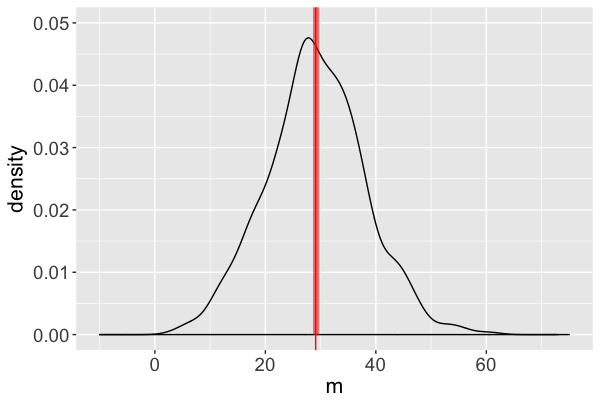
Estimated mean = 29.10 ms
(Naive) standard error = 0.2836 ms
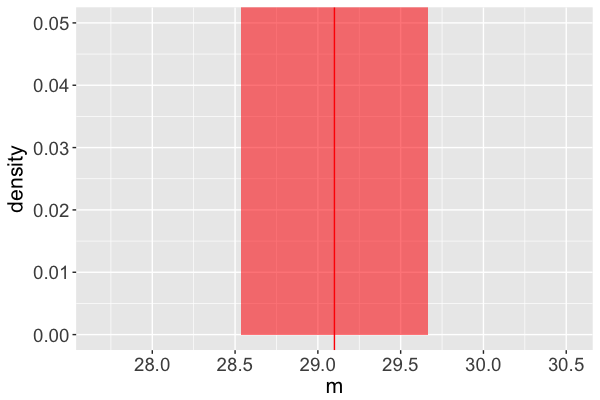
- $29.10 \pm 2*0.2836$
Markov chain work flow
Define, compile, simulate the model
Examine the following diagnostics:
- Trace plots
- Multiple chain output
- Standard errors
Finalize the simulation
Finalizing the Markov chain: Reproducibility
sleep_jags <- jags.model(textConnection(sleep_model),
data = list(Y = sleep_study$diff_3),
inits = list(.RNG.name = "base::Wichmann-Hill",
.RNG.seed = 1989))
Let's practice!
Bayesian Modeling with RJAGS

