Posterior estimation & inference

Bayesian Modeling with RJAGS

Alicia Johnson

Associate Professor, Macalester College

Bayesian regression model

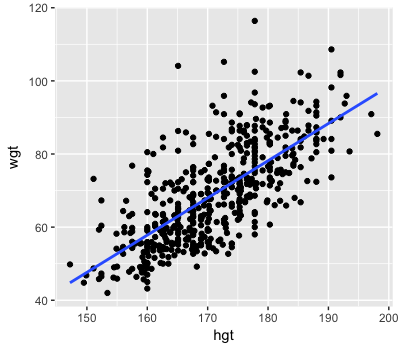
$Y_i$ = weight of adult $i$ (kg)
$X_i$ = height of adult $i$ (cm)

$\;$

Model

$Y_i \sim N(m_i, s^2)$
$m_i = a + b X_i$

$a \sim N(0, 200^2)$
$b \sim N(1, 0.5^2)$
$s \sim \text{Unif}(0, 20)$

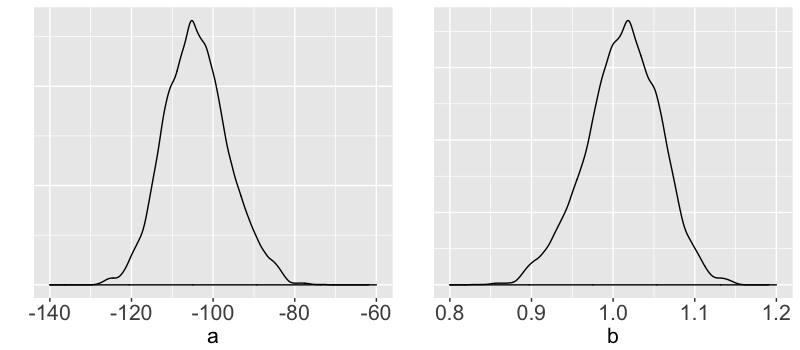
Posterior point estimation

summary(weight_sim_big)

1. Empirical mean and standard deviation for each variable,
   plus standard error of the mean:
      Mean      SD  Naive SE Time-series SE
a -104.038 7.85296 0.0248332       0.661515
b    1.012 0.04581 0.0001449       0.003849
s    9.331 0.29495 0.0009327       0.001216

2. Quantiles for each variable:
       2.5%       25%      50%     75%   97.5%
a -118.6843 -109.5171 -104.365 -99.036 -87.470
b    0.9152    0.9828    1.014   1.044   1.098
s    8.7764    9.1284    9.322   9.524   9.933

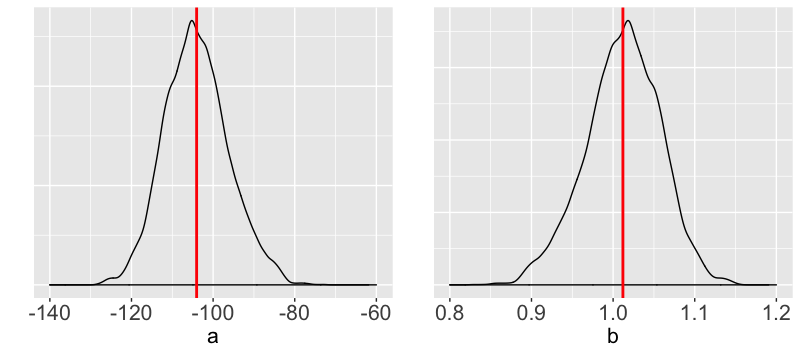
Posterior mean of $a$ $\approx$ -104.038

Posterior mean of $b$ $\approx$ 1.012

Posterior point estimation

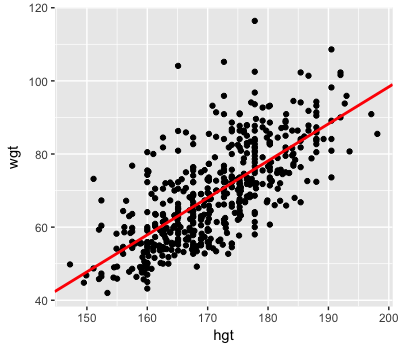
Posterior mean trend:

$m_i = -104.038 + 1.012 X_i$

Markov chain output:

head(weight_chains)

             a        b        s
[1,] -113.9029 1.072505 8.772007
[2,] -115.0644 1.077914 8.986393
[3,] -114.6958 1.077130 9.679812
[4,] -115.0568 1.072668 8.814403
[5,] -114.0782 1.071775 8.895299
[6,] -114.3271 1.069477 9.016185

Posterior uncertainty

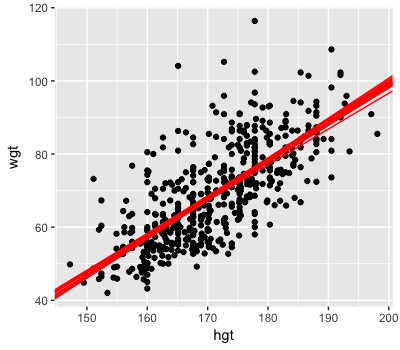
Posterior mean trend:

$m_i = -104.038 + 1.012 X_i$

Markov chain output:

head(weight_chains)

             a        b        s
[1,] -113.9029 1.072505 8.772007
[2,] -115.0644 1.077914 8.986393
[3,] -114.6958 1.077130 9.679812
[4,] -115.0568 1.072668 8.814403
[5,] -114.0782 1.071775 8.895299
[6,] -114.3271 1.069477 9.016185

Posterior credible intervals

summary(weight_sim_big)

1. Empirical mean and standard deviation for each variable,
   plus standard error of the mean:
      Mean      SD  Naive SE Time-series SE
a -104.038 7.85296 0.0248332       0.661515
b    1.012 0.04581 0.0001449       0.003849
s    9.331 0.29495 0.0009327       0.001216

2. Quantiles for each variable:
       2.5%       25%      50%     75%   97.5%
a -118.6843 -109.5171 -104.365 -99.036 -87.470
b    0.9152    0.9828    1.014   1.044   1.098
s    8.7764    9.1284    9.322   9.524   9.933

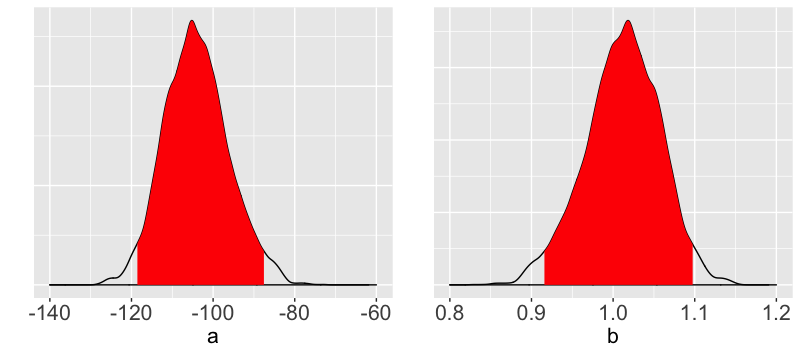
95% posterior credible interval for $a$: (-118.6843, -87.470)

95% posterior credible interval for $b$: (0.9152, 1.098)

Posterior credible intervals

Interpretation

In light of our priors & observed data, there's a 95% (posterior) chance that $b$ is between 0.9152 & 1.098 kg/cm.

Posterior probabilities

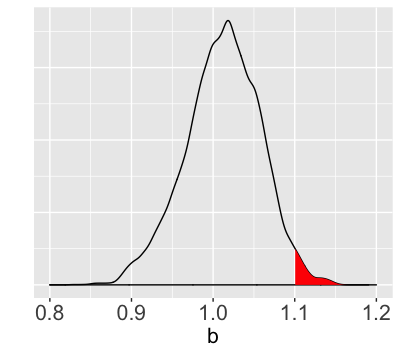
table(weight_chains$b > 1.1)

FALSE  TRUE 
97835  2165

mean(weight_chains$b > 1.1)

0.02165

Interpretation:
There's a 2.165% posterior chance that $b$ exceeds 1.1 kg/cm.

Let's practice!

Bayesian Modeling with RJAGS