Poisson regression

Bayesian Modeling with RJAGS

Alicia Johnson

Associate Professor, Macalester College

Normal likelihood structure

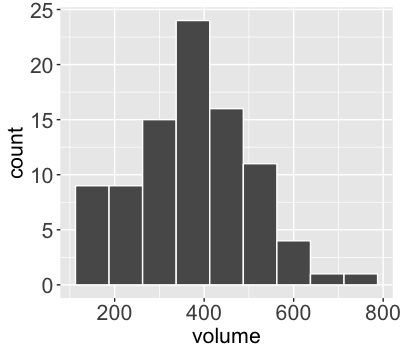
$Y$ = volume (# of users) on a given day
$Y \sim N(m, s^2)$

Technically...

The Normal model assumes $Y$ has a continuous scale and can be negative.
But $Y$ is a discrete count and cannot be negative.

The Poisson model

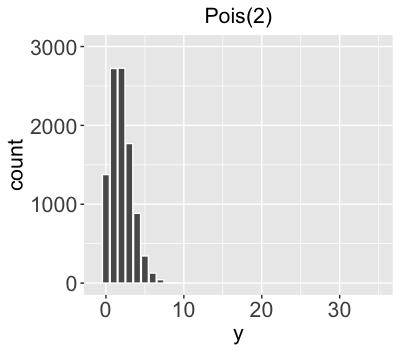
$Y$ = volume (# of users) on a given day
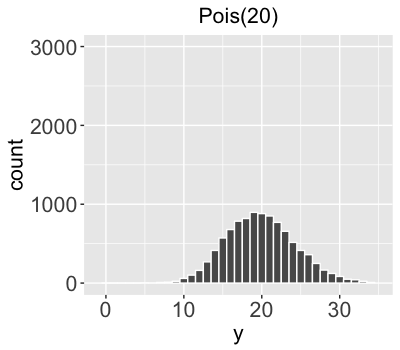
$Y \sim \text{Pois}(l)$

$Y$ is the # of independent events that occur in a fixed interval (0, 1, 2,...).
Rate parameter $l$ represents the typical # of events per time interval
($l > 0$).

The Poisson model

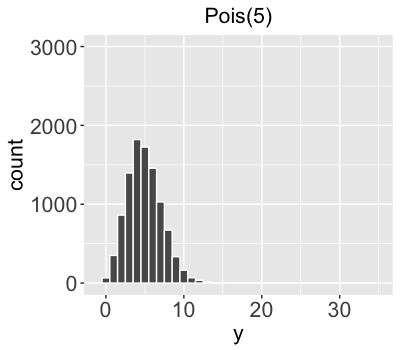
$Y$ = volume (# of users) on a given day
$Y \sim \text{Pois}(l)$

$Y$ is the # of independent events that occur in a fixed interval (0, 1, 2,...).
Rate parameter $l$ represents the typical # of events per time interval
($l > 0$).

The Poisson model

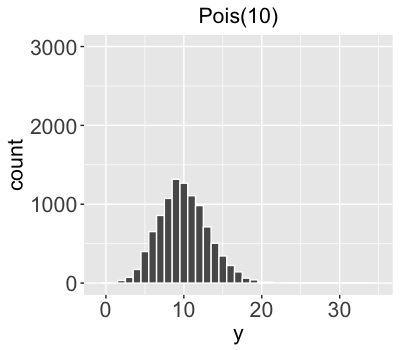
$Y$ = volume (# of users) on a given day
$Y \sim \text{Pois}(l)$

$Y$ is the # of independent events that occur in a fixed interval (0, 1, 2,...).
Rate parameter $l$ represents the typical # of events per time interval
($l > 0$).

The Poisson model

$Y$ = volume (# of users) on a given day
$Y \sim \text{Pois}(l)$

$Y$ is the # of independent events that occur in a fixed interval (0, 1, 2,...).
Rate parameter $l$ represents the typical # of events per time interval
($l > 0$).

Poisson regression

$Y_i \sim \text{Pois}(l_i)$ where $l_i > 0$

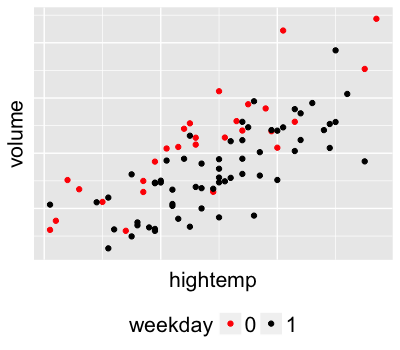
Poisson regression

$Y_i \sim \text{Pois}(l_i)$ where $l_i > 0$

$l_i = a + b X_i + c Z_i$

$\;$

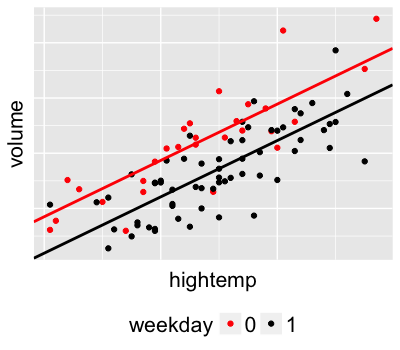
Poisson regression

$Y_i \sim \text{Pois}(l_i)$ where $l_i > 0$

$l_i = a + b X_i + c Z_i$

$\;$

A problem:
Linking $l_i$ directly to the linear model assumes $l_i$ can be negative.

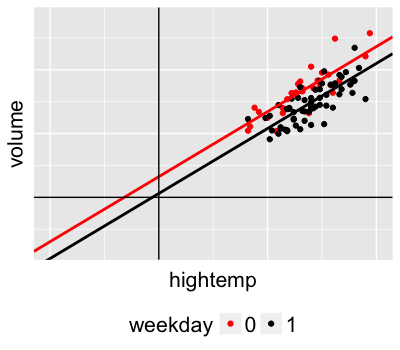
Poisson regression

$Y_i \sim \text{Pois}(l_i)$ where $l_i > 0$

$log(l_i) = a + b X_i + c Z_i$

$\;$

A solution:
Use a log link function to link $l_i$ to the linear model. In turn:

$$l_i = e^{a + b X_i + c Z_i}$$

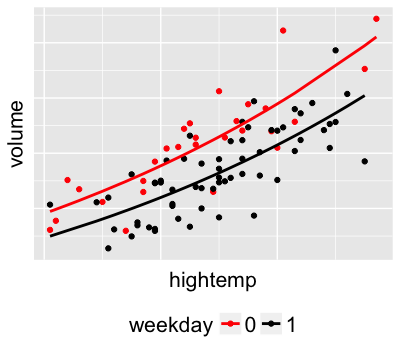
Poisson regression

$Y_i \sim \text{Pois}(l_i)$ where $l_i > 0$

$log(l_i) = a + b X_i + c Z_i$

$\;$

A solution:
Use a log link function to link $l_i$ to the linear model. In turn:

$$l_i = e^{a + b X_i + c Z_i}$$

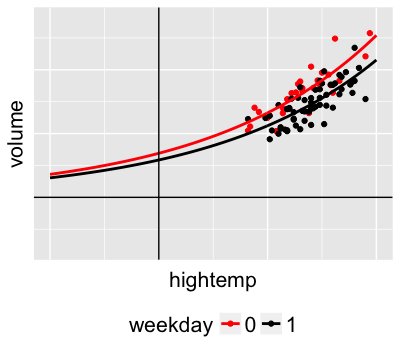
Poisson regression in RJAGS

$Y_i \sim \text{Pois}(l_i)$
$log(l_i) = a + b X_i + c Z_i$
$a \sim N(0, 200^2)$
$b \sim N(0, 2^2)$
$c \sim N(0, 2^2)$

poisson_model <- "model{
  # Likelihood model for Y[i]





  # Prior models for a, b, c




}"

Poisson regression in RJAGS

$Y_i \sim \text{Pois}(l_i)$
$log(l_i) = a + b X_i + c Z_i$
$a \sim N(0, 200^2)$
$b \sim N(0, 2^2)$
$c \sim N(0, 2^2)$

poisson_model <- "model{
  # Likelihood model for Y[i]





  # Prior models for a, b, c
  a ~ dnorm(0, 200^(-2))
  b[1] <- 0
  b[2] ~ dnorm(0, 2^(-2))
  c ~ dnorm(0, 2^(-2))
}"

Poisson regression in RJAGS

$Y_i \sim \text{Pois}(l_i)$
$log(l_i) = a + b X_i + c Z_i$
$a \sim N(0, 200^2)$
$b \sim N(0, 2^2)$
$c \sim N(0, 2^2)$

poisson_model <- "model{
  # Likelihood model for Y[i]
  for(i in 1:length(Y)) {
   Y[i] ~ dpois(l[i])

  }

  # Prior models for a, b, c
  a ~ dnorm(0, 200^(-2))
  b[1] <- 0
  b[2] ~ dnorm(0, 2^(-2))
  c ~ dnorm(0, 2^(-2))
}"

Poisson regression in RJAGS

$Y_i \sim \text{Pois}(l_i)$
$log(l_i) = a + b X_i + c Z_i$
$a \sim N(0, 200^2)$
$b \sim N(0, 2^2)$
$c \sim N(0, 2^2)$

poisson_model <- "model{
  # Likelihood model for Y[i]
  for(i in 1:length(Y)) {
   Y[i] ~ dpois(l[i])
   log(l[i]) <- a + b[X[i]] + c*Z[i]
  }

  # Prior models for a, b, c
  a ~ dnorm(0, 200^(-2))
  b[1] <- 0
  b[2] ~ dnorm(0, 2^(-2))
  c ~ dnorm(0, 2^(-2))
}"

Caveats

$Y \sim \text{Pois}(l_i)$

Assumption: Among days with similar temperatures and weekday status, variance in $Y_i$ is equal to the mean of $Y_i$.
Our data demonstrate potential overdispersion - the variance is larger than the mean.
Though not perfect, this model is an OK place to start.

Let's practice!

Bayesian Modeling with RJAGS