Multivariate Bayesian regression

Bayesian Modeling with RJAGS

Alicia Johnson

Associate Professor, Macalester College

Modeling volume

$Y_i$ = trail volume (# of users) on day $i$

¹ Photo courtesy commons.wikimedia.org

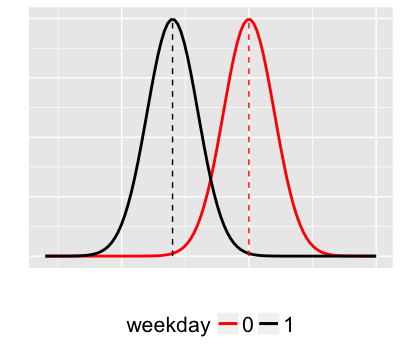
Modeling volume by weekday

$Y_i$ = trail volume (# of users) on day $i$
$X_i$ = 1 for weekdays, 0 for weekends

$\;$

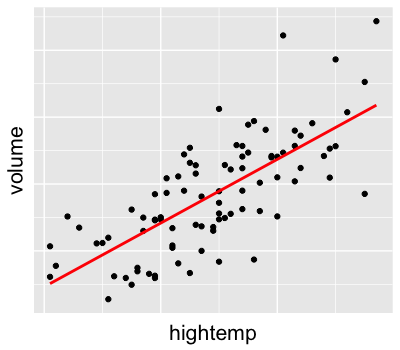
Modeling volume by temperature

$Y_i$ = trail volume (# of users) on day $i$
$Z_i$ = high temperature on day $i$ (in $^{\circ}$F)

$\;$

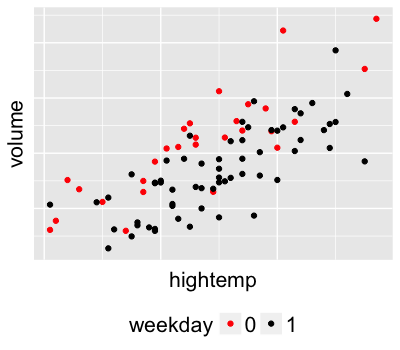
Modeling volume by temperature & weekday

$Y_i$ = trail volume (# of users) on day $i$
$X_i$ = 1 for weekdays, 0 for weekends
$Z_i$ = high temperature on day $i$ (in $^{\circ}$F)

$Y_i \sim N(m_i, s^2)$

$m_i = a + b X_i + c Z_i$

Weekends: $m_i = a + c Z_i$

Weekdays: $m_i = (a + b) + c Z_i$

Modeling volume by temperature & weekday

$Y_i$ = trail volume (# of users) on day $i$
$X_i$ = 1 for weekdays, 0 for weekends
$Z_i$ = high temperature on day $i$ (in $^{\circ}$F)

$Y_i \sim N(m_i, s^2)$

$m_i = a + b X_i + c Z_i$

Weekends: $m_i = a + c Z_i$

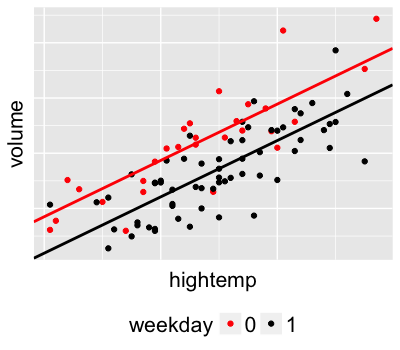
Weekdays: $m_i = (a + b) + c Z_i$

Modeling volume by temperature & weekday

$m_i = a + bX_i + cZ_i$

Weekends: $m_i = a + c Z_i$

Weekdays: $m_i = (a + b) + c Z_i$

$a$ = weekend y-intercept
$a+b$ = weekday y-int.
$b$ = contrast between weekday vs weekend y-intercepts

$c$ = common slope
$s$ = residual standard deviation

Priors for $a$ and $b$

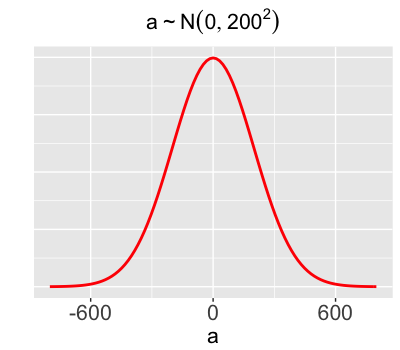
We lack certainty about the y-intercept for the relationship between temperature & weekend volume.

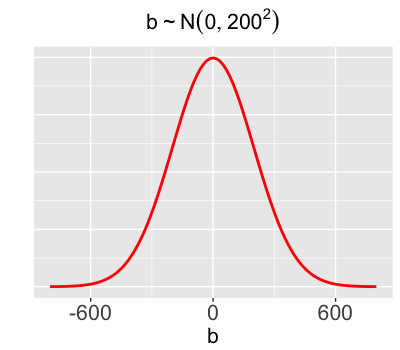
We lack certainty about how typical volume compares on weekdays vs weekends of similar temperature.

Priors for $c$ and $s$

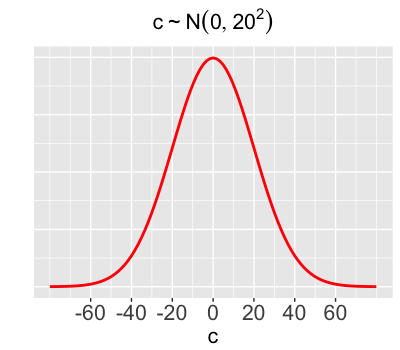
Whether on weekdays or weekends, we lack certainty about the association between trail volume & temperature.

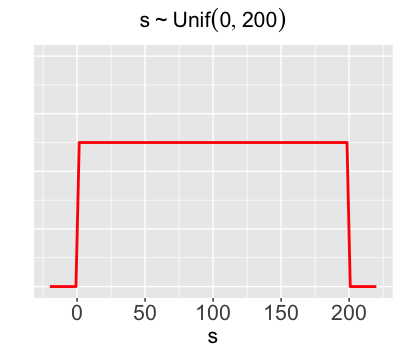
The typical deviation from the trend is equally likely to be anywhere between 0 and 200 users.

Bayesian model of volume by weekday status

$Y_i \sim N(m_i, s^2)$
$m_i = a + b X_i + c Z_i$
$a \sim N(0, 200^2)$
$b \sim N(0, 200^2)$
$c \sim N(0, 20^2)$
$s \sim \text{Unif}(0, 200)$

DEFINE the Bayesian model in RJAGS

$Y_i \sim N(m_i, s^2)$
$m_i = a + b X_i + c Z_i$
$a \sim N(0, 200^2)$
$b \sim N(0, 200^2)$
$c \sim N(0, 20^2)$
$s \sim \text{Unif}(0, 200)$

rail_model_2 <- "model{
  # Likelihood model for Y[i]
  for(i in 1:length(Y)) {
    Y[i] ~ dnorm(m[i], s^(-2))
    m[i] <- a + b[X[i]] + c * Z[i]
  }

  # Prior models for a, b, c, s
  a ~ dnorm(0, 200^(-2))
  b[1] <- 0
  b[2] ~ dnorm(0, 200^(-2))
  c ~ dnorm(0, 20^(-2))
  s ~ dunif(0, 200)
}"

Let's practice!

Bayesian Modeling with RJAGS