Markov chains

Bayesian Modeling with RJAGS

Alicia Johnson

Associate Professor, Macalester College

Posterior simulation

Normal-Normal model:

$Y_i$ = change in reaction time (ms)

$Y_i \sim N(m, s^2)$
$m \sim N(50, 25^2)$
$s \sim \text{Unif}(0, 200)$

Approximate posteriors:

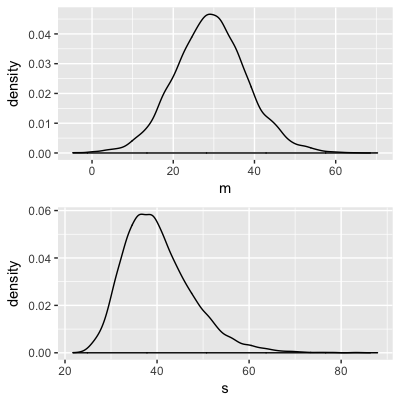
Markov chains

head(sleep_chains, 20)

m is a Markov chain, NOT a random sample from the posterior
RJAGS goal: Utilize Markov chains to approximate posteriors that are otherwise too complicated to define or sample

          m        s iter
1  17.25796 31.46256    1
2  34.58469 37.88655    2
3  36.45480 39.58056    3
4  25.00971 39.69494    4
5  29.95475 35.90001    5
6  28.43894 37.46466    6
7  38.32427 35.44081    7
8  27.90956 42.07951    8
9  28.09270 52.36360    9
10 29.70648 28.30665   10
11 32.10350 46.64174   11
12 34.41397 28.86993   12
13 23.33649 37.46498   13
14 39.26587 32.91031   14
15 27.95317 43.13887   15
16 18.91718 44.64376   16
17 28.63141 43.49800   17
18 41.22929 47.42336   18
19 33.12585 42.81980   19
20 35.86270 30.47737   20

Markov chain dependence

head(sleep_chains, 20)

          m        s iter
1  17.25796 31.46256    1
2  
3  
4
5
6
7
8
9
10
11
...

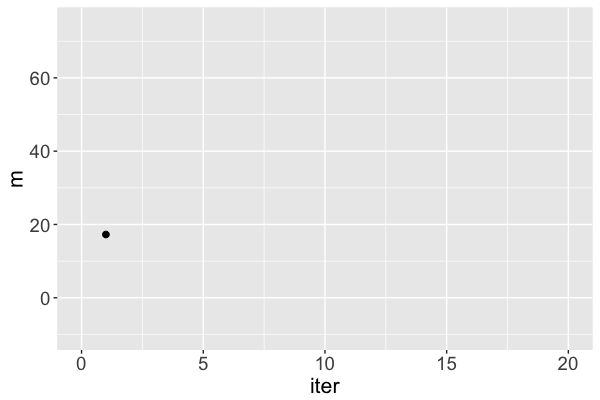
Markov chain dependence

head(sleep_chains, 20)

          m        s iter
1  17.25796 31.46256    1
2  34.58469 37.88655    2
3  
4
5
6
7
8
9
10
11
...

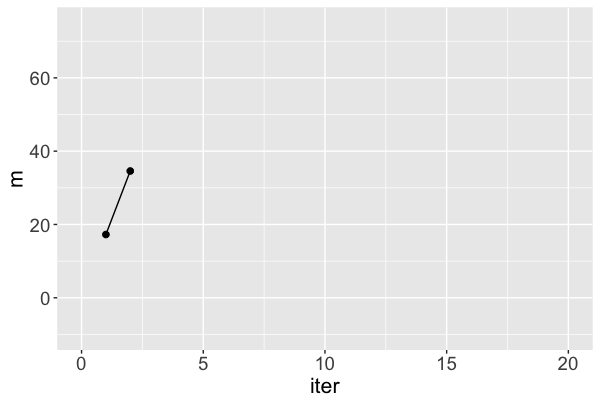
Markov chain dependence

head(sleep_chains, 20)

          m        s iter
1  17.25796 31.46256    1
2  34.58469 37.88655    2
3  36.45480 39.58056    3
4
5
6
7
8
9
10
11
...

          m        s iter
1  17.25796 31.46256    1
2  34.58469 37.88655    2
3  36.45480 39.58056    3
4  25.00971 39.69494    4
5  29.95475 35.90001    5
6  28.43894 37.46466    6
7  38.32427 35.44081    7
8  27.90956 42.07951    8
9  28.09270 52.36360    9
10 29.70648 28.30665   10
11 32.10350 46.64174   11
12 34.41397 28.86993   12
13 23.33649 37.46498   13
14 39.26587 32.91031   14
15 27.95317 43.13887   15
16 18.91718 44.64376   16
17 28.63141 43.49800   17
18 41.22929 47.42336   18
19 33.12585 42.81980   19
20 35.86270 30.47737   20

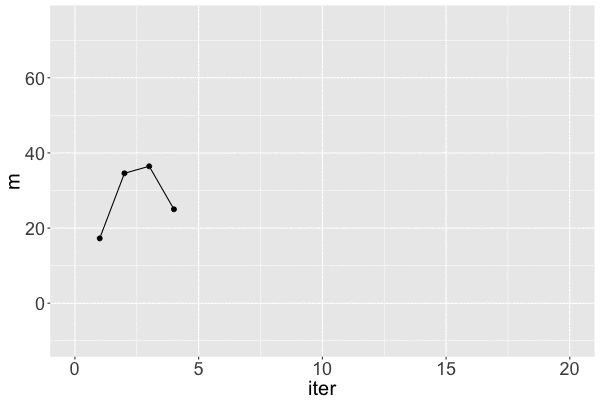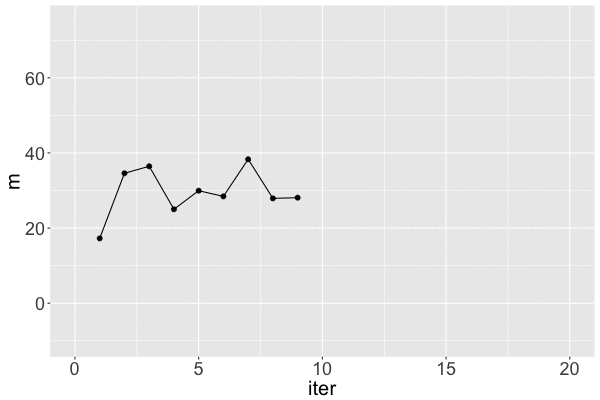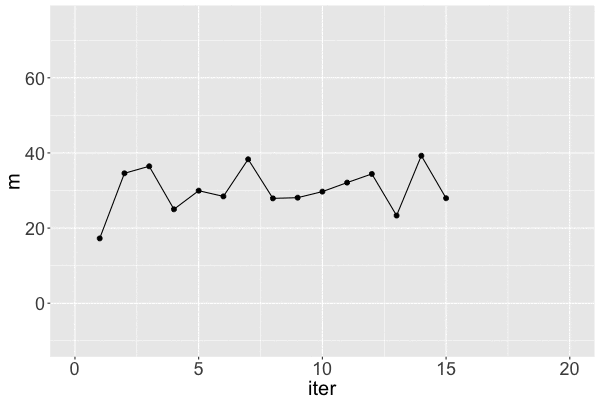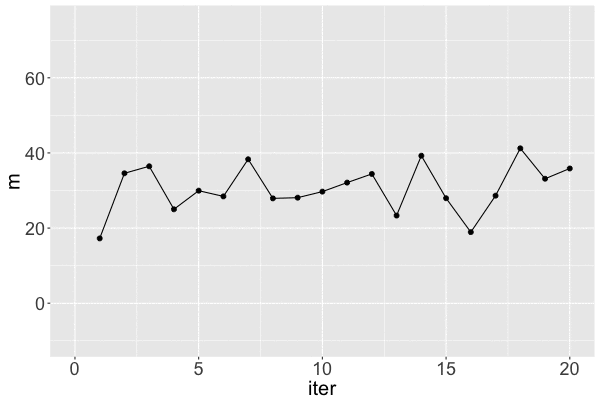
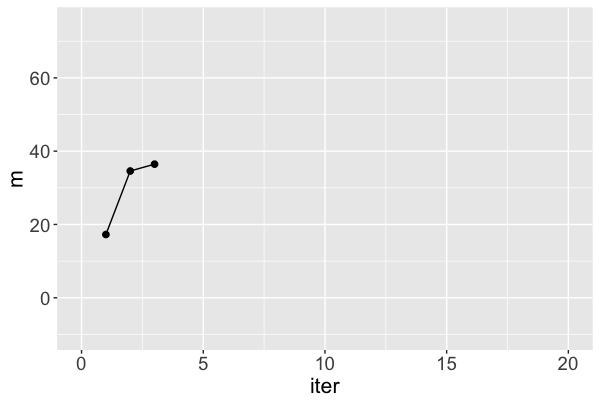
Markov chain dependence

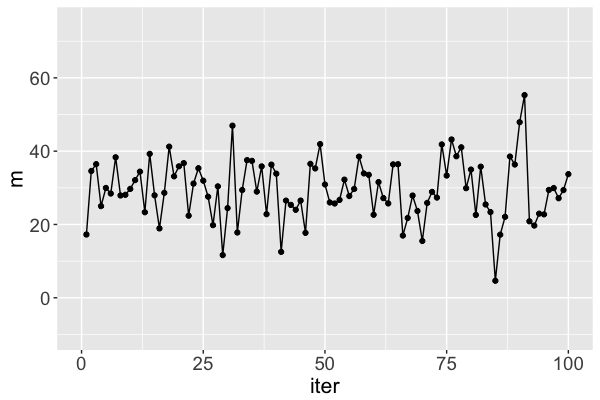
Markov chain trace plot

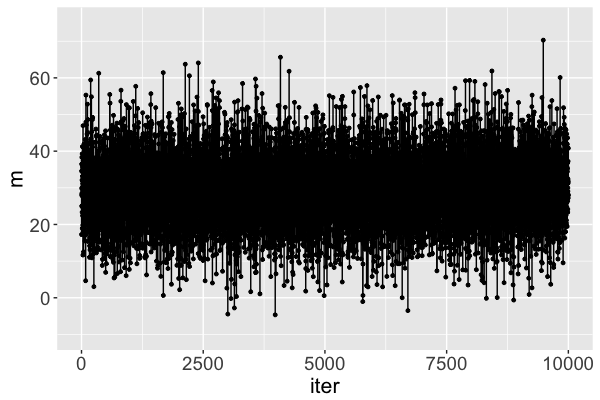
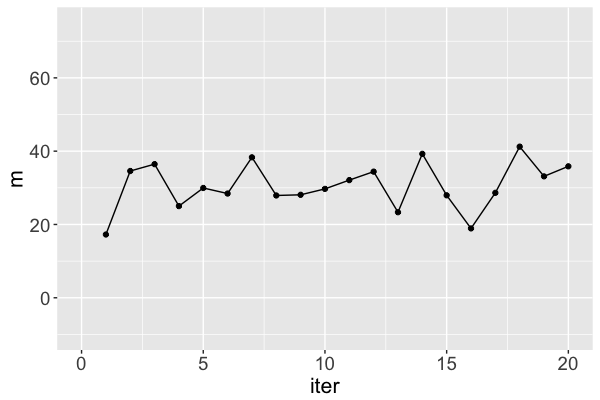
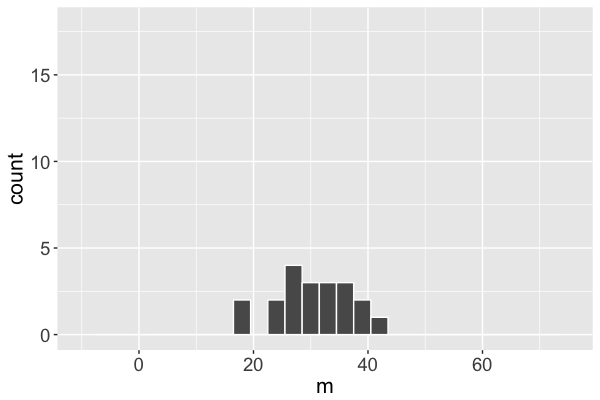
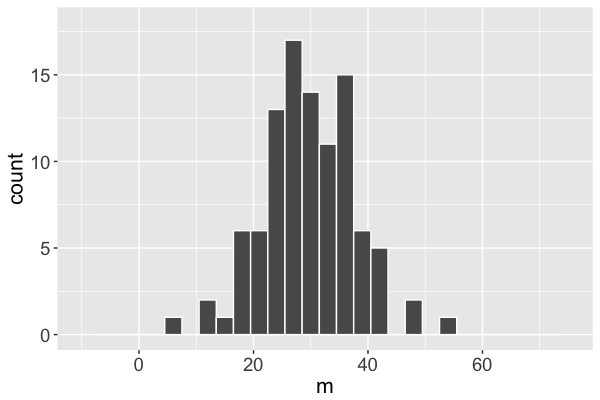
Markov chain distribution

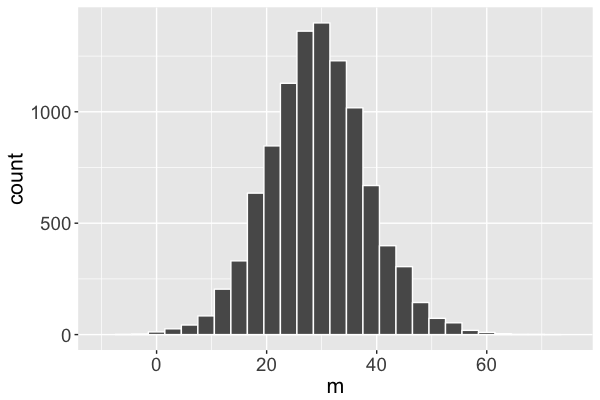
Markov chain distribution: an approximation of the posterior!

The $m$ Markov chain...

traverses the sample space of $m$,

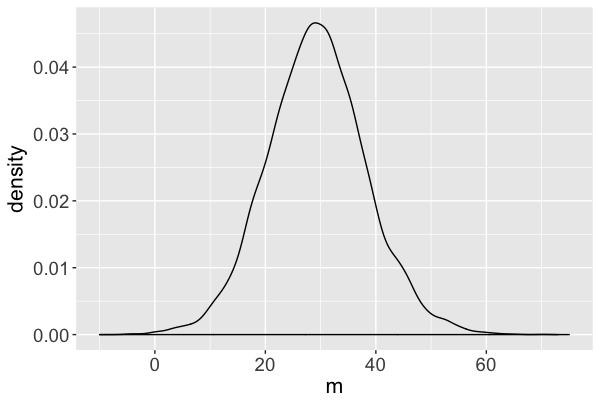
mimics a random sample, and

converges to the posterior.

Let's practice!

Bayesian Modeling with RJAGS