Data & the likelihood

Bayesian Modeling with RJAGS

Alicia Johnson

Associate Professor, Macalester College

Polling data

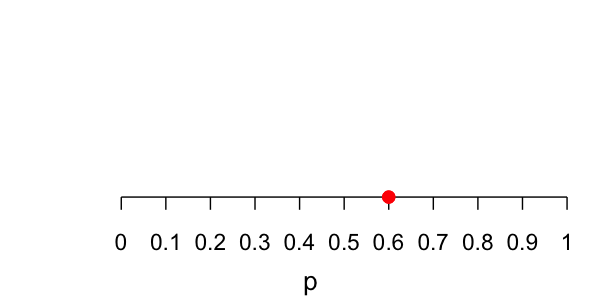
Parameter
$p$ = proportion that support you
Data
$X = 6$ of $n = 10$ polled voters plan to vote for you
Insights
You are more likely to have observed these data if $p \approx 0.6$ than if $p < 0.5$.

Modeling the dependence of X on p

Poll assumptions:
voters are independent
$p$ = probability that a voter supports you
$X$ = number of $n$ polled voters that support you
(count of successes in $n$ independent trials, each having probability of success $p$)
Conditional distribution of $X$ given $p$:
$X \sim \text{Bin}(n,p)$

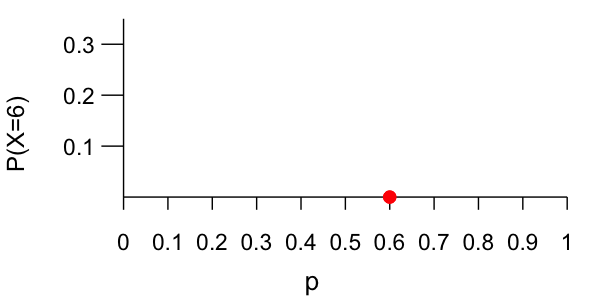
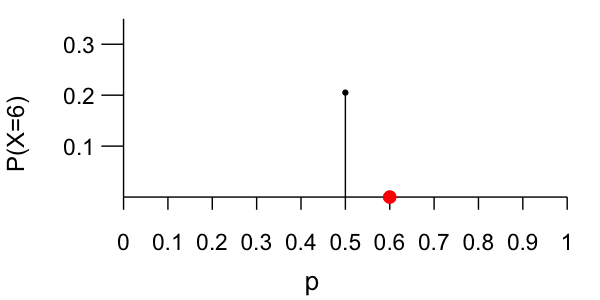
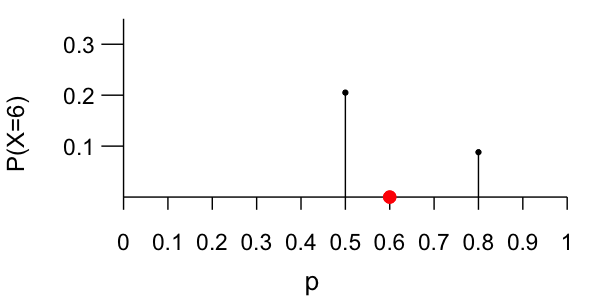
Dependence of X on p

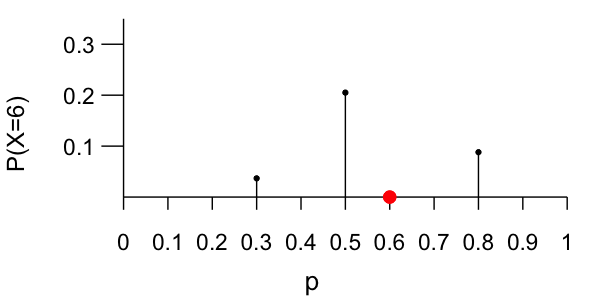
What's the likelihood?

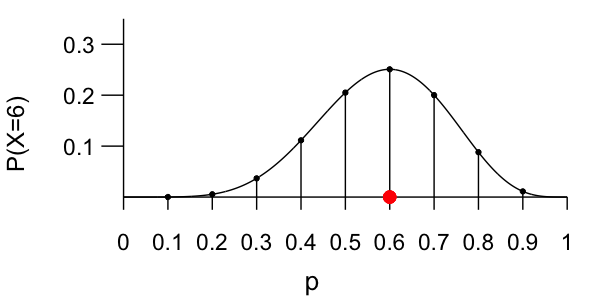
Likelihood

The likelihood function summarizes the likelihood of observing polling data $X$ under different values of the underlying support parameter $p$. It is a function of $p$.

High likelihood $\Rightarrow$ $p$ is compatible with the data
Low likelihood $\Rightarrow$ $p$ is not compatible with the data

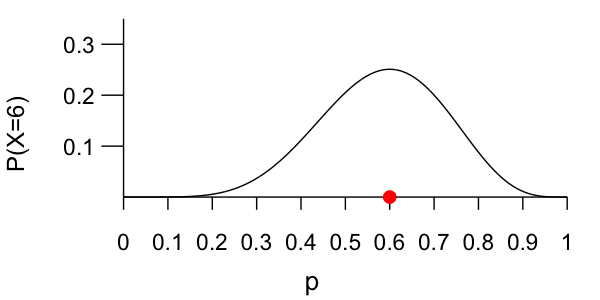
Let's practice!

Bayesian Modeling with RJAGS