Simulating the Normal-Normal in RJAGS

Bayesian Modeling with RJAGS

Alicia Johnson

Associate Professor, Macalester College

Sleep study

$Y_i$ = change in reaction time (ms) after 3 days of sleep deprivation

$Y_i \sim N(m, s^2)$

Insights from the priors

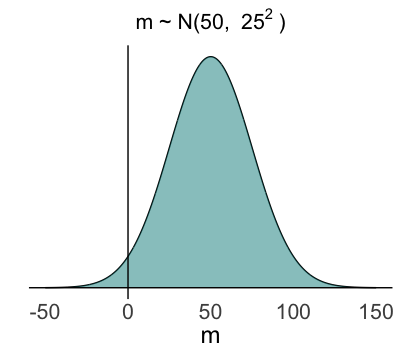
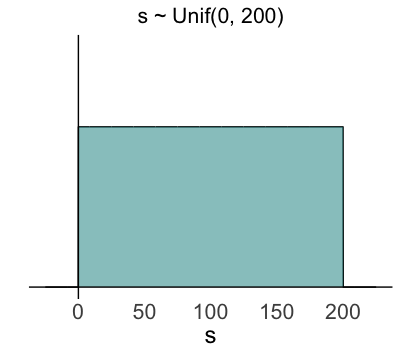
Insights from the data (& likelihood)

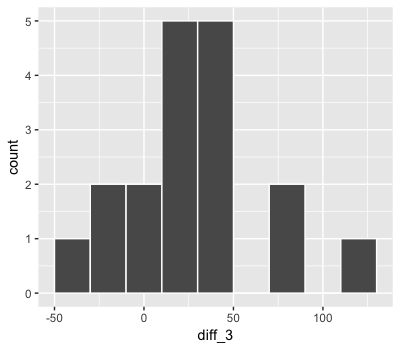
mean(sleep_study$diff_3)
sd(sleep_study$diff_3)

26.34021
37.20764

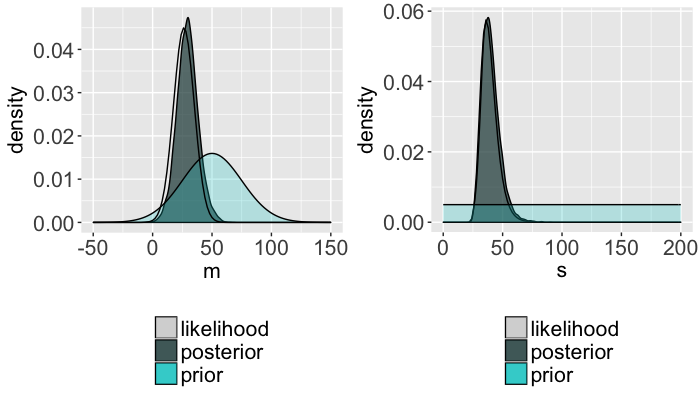
Assuming these data are generated from $Y_i \sim N(m, s^2)$, they are most likely to have occurred if...

$m \approx 26$ ms
$s \approx 37$ ms

Posterior insights

DEFINE the Normal-Normal

sleep_model <- "model{
    # Likelihood model for Y[i]




    # Prior models for m and s


}"

DEFINE the Normal-Normal

sleep_model <- "model{
    # Likelihood model for Y[i]




    # Prior models for m and s


}"

$Y_i \sim N(m, s^2)$ for $i$ in ${1,2,\ldots,18}$

DEFINE the Normal-Normal

sleep_model <- "model{
    # Likelihood model for Y[i]
    for(i in 1:length(Y)) {

    }

    # Prior models for m and s


}"

$Y_i \sim N(m, s^2)$ for $i$ in ${1,2,\ldots,18}$

DEFINE the Normal-Normal

sleep_model <- "model{
    # Likelihood model for Y[i]
    for(i in 1:length(Y)) {
        Y[i] ~ dnorm(m, s^(-2))
    }

    # Prior models for m and s


}"

$Y_i \sim N(m, s^2)$ for $i$ in ${1,2,\ldots,18}$
- NOTE: precision = variance$^{-1}$ = $s^{-2}$

DEFINE the Normal-Normal

sleep_model <- "model{
    # Likelihood model for Y[i]
    for(i in 1:length(Y)) {
        Y[i] ~ dnorm(m, s^(-2))
    }

    # Prior models for m and s
    m ~ dnorm(50, 25^(-2))

}"

$Y_i \sim N(m, s^2)$ for $i$ in ${1,2,\ldots,18}$
- NOTE: precision = variance$^{-1}$ = $s^{-2}$
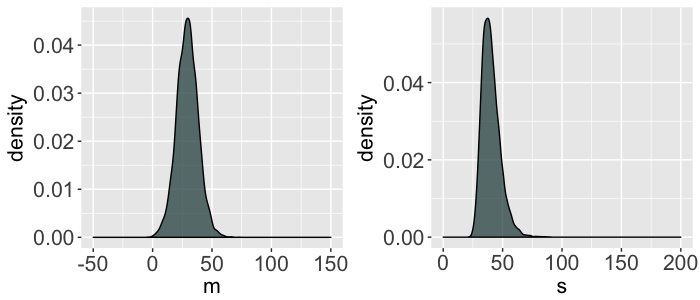
$m \sim N(50, 25^2)$

DEFINE the Normal-Normal

sleep_model <- "model{
    # Likelihood model for Y[i]
    for(i in 1:length(Y)) {
        Y[i] ~ dnorm(m, s^(-2))
    }

    # Prior models for m and s
    m ~ dnorm(50, 25^(-2))
    s ~ dunif(0, 200)
}"

$Y_i \sim N(m, s^2)$ for $i$ in ${1,2,\ldots,18}$
- NOTE: precision = variance$^{-1}$ = $s^{-2}$
$m \sim N(50, 25^2)$
$s \sim \text{Unif}(0, 200)$

COMPILE the Normal-Normal

# COMPILE the model    
sleep_jags <- jags.model(textConnection(sleep_model), 
    data = list(Y = sleep_study$diff_3), 
    inits = list(.RNG.name = "base::Wichmann-Hill",
                 .RNG.seed = 1989))
    sleep_study$diff_3

 [1]  71.8798 -18.0269  33.7877 -36.4096  32.5074  74.9082
 [7]  15.9673 -10.8008  29.1938  33.7556  18.8188  -0.7697
[13]  30.0626 125.1784   5.7331  15.2090  11.9091  41.2199

SIMULATE the Normal-Normal

# COMPILE the model    
sleep_jags <- jags.model(textConnection(sleep_model), 
    data = list(Y = sleep_study$diff_3),
    inits = list(.RNG.name = "base::Wichmann-Hill", 
                 .RNG.seed = 1989))

# SIMULATE the posterior
sleep_sim <- coda.samples(model = sleep_jags, 
    variable.names = c("m", "s"), 
    n.iter = 10000)

SIMULATE the Normal-Normal

Let's practice!

Bayesian Modeling with RJAGS