The Normal-Normal model
Bayesian Modeling with RJAGS

Alicia Johnson
Associate Professor, Macalester College
Chapter 2 goals
- Engineer the two-parameter Normal-Normal model
- Define, compile, and simulate the Normal-Normal in RJAGS
- Explore Markov chains, the mechanics of an RJAGS simulation
Sleep deprivation
Research Question
How does sleep deprivation impact reaction time?
The Study
- Measure reaction time on Day 0
- Restrict sleep to 3 hours per night
- Measure reaction time on Day 3
- Measure the change in reaction time
Modeling change in reaction time
$Y_i$ = change in reaction time (ms)
Assume
$Y_i$ are Normally distributed around some average change in reaction time $m$ with standard deviation $s$.
$$Y_i \sim N(m, s^2)$$
Prior model for parameter $m$
$Y_i$ = change in reaction time (ms)
$Y_i \sim N(m, s^2)$
$m$ = average $Y_i$
Prior information:
- With normal sleep, average reaction time is ~250 ms
- Expect average to $\nearrow$ by ~50 ms
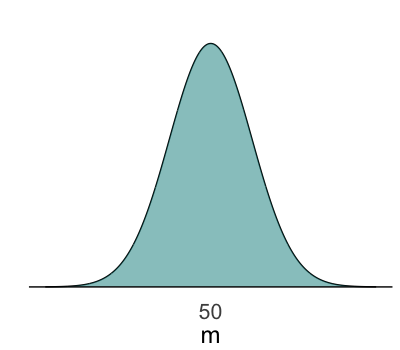
Prior model for parameter $m$
$Y_i$ = change in reaction time (ms)
$Y_i \sim N(m, s^2)$
$m$ = average $Y_i$
Prior information:
- With normal sleep, average reaction time is ~250 ms
- Expect average to $\nearrow$ by ~50 ms
- Average is unlikely to $\searrow$ & unlikely to $\nearrow$ by > ~150 ms
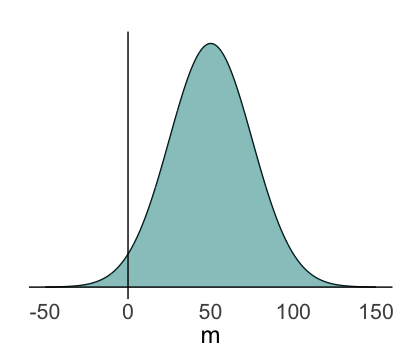
Prior model for parameter $m$
$Y_i$ = change in reaction time (ms)
$Y_i \sim N(m, s^2)$
$m$ = average $Y_i$
Prior information:
- With normal sleep, average reaction time is ~250 ms
- Expect average to $\nearrow$ by ~50 ms
- Average is unlikely to $\searrow$ & unlikely to $\nearrow$ by > ~150 ms
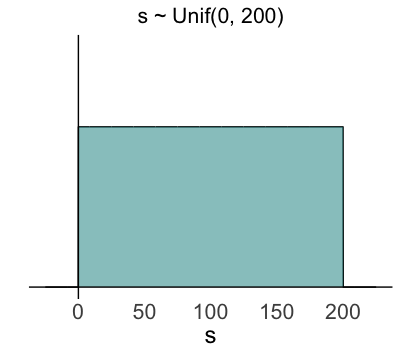
Prior model for parameter $s$
$Y_i$ = change in reaction time (ms)
$Y_i \sim N(m, s^2)$
$s$ = standard deviation of $Y_i$
Prior information:
- $s > 0$
- With normal sleep, s.d. in reaction times is ~30 ms
- $s$ is equally likely to be anywhere from 0 to 200 ms
The Normal-Normal Model
Likelihood:
$Y_i \sim N(m, s^2)$
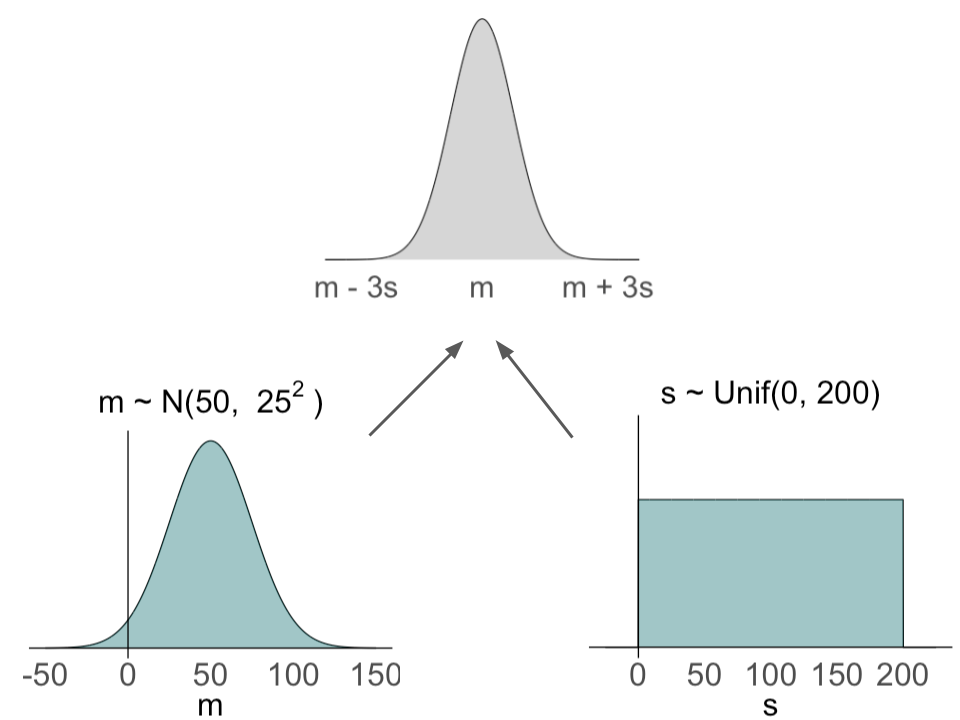
The Normal-Normal Model
Likelihood:
$Y_i \sim N(m, s^2)$
Priors:
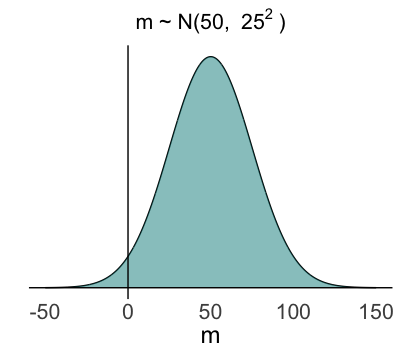
$m \sim N(50, 25^2)$
$s \sim \text{Unif}(0, 200)$
Let's practice!
Bayesian Modeling with RJAGS

