Bayesian regression with a categorical predictor

Bayesian Modeling with RJAGS

Alicia Johnson

Associate Professor, Macalester College

Chapter 4 goals

Incorporate categorical predictors into Bayesian models
Engineer multivariate Bayesian regression models
Extend our methodology for Normal regression models to generalized linear models: Poisson regression

Rail-trail volume

Goal:
Explore daily volume on a rail-trail in Massachusetts.

¹ Photo courtesy commons.wikimedia.org

Modeling volume

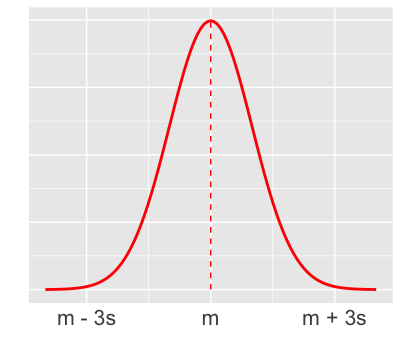
$Y_i$ = trail volume (# of users) on day $i$ $ \; $
$ \;$

Model
$Y_i \sim N(m_i, s^2)$

Modeling volume by weekday

$Y_i$ = trail volume (# of users) on day $i$
$X_i$ = 1 for weekdays, 0 for weekends

Model
$Y_i \sim N(m_i, s^2)$

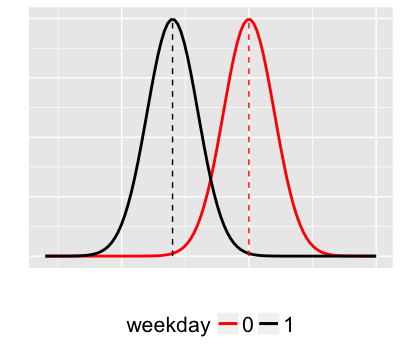
Modeling volume by weekday

$Y_i$ = trail volume (# of users) on day $i$
$X_i$ = 1 for weekdays, 0 for weekends

Model
$Y_i \sim N(m_i, s^2)$

Modeling volume by weekday

$Y_i$ = trail volume (# of users) on day $i$
$X_i$ = 1 for weekdays, 0 for weekends

Model
$Y_i \sim N(m_i, s^2)$
$m_i = a + bX_i$

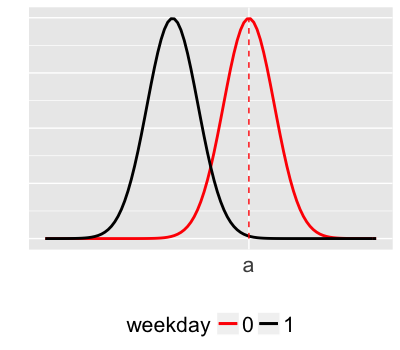
Modeling volume by weekday

$Y_i$ = trail volume (# of users) on day $i$
$X_i$ = 1 for weekdays, 0 for weekends

Model
$Y_i \sim N(m_i, s^2)$
$m_i = a + bX_i$

$a$ = typical weekend volume

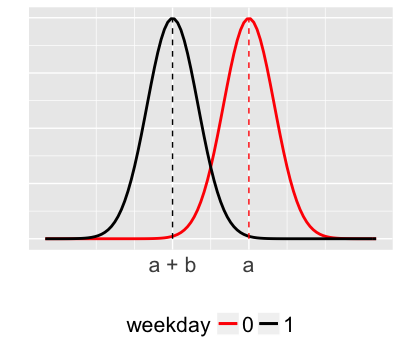
$Y_i$ = trail volume (# of users) on day $i$
$X_i$ = 1 for weekdays, 0 for weekends

Model
$Y_i \sim N(m_i, s^2)$
$m_i = a + bX_i$

$a$ = typical weekend volume
$a + b$ = typical weekday volume

$b$ = contrast between typical weekday vs weekend volume
$s$ = residual standard deviation

Priors for $a$ & $b$

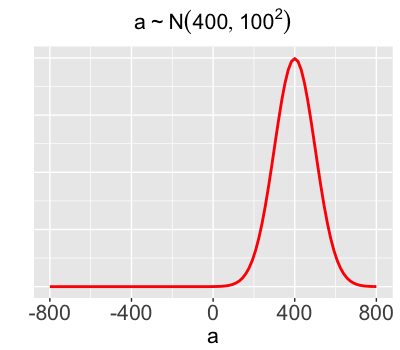
Typical weekend volume is most likely around 400 users per day, but possibly as low as 100 or as high as 700 users.

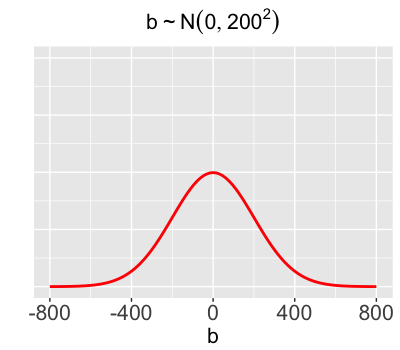
We lack certainty about how weekday volume compares to weekend volume. It could be more, it could be less.

Prior for $s$

$\;$

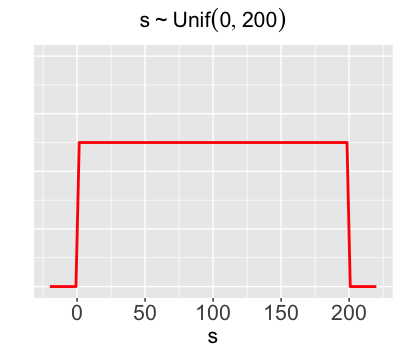
The standard deviation in volume from day to day (whether on weekdays or weekends) is equally likely to be anywhere between 0 and 200 users.

Bayesian model of volume by weekday status

$Y_i \sim N(m_i, s^2)$
$m_i = a + b X_i$
$a \sim N(400, 100^2)$
$b \sim N(0, 200^2)$
$s \sim \text{Unif}(0, 200)$

DEFINE the Bayesian model in RJAGS

$Y_i \sim N(m_i, s^2)$
$m_i = a + b X_i$
$a \sim N(400, 100^2)$
$b \sim N(0, 200^2)$
$s \sim \text{Unif}(0, 200)$

rail_model_1 <- "model{
    # Likelihood model for Y[i]





    # Prior models for a, b, s




}"

DEFINE the Bayesian model in RJAGS

$Y_i \sim N(m_i, s^2)$
$m_i = a + b X_i$
$a \sim N(400, 100^2)$
$b \sim N(0, 200^2)$
$s \sim \text{Unif}(0, 200)$

rail_model_1 <- "model{
    # Likelihood model for Y[i]
    for(i in 1:length(Y)) {
        Y[i] ~ dnorm(m[i], s^(-2))

    }

    # Prior models for a, b, s
    a ~ dnorm(400, 100^(-2))
    s ~ dunif(0, 200)


}"

DEFINE the Bayesian model in RJAGS

m[i] <- a + b[X[i]]

X[1] = weekend, X[2] = weekday
b has 2 levels: b[1], b[2]
weekend trend ($m_i = a$)
m[i] <- a + b[1]

rail_model_1 <- "model{
    # Likelihood model for Y[i]
    for(i in 1:length(Y)) {
        Y[i] ~ dnorm(m[i], s^(-2))
        m[i] <- a + b[X[i]]
    }

    # Prior models for a, b, s
    a ~ dnorm(400, 100^(-2))
    s ~ dunif(0, 200)


}"

DEFINE the Bayesian model in RJAGS

m[i] <- a + b[X[i]]

X[1] = weekend, X[2] = weekday
b has 2 levels: b[1], b[2]
weekend trend ($m_i = a$)
m[i] <- a + b[1]
b[1] <- 0

rail_model_1 <- "model{
    # Likelihood model for Y[i]
    for(i in 1:length(Y)) {
        Y[i] ~ dnorm(m[i], s^(-2))
        m[i] <- a + b[X[i]]
    }

    # Prior models for a, b, s
    a ~ dnorm(400, 100^(-2))
    s ~ dunif(0, 200)
    b[1] <- 0

}"

DEFINE the Bayesian model in RJAGS

m[i] <- a + b[X[i]]

X[1] = weekend,X[2] = weekday
b has 2 levels: b[1], b[2]
weekend trend ($m_i = a$)
m[i] <- a + b[1]
b[1] <- 0
weekday ($m_i = a + b$)
m[i] <- a + b[2]

rail_model_1 <- "model{
    # Likelihood model for Y[i]
    for(i in 1:length(Y)) {
        Y[i] ~ dnorm(m[i], s^(-2))
        m[i] <- a + b[X[i]]
    }

    # Prior models for a, b, s
    a ~ dnorm(400, 100^(-2))
    s ~ dunif(0, 200)
    b[1] <- 0
    b[2] ~ dnorm(0, 200^(-2))
}"

b[2] ~ dnorm(0, 200^(-2))

Let's practice!

Bayesian Modeling with RJAGS

Preparing Video For Download...