Multivariate t-distributions

Multivariate Probability Distributions in R

Surajit Ray

Reader, University of Glasgow

Parameters for multivariate distributions

Distribution	Location Parameter	Scale Parameter
Normal	`mean`	`sigma`
t	`delta`	`sigma`
Skew-normal	`xi`	`Omega`
Skew-t	`xi`	`Omega`

Parameters for multivariate distributions

Distribution	Location Parameter	Scale Parameter	Degrees of freedom
Normal	`mean`	`sigma`	No
t	`delta`	`sigma`	Yes
Skew-normal	`xi`	`Omega`	No
Skew-t	`xi`	`Omega`	Yes

Comparing univariate normal with univariate t-distributions

Comparision

Standard normal
t with different df's

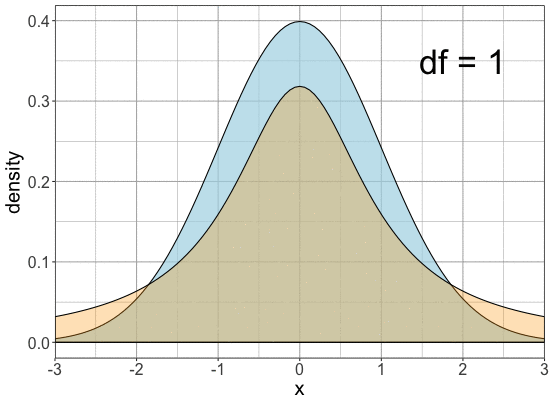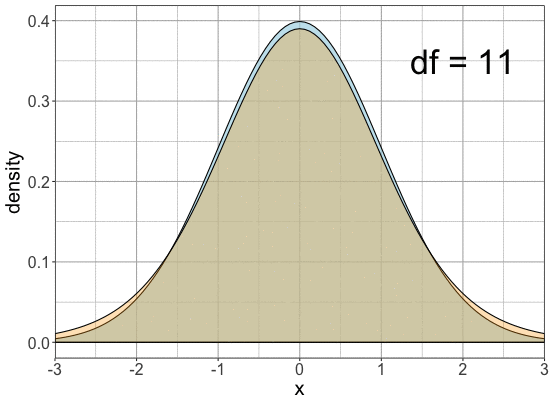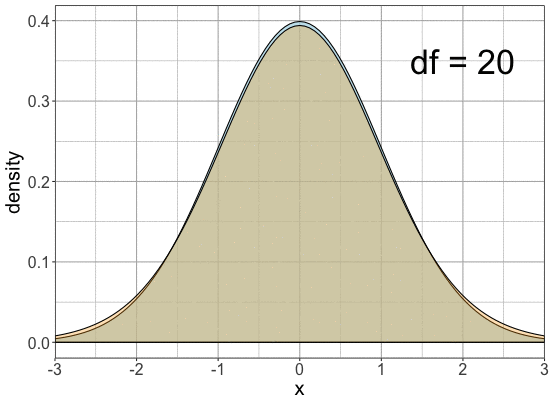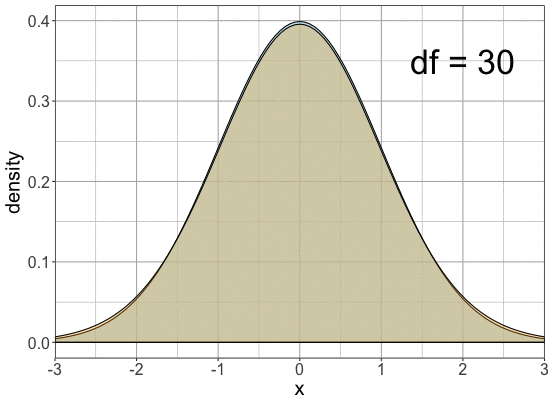
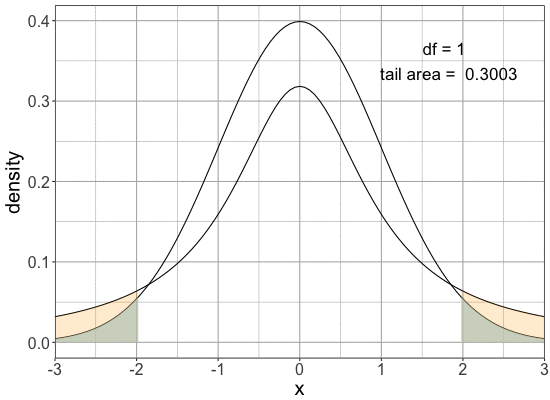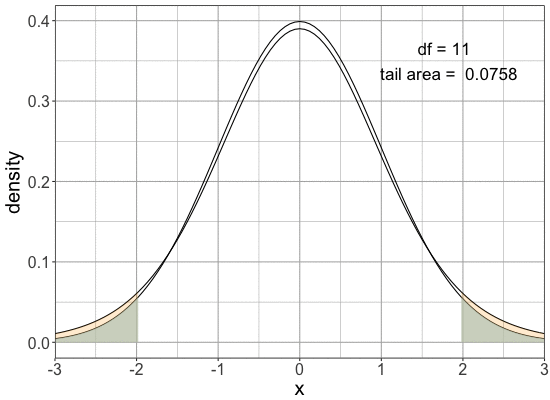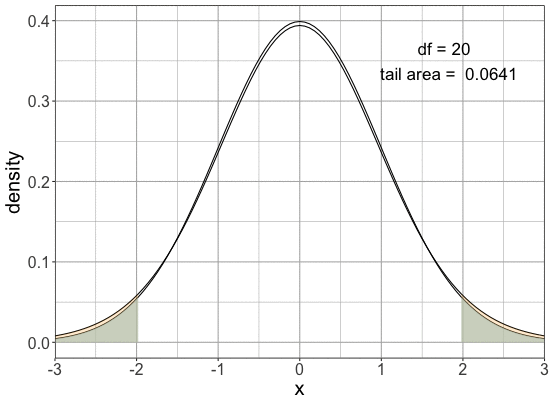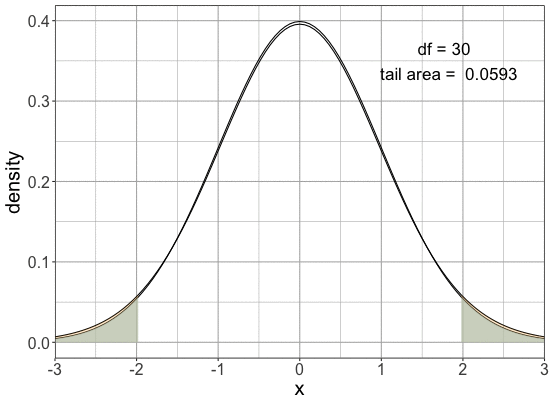
Comparing normal and t-distribution tails

Tails are fatter for the same cutoff

$P(X< - 1.96 \text{ or } X > 1.96)$

Distribution	Probability
Normal	0.05
t(df=1)	0.3
t(df=8)	0.0857
t(df=20)	0.0641
t(df=30)	0.0593

Multivariate t-distribution notation

Generalization of the univariate Student's t-distribution
- Widely used version has only one degree of freedom for all dimensions and is denoted by

$$t_{df}(\delta, \Sigma ) $$

Contours of bivariate normal and t-distributions

${\mu}=\delta={\begin{pmatrix} 1 \\ 2 \end{pmatrix}},\quad { \Sigma }={\begin{pmatrix} 1 & 0.5 \\ 0.5 & 2 \end{pmatrix}}$

Contours of a t with df = 3

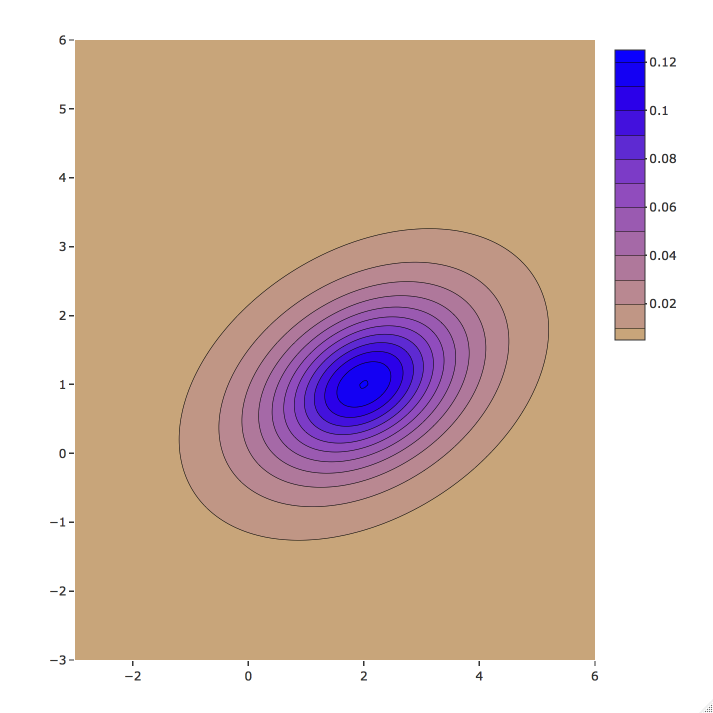
${\begin{matrix} ~ \\ ~ \end{matrix}}$

Contours of a bivariate normal

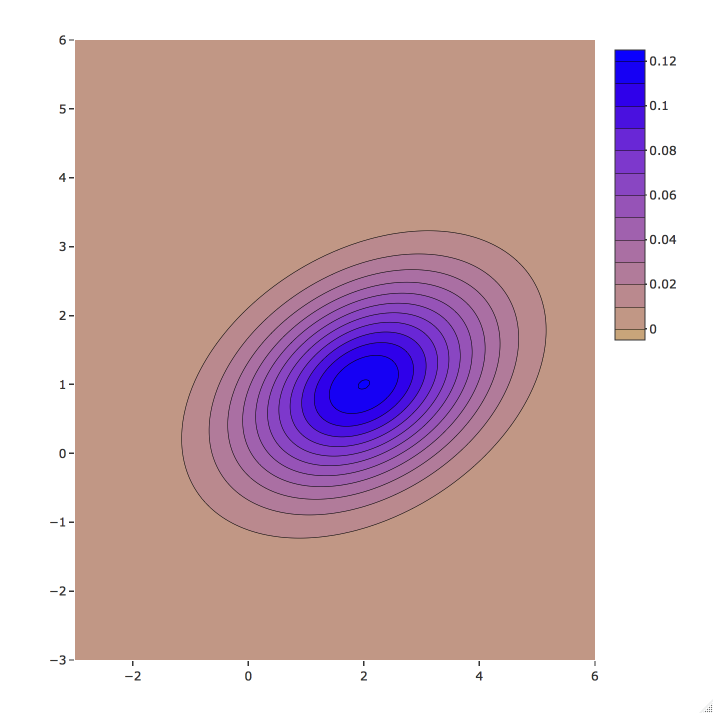
Functions for multivariate t-distributions

Functions include:
- rmvt(n, delta, sigma, df)
- dmvt(x, delta, sigma, df)
- qmvt(p, delta, sigma, df)
- pmvt(upper, lower, delta, sigma, df)

Generating random samples

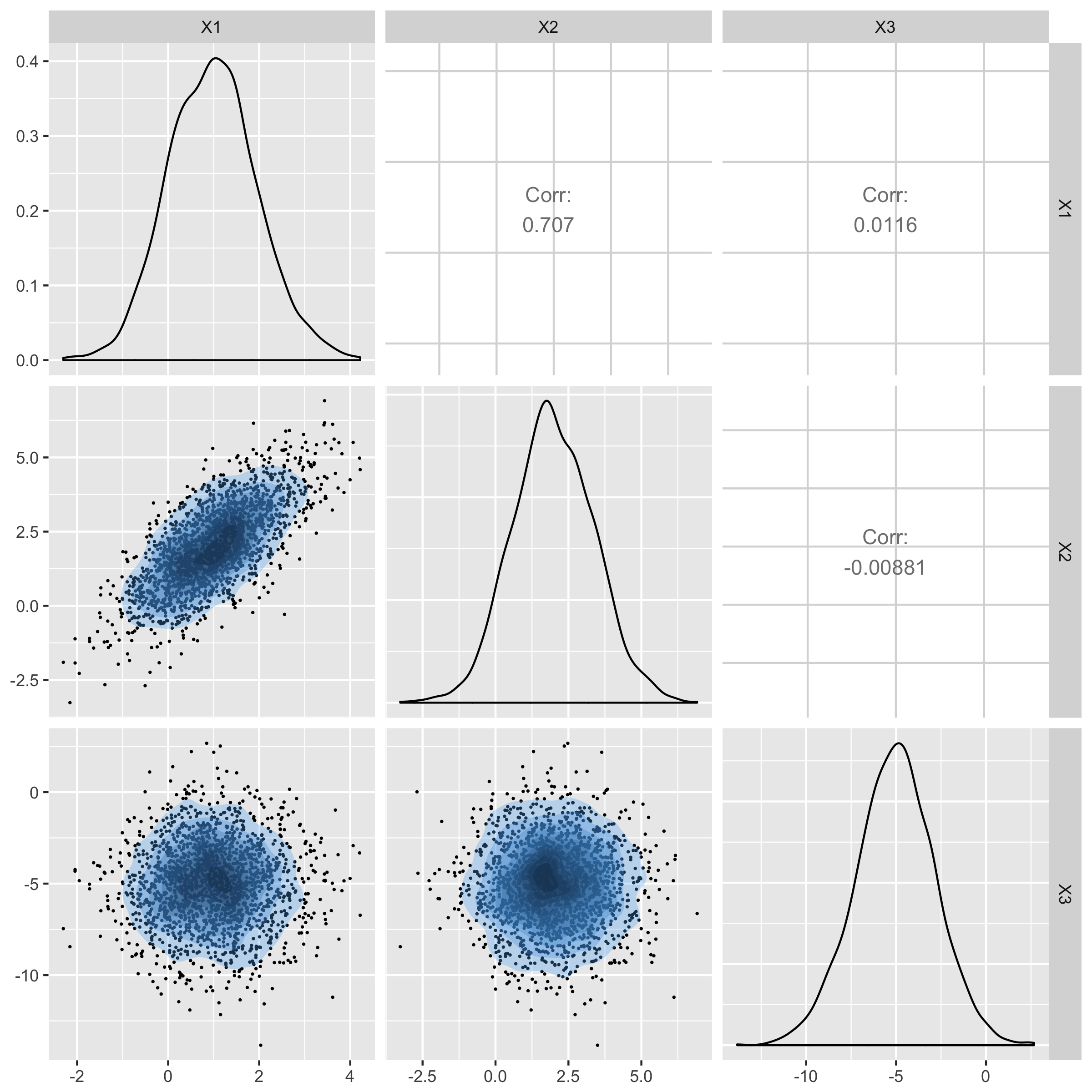
Generate samples from 3 dimensional t with $ \delta= \begin{pmatrix} 1 \\ 2 \\ -5 \end{pmatrix} ,~~\Sigma={\begin{pmatrix} 1 & 1 & 0 \\ 1 & 2 & 0 \\ 0 & 0 & 5 \end{pmatrix}}, ~~df = 4.$

# Specify delta and sigma
delta <- c(1, 2, -5) 
sigma <- matrix(c(1, 1, 0,
                  1, 2, 0,
                  0, 0, 5), 3, 3)

# Generate samples                  
t.sample <- rmvt(n = 2000, delta = delta, sigma = sigma, df = 4)
head(t.sample,4)

       [,1]   [,2]    [,3]
[1,] -1.256 -1.518 -12.340
[2,]  1.479  1.908  -7.647
[3,] -0.152  1.357  -9.011
[4,]  1.938  2.531  -4.534

Comparing with normal samples

t-distribution with 4 degrees of freedom

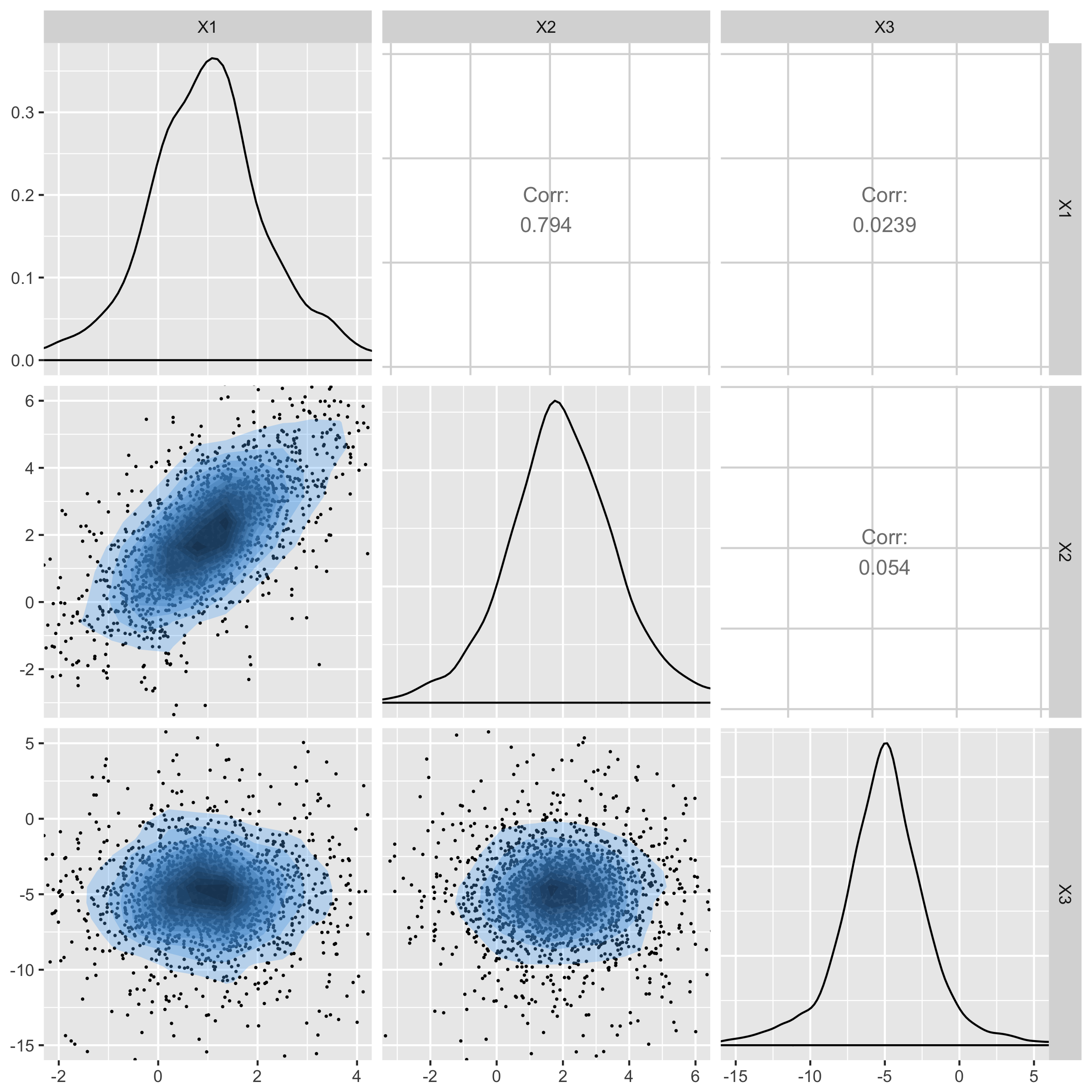
Normal distribution

Comparing with normal samples

t-distribution with 10 degrees of freedom

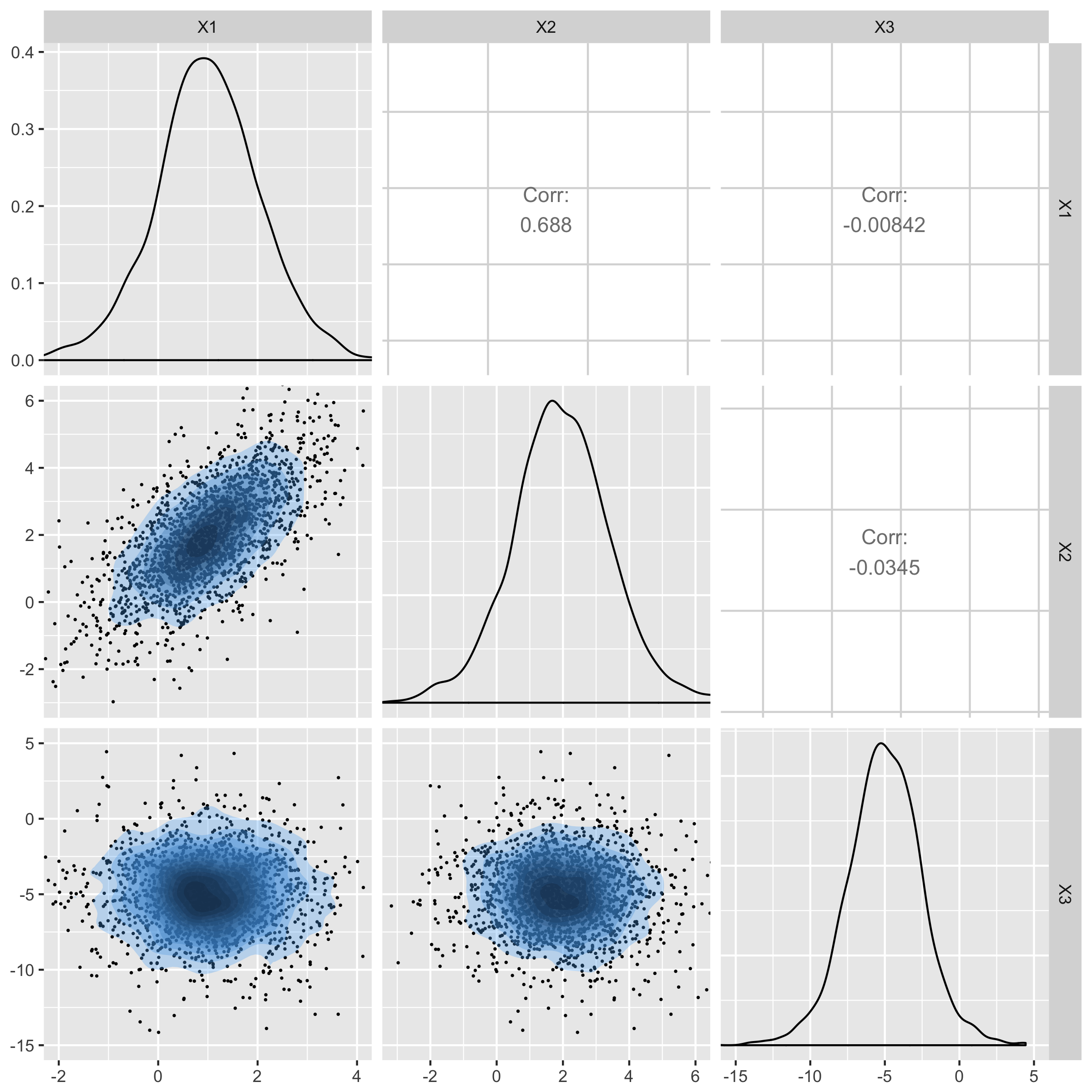
Normal distribution

Let's generate samples from a multivariate t-distribution!

Multivariate Probability Distributions in R