Cumulative Distribution and Inverse CDF

Multivariate Probability Distributions in R

Surajit Ray

Reader, University of Glasgow

When do we need to calculate CDF and inverse CDF?

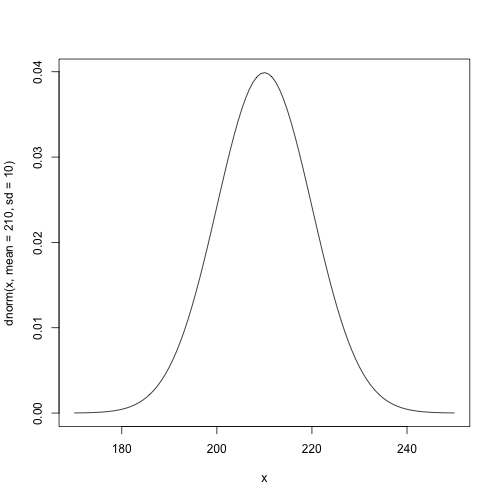Normal density with $\mu=210$ and $\sigma=10$

When do we need to calculate CDF and inverse CDF?

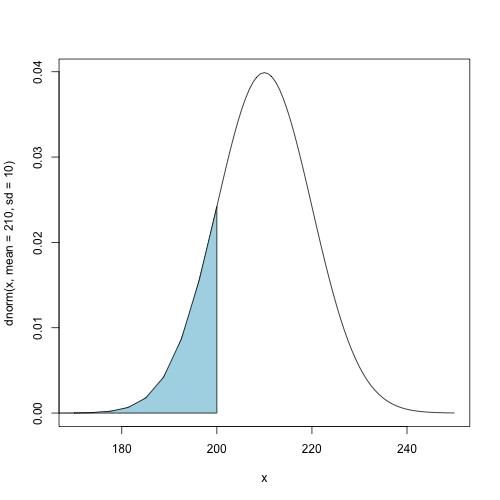Area under the curve for $x < 200$

When do we need to calculate CDF and inverse CDF?

pnorm(200, mean = 210, sd = 10)

[1] 0.159

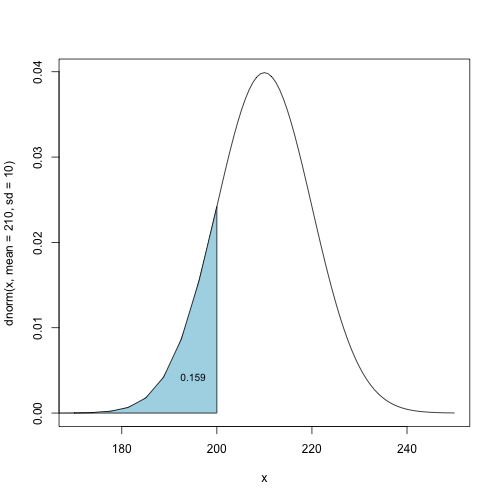
When do we need to calculate CDF and inverse CDF?

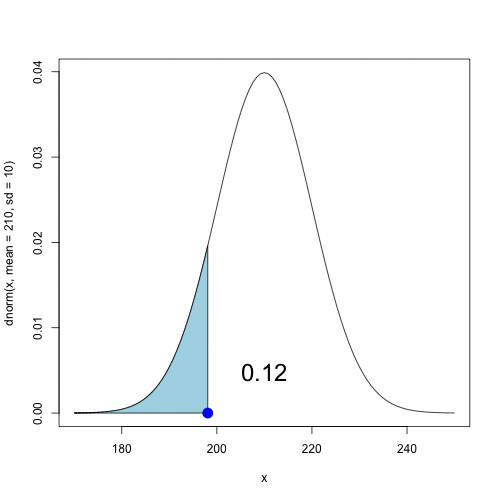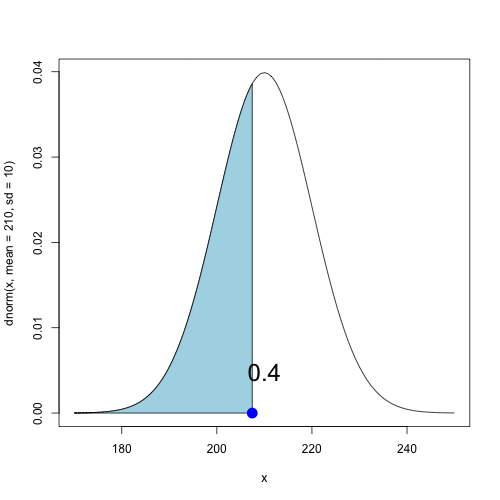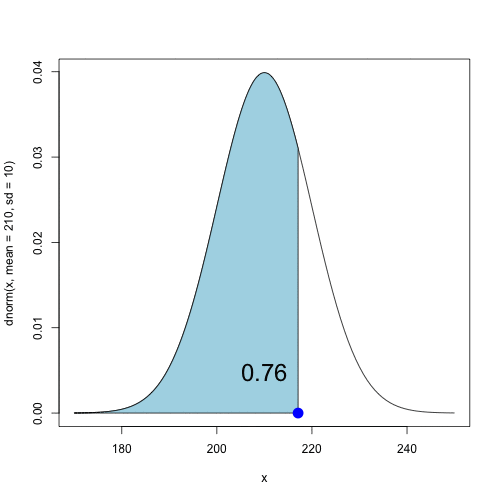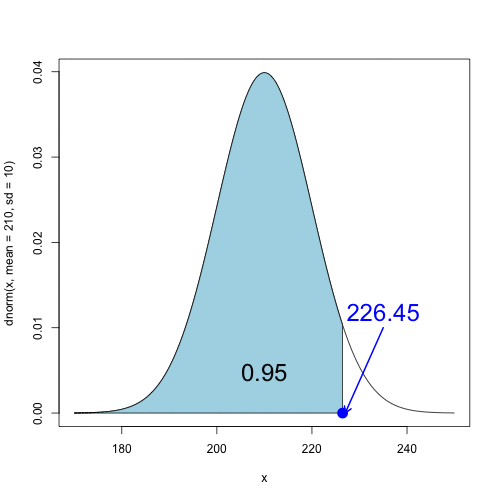
What is the $x_0$ such that the cumulative probability at $x_0$ is 0.95?

qnorm( p = 0.95, mean = 210, sd = 10)

[1] 226.45

$\Rightarrow$ 95% of the coffee jars will have less than 226.45 grams of coffee

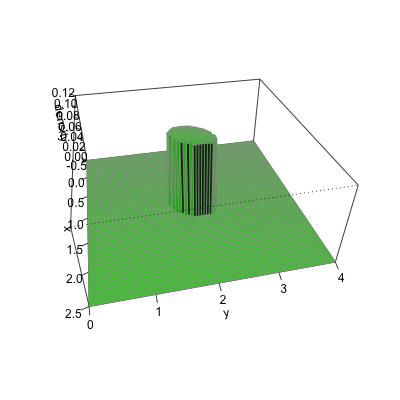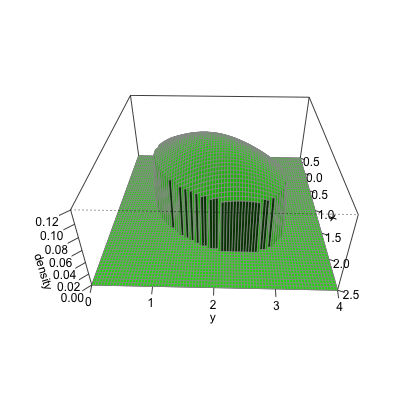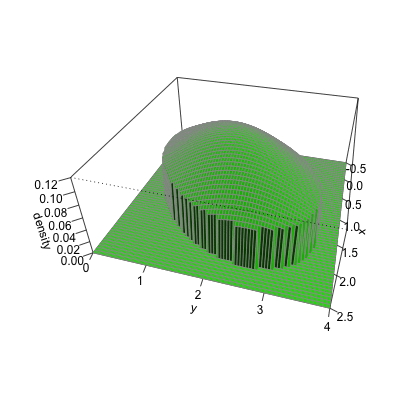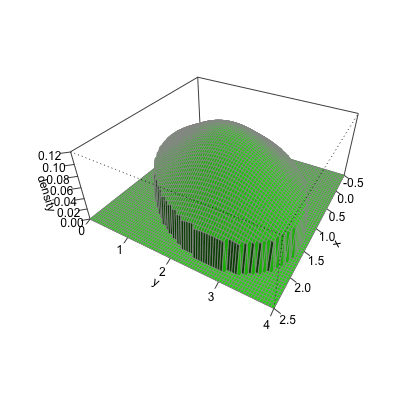
Cumulative distribution for a bivariate normal

Bivariate CDF at x = 2 and y = 4 for a normal with ${\mu}={\begin{pmatrix} 1 \\ 2 \end{pmatrix}},\quad { \Sigma }={\begin{pmatrix} 1 & .5 \\ .5 & 2 \end{pmatrix}}$

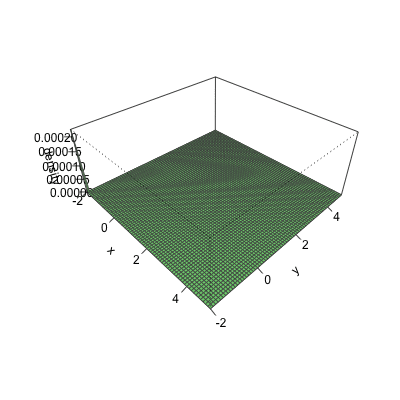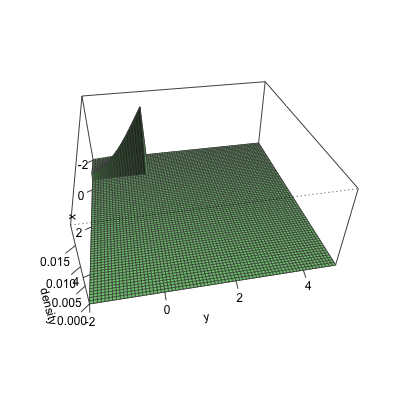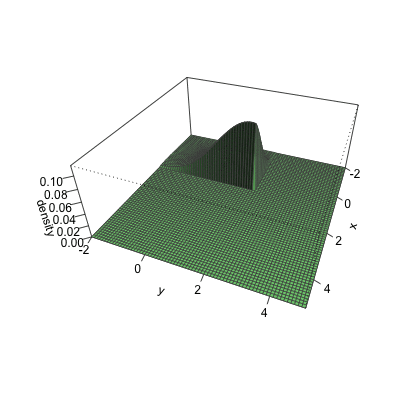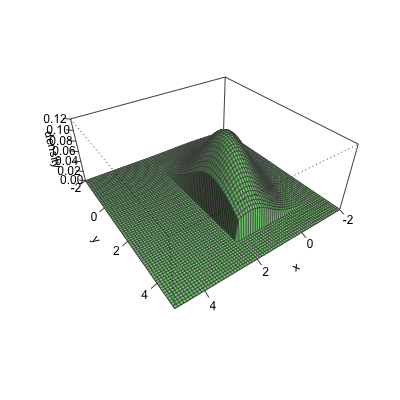
Cumulative distribution using pmvnorm

Bivariate CDF at x = 2 and y = 4 for a normal with ${\mu}={\begin{pmatrix} 1 \\ 2 \end{pmatrix}},\quad { \Sigma }={\begin{pmatrix} 1 & 0.5 \\ 0.5 & 2 \end{pmatrix}}$

mu1 <- c(1, 2)
sigma1 <- matrix(c(1, 0.5, 0.5, 2), 2)

pmvnorm(upper = c(2, 4), mean = mu1, sigma = sigma1)

[1] 0.79
attr(,"error")
[1] 1e-15
attr(,"msg")
[1] "Normal Completion"

Probability between two values using pmvnorm

Probability of $ 1 < x <2$ and $2 < y < 4$

pmvnorm(lower = c(1, 2), 
          upper = c(2, 4), 
             mean = mu1, 
              sigma = sigma1)

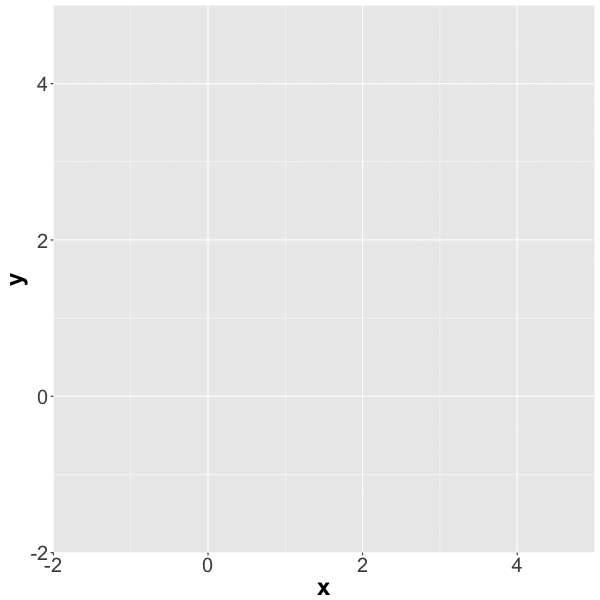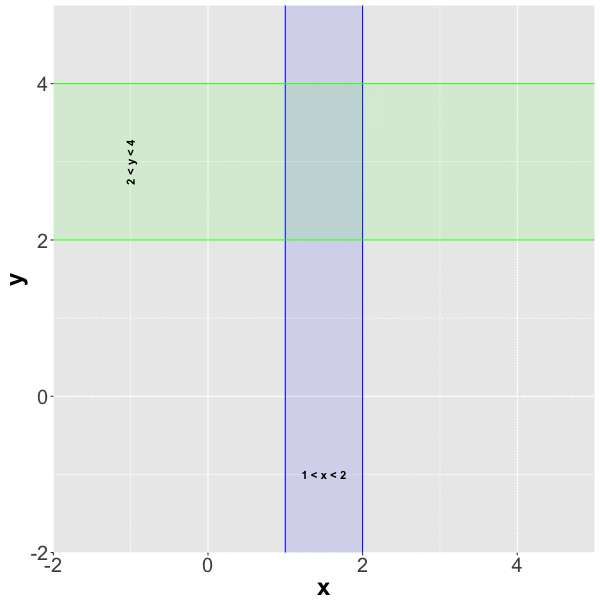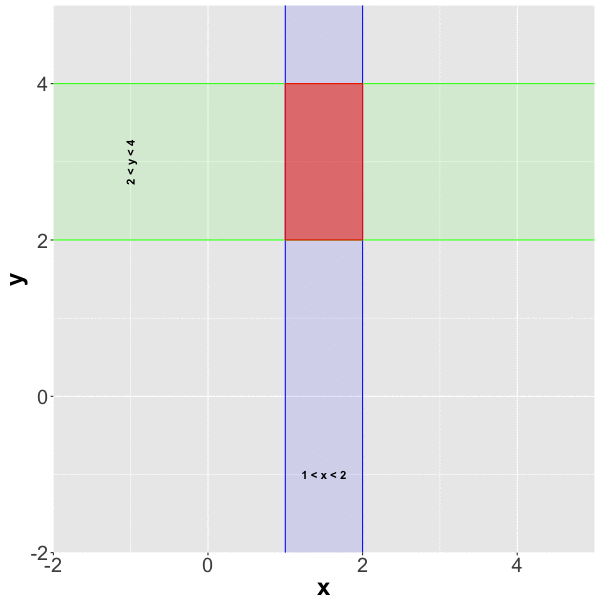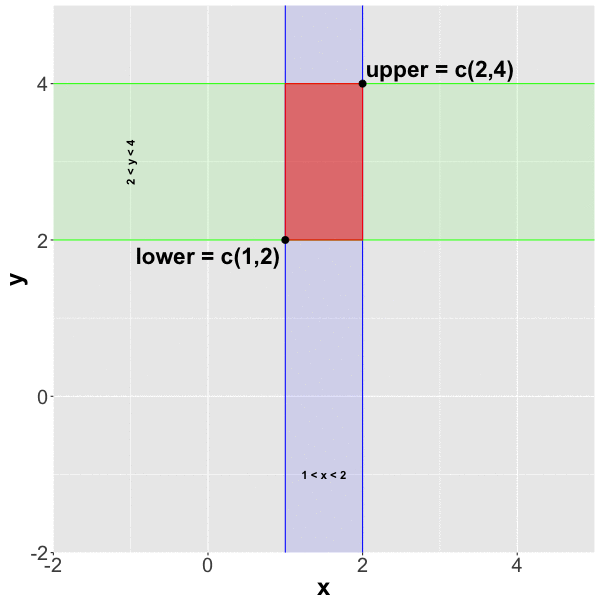
Probability between two values using pmvnorm

Probability of $ 1 < x <2$ and $2 < y < 4$

pmvnorm(lower = c(1, 2), 
          upper = c(2, 4), 
             mean = mu1, 
              sigma = sigma1)

[1] 0.163

Inverse CDF for bivariate normal

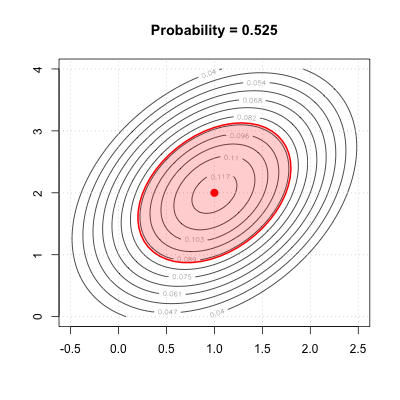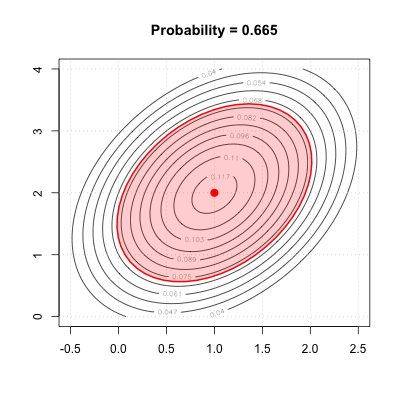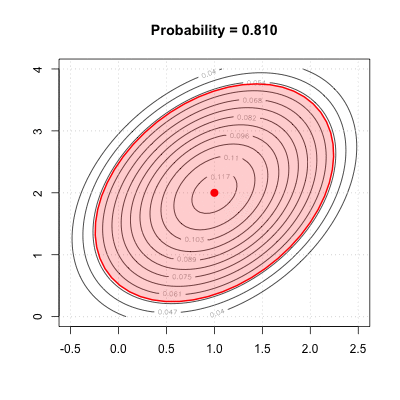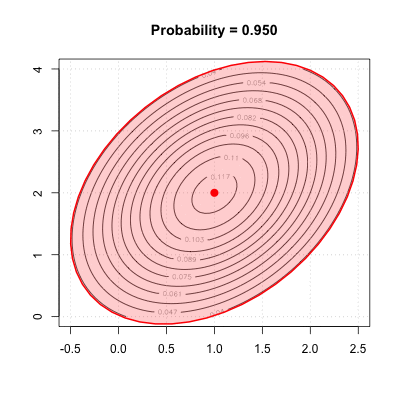Dark red ellipse is the 0.95 quantile

qmvnorm

Implementing qmvnorm to calculate quantiles

sigma1 <- diag(2)
sigma1

     [,1] [,2]
[1,]    1    0
[2,]    0    1

qmvnorm(p = 0.95, sigma = sigma1, tail = "both")

$quantile
[1] 2.24
$f.quantile
[1] -1.31e-06
attr(,"message")
[1] "Normal Completion"

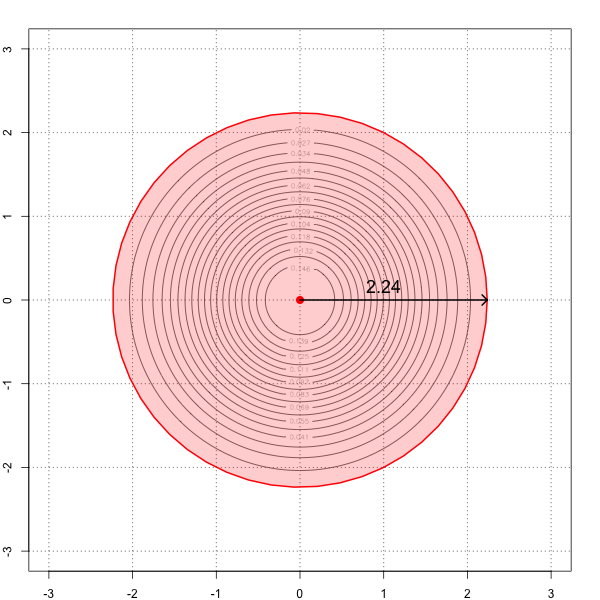
The red circle with radius 2.24 contains 0.95 of the probability

Let's practice!

Multivariate Probability Distributions in R