Choosing the number of components

Multivariate Probability Distributions in R

Surajit Ray

Professor, University of Glasgow

Summary of princomp object

summary(cars.pca)

Importance of components:
                       Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8  Comp.9
Standard deviation      2.378  1.443  0.710 0.5148 0.4280 0.3518 0.3241 0.2419 0.14896
Proportion of Variance  0.628  0.231  0.056 0.0294 0.0204 0.0138 0.0117 0.0065 0.00247
Cumulative Proportion   0.628  0.860  0.916 0.9453 0.9656 0.9794 0.9910 0.9975 1.00000

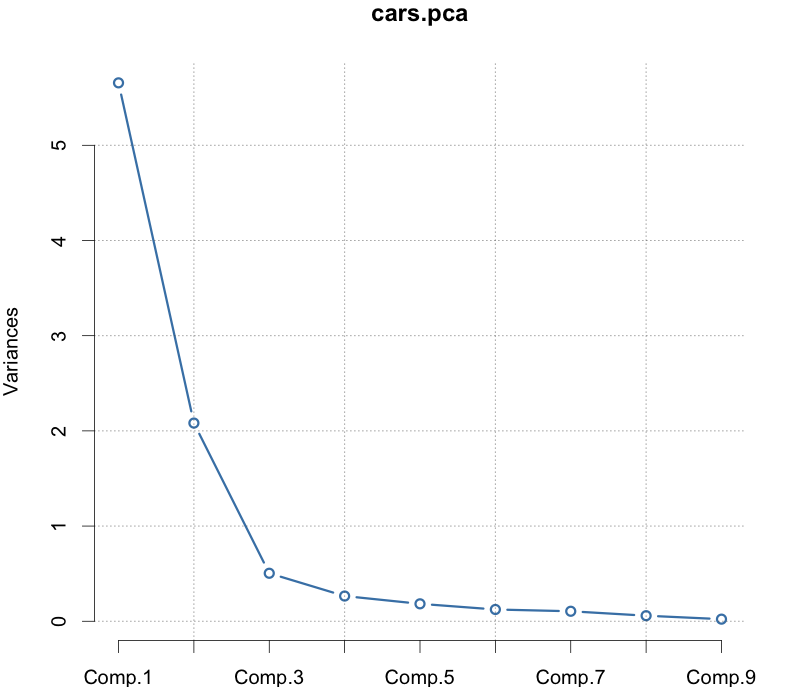
Using the scree plot

Method 1

Proportion of variation explained

screeplot(cars.pca, type = "lines")

Choice based on

steepness of curve
followed by a flat line

Cumulative variance explained

Method 2

Cumulative variation
Explain predetermined value

summary(cars.pca)

Importance of components:
                      Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8  Comp.9
Standard deviation     2.378  1.443  0.710 0.5148 0.4280 0.3518 0.3241 0.2419 0.14896
Proportion of Variance 0.628  0.231  0.056 0.0294 0.0204 0.0138 0.0117 0.0065 0.00247
Cumulative Proportion  0.628  0.860  0.916 0.9453 0.9656 0.9794 0.9910 0.9975 1.00000

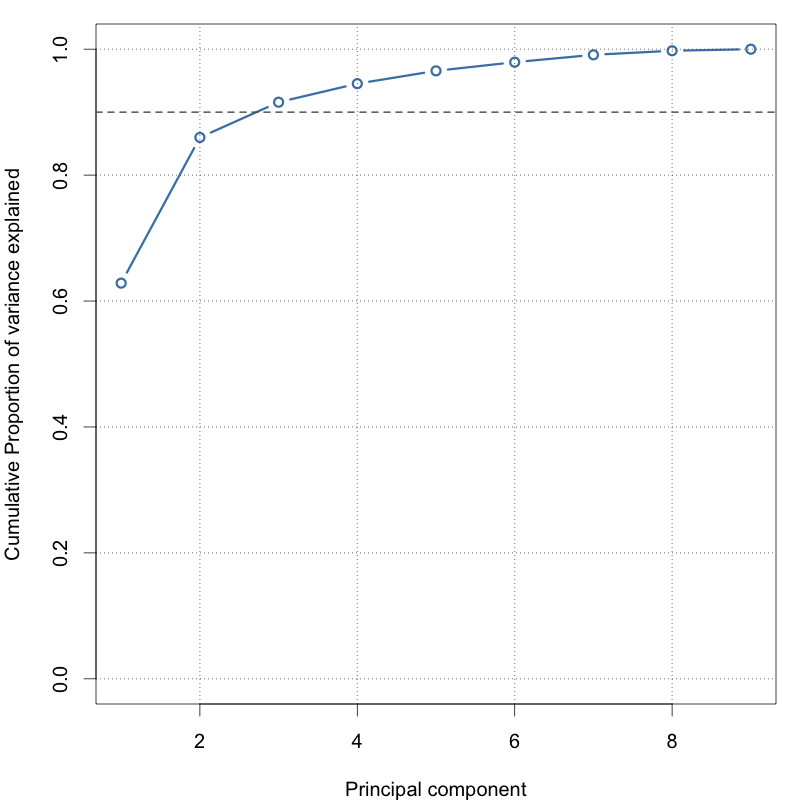
Calculating cumulative proportional variance

Cumulative proportion

# Variance explained
pc.var <- cars.pca$sdev^2

# Proportion of variation
pc.pvar <- pc.var / sum(pc.var)

# Cumulative proportion
plot(cumsum(pc.pvar), type = 'b')

abline(h = 0.9, lty = 2)

Calculating cumulative proportional variance

Cumulative proportion

# Variance explained
pc.var <- cars.pca$sdev^2

# Proportion of variation
pc.pvar <- pc.var / sum(pc.var)

# Cumulative proportion
plot(cumsum(pc.pvar), type = 'b')

abline(h = 0.9, lty = 2)

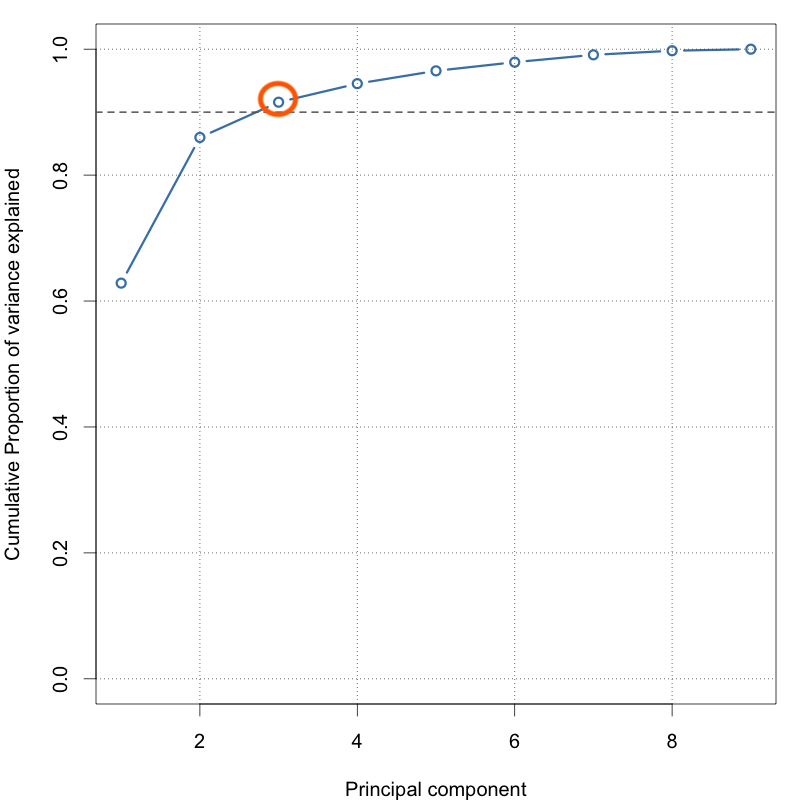
3 PCs explain 90 percent of the variation

Let's practice using these techniques!

Multivariate Probability Distributions in R