Density and cumulative density for multivariate-t

Multivariate Probability Distributions in R

Surajit Ray

Reader, University of Glasgow

Example of multivariate t-distribution

Individual stocks
- Univariate t
Portfolio (3 stocks)
- Multivariate t
Probability that all three stocks between $100-150
- pmvt()
Range of values that the stocks fluctuate 95% of the time
- qmvt()

Density using dmvt

dmvt(x, delta = rep(0, p), sigma = diag(p), log = TRUE)

x can be a vector or a matrix
Unlike dmvnorm the default calculation is in log scale

To get the densities in natural scale use

dmvt(x, delta = rep(0, p), sigma = diag(p), log = FALSE)

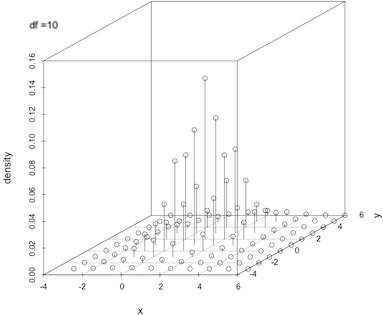
Calculating the density of a multivariate t-distribution on a grid

x <- seq(-3, 6, by = 1); y <- seq(-3, 6, by = 1)
d <- expand.grid(x = x, y = x)                   
del1 <- c(1, 2); sig1 <- matrix(c(1, .5, .5, 2), 2)
dens <- dmvt(as.matrix(d), delta = del1, sigma = sig1, df = 10, log = FALSE)

scatterplot3d(cbind(d, dens), type = "h", zlab = "density")

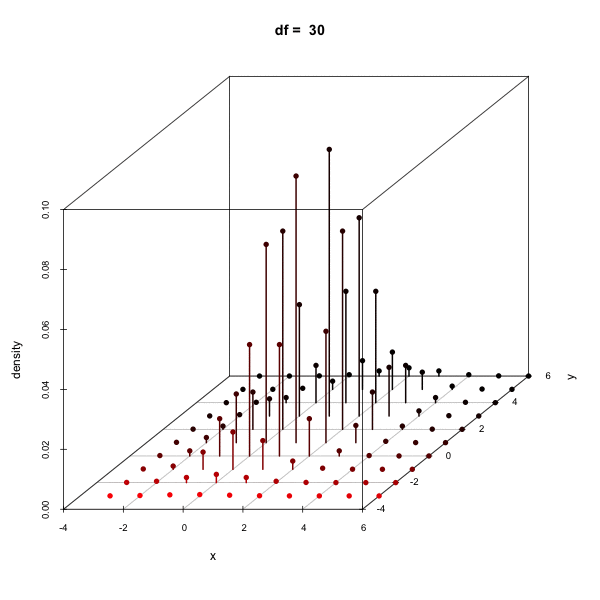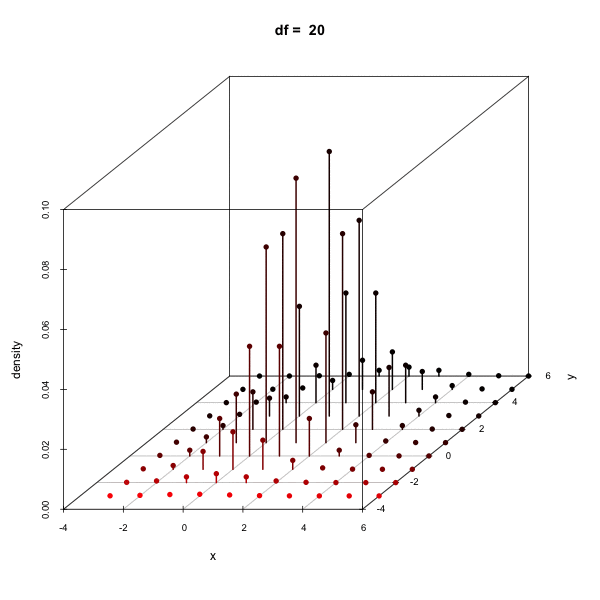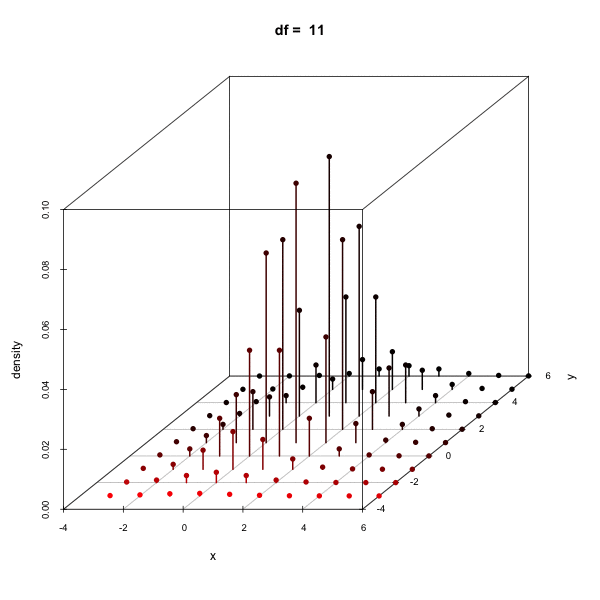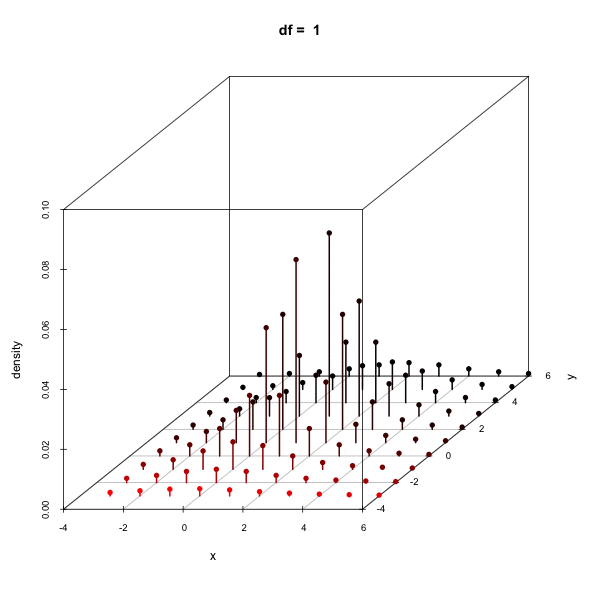
Effect of changing the degees of freedom

Cumulative density using pmvt

pmvt(lower = -Inf, upper = Inf, delta, sigma, df, ...)

Calculates the cdf or volume similar to normal pmvnorm() function

pmvt(lower = c(-1, -2), upper = c(2, 2), delta = c(1, 2), sigma = diag(2), df = 6)

[1] 0.3857
attr(,"error")
[1] 0.0002542
attr(,"msg")
[1] "Normal Completion"

Inverse cdf of t-distribution

qmvt(p, interval, tail, delta, sigma, df)

Computes the quantile of the multivariate t-distribution
Computation techniques similar to qmvnorm() function

Calculate the 0.95 quantile for 3 degrees of freedom

qmvt( p = 0.95, sigma = diag(2), tail = "both", df = 3)

$quantile
[1] 3.96

$f.quantile
[1] -1.05e-06

attr(,"message")
[1] "Normal Completion"

Let's put these functions into practice!

Multivariate Probability Distributions in R