Multivariate normal distribution

Multivariate Probability Distributions in R

Surajit Ray

Professor, University of Glasgow

Univariate normal distribution

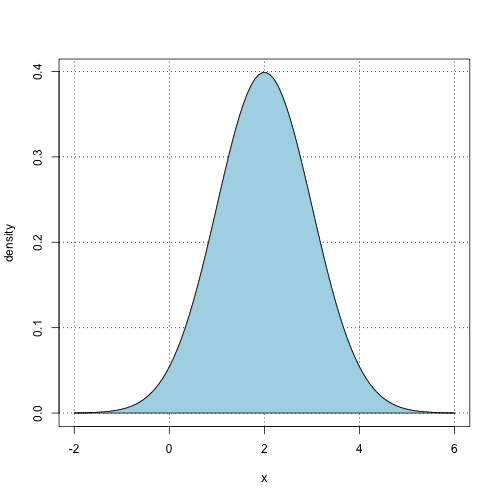Univariate normal with mean 2 and variance 1

Density shape of a bivariate normal animation

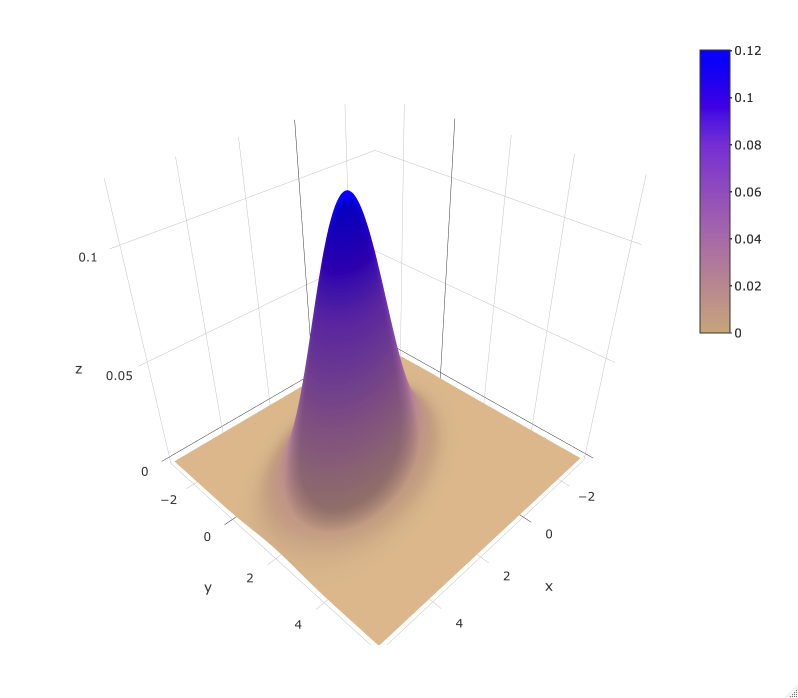
Bivariate normal density - 3D density plot

${\mu}={\begin{pmatrix} 1 \\ 2 \end{pmatrix}},\quad { \Sigma }={\begin{pmatrix} 1 & 0.5 \\ 0.5 & 2 \end{pmatrix}}$

surface

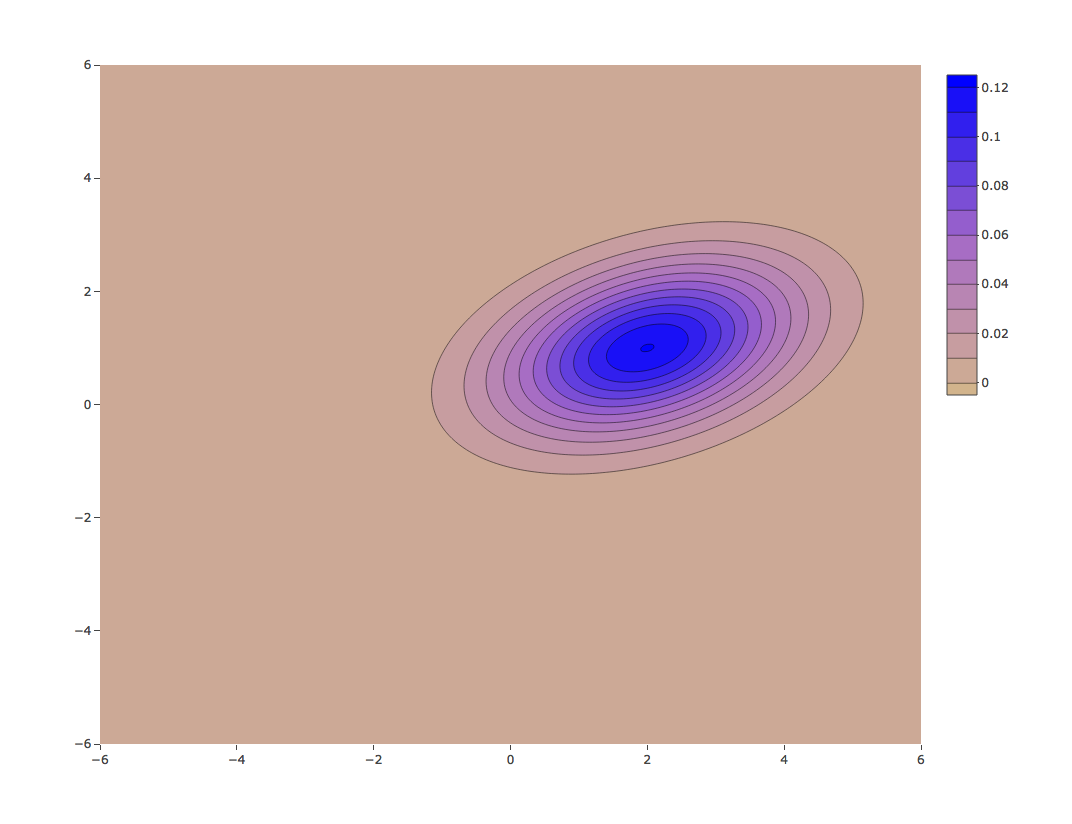
Bivariate normal density - contour plot

${\mu}={\begin{pmatrix} 1 \\ 2 \end{pmatrix}},\quad { \Sigma }={\begin{pmatrix} 1 & 0.5 \\ 0.5 & 2 \end{pmatrix}}$

contour

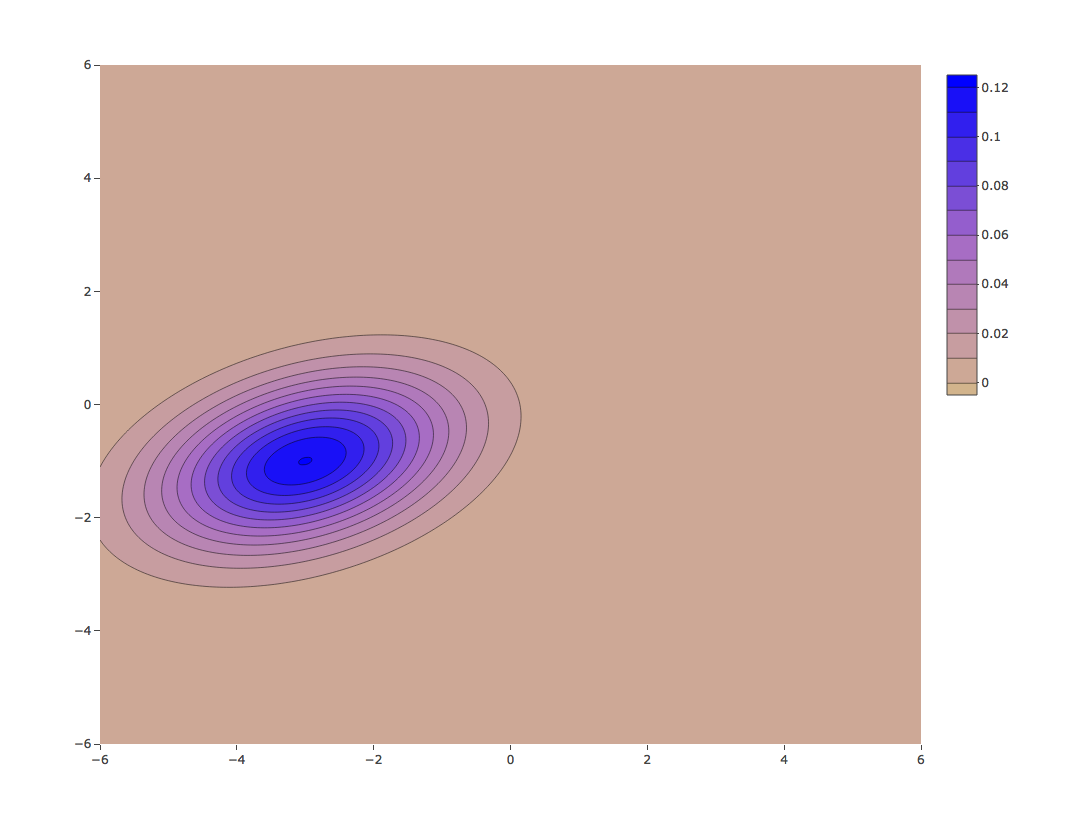
Bivariate normal density with a different mean

${\mu}={\begin{pmatrix} -1 \\ -3 \end{pmatrix}},\quad { \Sigma }={\begin{pmatrix} 1 & 0.5 \\ 0.5 & 2 \end{pmatrix}}$

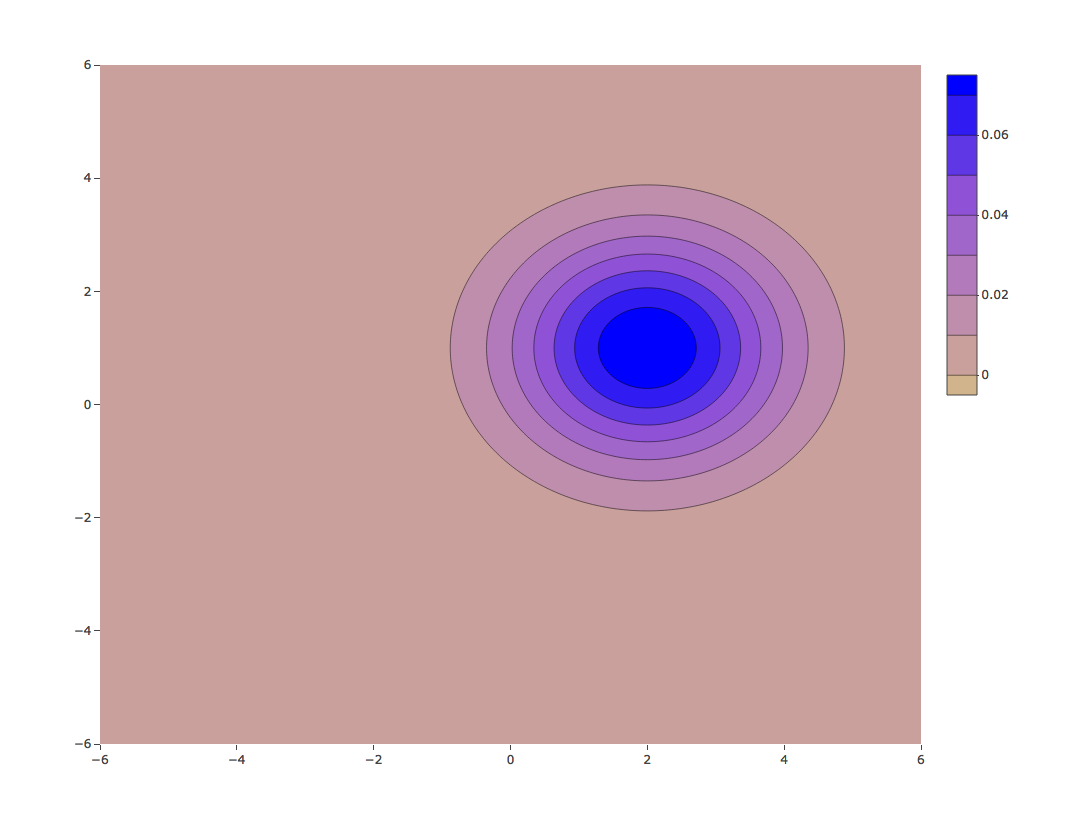
Bivariate normal density with a different variance

${\mu}={\begin{pmatrix}\phantom{-}1 \\\phantom{-}2 \end{pmatrix}} ,\quad { \Sigma }={\begin{pmatrix}2 & 0 \\ 0 & 2 \end{pmatrix}}$

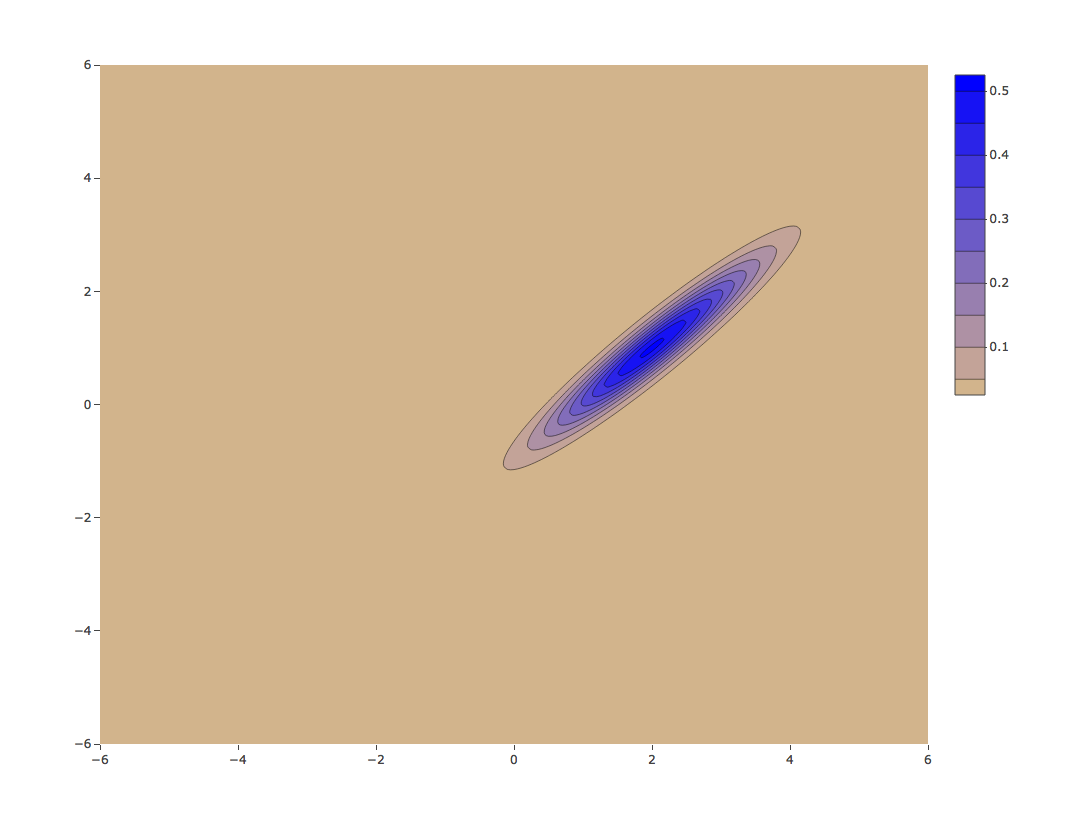
Bivariate normal density with strong correlation

${\mu}={\begin{pmatrix}\phantom{-}1 \\\phantom{-}2 \end{pmatrix}},\quad { \Sigma }={\begin{pmatrix}1& 0.95 \\0.95 & 1 \end{pmatrix}}$

Functions for statistical distributions in R

The first letter denotes
- p for "probability"
- q for "quantile"
- d for "density"
- r for "random"

The rmvnorm function

library(mvtnorm)
rmvnorm(n, mean , sigma)

Need to specify:

n the number of samples
mean the mean of the distribution
sigma the variance-covariance matrix

Using rmvnorm to generate random samples

Generate 1000 samples from a 3 dimensional normal with

$$ \mu= \begin{pmatrix} 1 \\ 2 \\ -5 \end{pmatrix} \Sigma={\begin{pmatrix} 1 & 1 & 0 \\ 1 & 2 & 0 \\ 0 & 0 & 5 \end{pmatrix}} $$

mu1 <- c(1, 2, -5) 
sigma1 <- matrix(c(1,1,0,
                  1,2,0,
                  0,0,5),3,3)
set.seed(34)                  
rmvnorm(n = 1000, mean = mu1, sigma = sigma1)

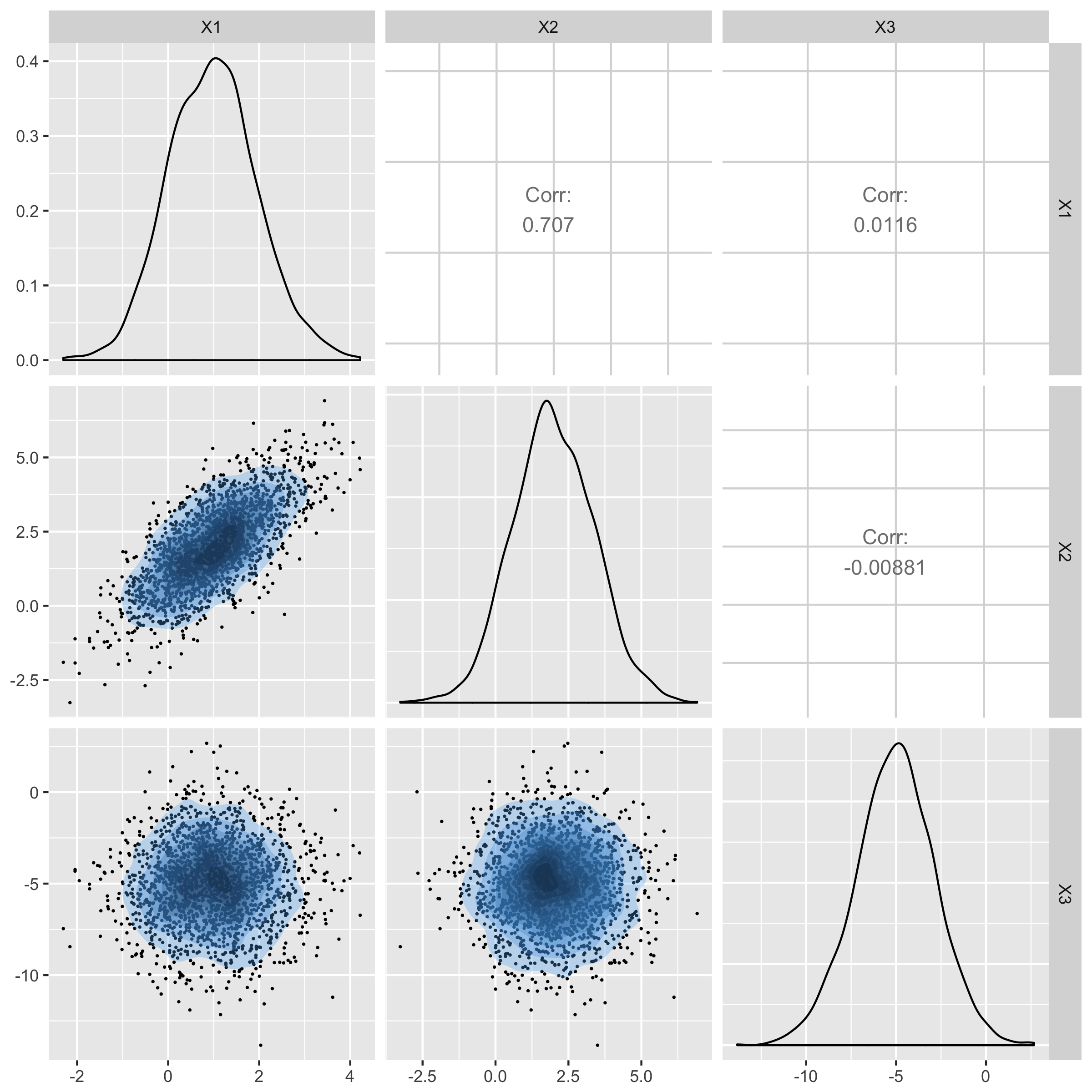
Plot of generated samples simulation

Let's practice simulating from a multivariate normal distribution!

Multivariate Probability Distributions in R