More complex modeling
Analyzing Survey Data in R

Kelly McConville
Assistant Professor of Statistics
Multiple linear regression
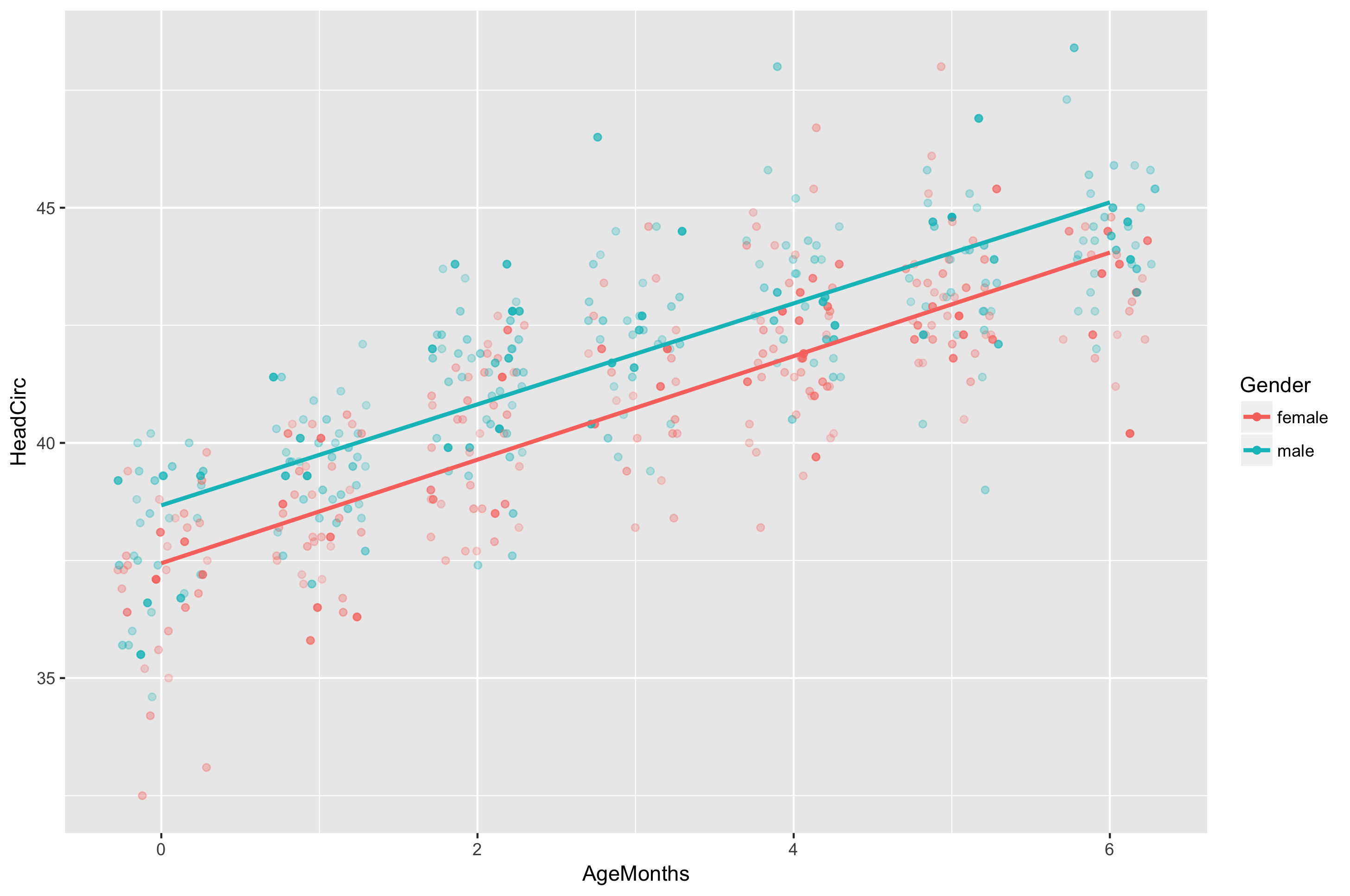
Multiple linear regression
- Multiple linear regression equation is given by:
$$E(y) = B_0 + B_1 x_1 + B_2x_2 + \ldots + B_p x_p$$
babies
# A tibble: 484 x 4
AgeMonths HeadCirc WTMEC4YR Gender
<int> <dbl> <dbl> <fct>
1 3 42.7 12915. male
2 4 42.8 12791. female
3 2 38.8 2359. female
4 0 36.0 4306. female
5 5 42.7 2922. female
6 2 41.9 5561. male
7 6 44.3 10416. female
# ... with 477 more rows
Multiple linear regression
- Multiple linear regression equation is given by:
$$E(y) = B_0 + B_1 x_1 + B_2x_2$$
babies
# A tibble: 484 x 4
AgeMonths HeadCirc WTMEC4YR Gender
<int> <dbl> <dbl> <fct>
1 3 42.7 12915. male
2 4 42.8 12791. female
3 2 38.8 2359. female
4 0 36.0 4306. female
5 5 42.7 2922. female
6 2 41.9 5561. male
7 6 44.3 10416. female
# ... with 477 more rows
Multiple linear regression
babies <- mutate(babies, Gender2 = case_when(
Gender == "male" ~ 1,
Gender == "female" ~ 0))
babies
# A tibble: 484 x 5
AgeMonths HeadCirc WTMEC4YR Gender Gender2
<int> <dbl> <dbl> <fct> <dbl>
1 3 42.7 12915. male 1.
2 4 42.8 12791. female 0.
3 2 38.8 2359. female 0.
4 0 36.0 4306. female 0.
5 5 42.7 2922. female 0.
6 2 41.9 5561. male 1.
7 6 44.3 10416. female 0.
# ... with 477 more rows
Multiple linear regression
- Multiple linear regression equation is given by:
$$E(y) = B_0 + B_1 x_1 + B_2x_2$$
- Line for males:
$$E(y) = (B_0 + B_2) + B_1 x_1$$
- Line for females:
$$E(y) = B_0 + B_1 x_1$$
Multiple linear regression
mod <- svyglm(HeadCirc ~ AgeMonths + Gender, design = NHANES_design)
summary(mod)
svyglm(formula = HeadCirc ~ AgeMonths + Gender, design = NHANES_design)
Survey design:
svydesign(data = NHANESraw, strata = ~SDMVSTRA, id = ~SDMVPSU,
nest = TRUE, weights = ~WTMEC4YR)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 37.48508 0.18320 204.613 < 2e-16 ***
AgeMonths 1.08658 0.05379 20.200 < 2e-16 ***
Gendermale 1.15034 0.16298 7.058 6.3e-08 ***
(Some output omitted)
Multiple linear regression
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 37.48508 0.18320 204.613 < 2e-16 ***
AgeMonths 1.08658 0.05379 20.200 < 2e-16 ***
Gendermale 1.15034 0.16298 7.058 6.3e-08 ***
(Some output omitted)
Null hypothesis: Given age is in the model, gender should not be included ($B_2 = 0$).
Alternative hypothesis: Given age is in the model, gender should be included ($B_2 \neq 0$).
Test statistic: $t = \frac{b_2}{SE}$
Multiple linear regression
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 37.48508 0.18320 204.613 < 2e-16 ***
AgeMonths 1.08658 0.05379 20.200 < 2e-16 ***
Gendermale 1.15034 0.16298 7.058 6.3e-08 ***
(Some output omitted)
Null hypothesis: Given gender is in the model, age should not be included ($B_1 = 0$).
Alternative hypothesis: Given gender is in the model, age should be included ($B_1 \neq 0$).
Test statistic: $t = \frac{b_1}{SE}$
Multiple linear regression
$$E(y) = B_0 + B_1 x_1 + B_2x_2$$

Let's practice!
Analyzing Survey Data in R

